- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2001 AMC12真题及答案详细解析
2001 AMC 12 真题
答案详细解析请参考文末
Problem 1
The sum of two numbers is ![]() . Suppose
. Suppose ![]() is added to each number and then each of the resulting numbers is doubled. What is the sum of the final two numbers?
is added to each number and then each of the resulting numbers is doubled. What is the sum of the final two numbers?
![]()
Problem 2
Let ![]() and
and ![]() denote the product and the sum, respectively, of the digits of the integer
denote the product and the sum, respectively, of the digits of the integer ![]() . For example,
. For example, ![]() and
and ![]() . Suppose
. Suppose ![]() is a two-digit number such that
is a two-digit number such that ![]() . What is the units digit of
. What is the units digit of ![]() ?
?
![]()
Problem 3
The state income tax where Kristin lives is levied at the rate of ![]() of the first
of the first ![]() of annual income plus
of annual income plus ![]() of any amount above
of any amount above ![]() . Kristin noticed that the state income tax she paid amounted to
. Kristin noticed that the state income tax she paid amounted to ![]() of her annual income. What was her annual income?
of her annual income. What was her annual income?
![]()
Problem 4
The mean of three numbers is ![]() more than the least of the numbers and
more than the least of the numbers and ![]() less than the greatest. The median of the three numbers is
less than the greatest. The median of the three numbers is ![]() . What is their sum?
. What is their sum?
![]()
Problem 5
What is the product of all positive odd integers less than 10000?
![]()
Problem 6
A telephone number has the form ![]() , where each letter represents a different digit. The digits in each part of the number are in decreasing order; that is,
, where each letter represents a different digit. The digits in each part of the number are in decreasing order; that is, ![]() ,
, ![]() , and
, and ![]() . Furthermore,
. Furthermore, ![]() ,
, ![]() , and
, and ![]() are consecutive even digits;
are consecutive even digits; ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are consecutive odd digits; and
are consecutive odd digits; and ![]() . Find
. Find ![]() .
.
![]()
Problem 7
A charity sells ![]() benefit tickets for a total of
benefit tickets for a total of ![]() . Some tickets sell for full price (a whole dollar amount), and the rest sells for half price. How much money is raised by the full-price tickets?
. Some tickets sell for full price (a whole dollar amount), and the rest sells for half price. How much money is raised by the full-price tickets?
![]()
Problem 8
Which of the cones listed below can be formed from a ![]() sector of a circle of radius
sector of a circle of radius ![]() by aligning the two straight sides?
by aligning the two straight sides?
![[asy] import graph; unitsize(1.5cm); defaultpen(fontsize(8pt)); draw(Arc((0,0),1,-72,180),linewidth(.8pt)); draw(dir(288)--(0,0)--(-1,0),linewidth(.8pt)); label("$10$",(-0.5,0),S); draw(Arc((0,0),0.1,-72,180)); label("$252^{circ}$",(0.05,0.05),NE); [/asy]](https://latex.artofproblemsolving.com/b/b/8/bb8af0c17ff35be1e553d36477a23ce3f026bded.png)
![]()
![]()
![]()
![]()
![]()
Problem 9
Let ![]() be a function satisfying
be a function satisfying ![]() for all positive real numbers
for all positive real numbers ![]() and
and ![]() . If
. If ![]() , what is the value of
, what is the value of ![]() ?
?
![]()
Problem 10
The plane is tiled by congruent squares and congruent pentagons as indicated. The percent of the plane that is enclosed by the pentagons is closest to
![]()
![[asy] unitsize(3mm); defaultpen(linewidth(0.8pt)); path p1=(0,0)--(3,0)--(3,3)--(0,3)--(0,0); path p2=(0,1)--(1,1)--(1,0); path p3=(2,0)--(2,1)--(3,1); path p4=(3,2)--(2,2)--(2,3); path p5=(1,3)--(1,2)--(0,2); path p6=(1,1)--(2,2); path p7=(2,1)--(1,2); path[] p=p1^^p2^^p3^^p4^^p5^^p6^^p7; for(int i=0; i<3; ++i) { for(int j=0; j<3; ++j) { draw(shift(3*i,3*j)*p); } } [/asy]](https://latex.artofproblemsolving.com/2/c/8/2c8743395e4a086d2ae9a30a2d161157e7dc3077.png)
Problem 11
A box contains exactly five chips, three red and two white. Chips are randomly removed one at a time without replacement until all the red chips are drawn or all the white chips are drawn. What is the probability that the last chip drawn is white?
![]()
Problem 12
How many positive integers not exceeding ![]() are multiples of
are multiples of ![]() or
or ![]() but not
but not ![]() ?
?
![]()
Problem 13
The parabola with equation ![]() and vertex
and vertex ![]() is reflected about the line
is reflected about the line ![]() . This results in the parabola with equation
. This results in the parabola with equation ![]() . Which of the following equals
. Which of the following equals ![]() ?
?
![]()
Problem 14
Given the nine-sided regular polygon ![]() , how many distinct equilateral triangles in the plane of the polygon have at least two vertices in the set
, how many distinct equilateral triangles in the plane of the polygon have at least two vertices in the set ![]() ?
?
![]()
Problem 15
An insect lives on the surface of a regular tetrahedron with edges of length 1. It wishes to travel on the surface of the tetrahedron from the midpoint of one edge to the midpoint of the opposite edge. What is the length of the shortest such trip? (Note: Two edges of a tetrahedron are opposite if they have no common endpoint.)
![]()
Problem 16
A spider has one sock and one shoe for each of its eight legs. In how many different orders can the spider put on its socks and shoes, assuming that, on each leg, the sock must be put on before the shoe?
![]()
Problem 17
A point ![]() is selected at random from the interior of the pentagon with vertices
is selected at random from the interior of the pentagon with vertices ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . What is the probability that
. What is the probability that ![]() is obtuse?
is obtuse?
![]()
Problem 18
A circle centered at ![]() with a radius of 1 and a circle centered at
with a radius of 1 and a circle centered at ![]() with a radius of 4 are externally tangent. A third circle is tangent to the first two and to one of their common external tangents as shown. The radius of the third circle is
with a radius of 4 are externally tangent. A third circle is tangent to the first two and to one of their common external tangents as shown. The radius of the third circle is
![[asy] unitsize(0.75cm); pair A=(0,1), B=(4,4); dot(A); dot(B); draw( circle(A,1) ); draw( circle(B,4) ); draw( (-1.5,0)--(8.5,0) ); draw( A -- (A+(-1,0)) ); label("$1$", A -- (A+(-1,0)), N ); draw( B -- (B+(4,0)) ); label("$4$", B -- (B+(4,0)), N ); label("$A$",A,E); label("$B$",B,W); filldraw( circle( (12/9,4/9), 4/9 ), lightgray, black ); dot( (12/9,4/9) ); [/asy]](https://latex.artofproblemsolving.com/e/0/3/e0340e3581aab9d635bcf2dca6b71152f8fa5290.png)
![]()
Problem 19
The polynomial ![]() has the property that the mean of its zeros, the product of its zeros, and the sum of its coefficients are all equal. If the
has the property that the mean of its zeros, the product of its zeros, and the sum of its coefficients are all equal. If the ![]() -intercept of the graph of
-intercept of the graph of ![]() is 2, what is
is 2, what is ![]() ?
?
![]()
Problem 20
Points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() lie in the first quadrant and are the vertices of quadrilateral
lie in the first quadrant and are the vertices of quadrilateral ![]() . The quadrilateral formed by joining the midpoints of
. The quadrilateral formed by joining the midpoints of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() is a square. What is the sum of the coordinates of point
is a square. What is the sum of the coordinates of point ![]() ?
?
![]()
Problem 21
Four positive integers ![]() ,
, ![]() ,
, ![]() , and
, and ![]() have a product of
have a product of ![]() and satisfy:
and satisfy:

What is ![]() ?
?
![]()
Problem 22
In rectangle ![]() , points
, points ![]() and
and ![]() lie on
lie on ![]() so that
so that ![]() and
and ![]() is the midpoint of
is the midpoint of ![]() . Also,
. Also, ![]() intersects
intersects ![]() at
at ![]() and
and ![]() at
at ![]() . The area of the rectangle
. The area of the rectangle ![]() is
is ![]() . Find the area of triangle
. Find the area of triangle ![]() .
.
![]()
Problem 23
A polynomial of degree four with leading coefficient 1 and integer coefficients has two real zeros, both of which are integers. Which of the following can also be a zero of the polynomial?
![]()
Problem 24
In ![]() ,
, ![]() . Point
. Point ![]() is on
is on ![]() so that
so that ![]() and
and ![]() . Find
. Find ![]() .
.
![]()
Problem 25
Consider sequences of positive real numbers of the form ![]() in which every term after the first is 1 less than the product of its two immediate neighbors. For how many different values of
in which every term after the first is 1 less than the product of its two immediate neighbors. For how many different values of ![]() does the term 2001 appear somewhere in the sequence?
does the term 2001 appear somewhere in the sequence?
![]()
2001 AMC12 真题答案详细解析
- Suppose the two numbers are
 and
and  , with
, with  . Then the desired sum is
. Then the desired sum is  , which is answer
, which is answer  .
. - Denote
 and
and  as the tens and units digit of
as the tens and units digit of  , respectively. Then
, respectively. Then  . It follows that
. It follows that  , which implies that
, which implies that  . Since
. Since  ,
,  . So the units digit of
. So the units digit of  is
is  .
. -
Solution 1
Let the income amount be denoted by
 .
.We know that
 .
.We can now try to solve for
 :
:


So the answer is

Solution 2
Let
 ,
,  be Kristin's annual income and the income tax total, respectively. Notice that
be Kristin's annual income and the income tax total, respectively. Notice that![begin{align*} T &= p%cdot28000 + (p + 2)%cdot(A - 28000) \ &= [p%cdot28000 + p%cdot(A - 28000)] + 2%cdot(A - 28000) \ &= p%cdot A + 2%cdot(A - 28000) end{align*}](https://latex.artofproblemsolving.com/a/3/9/a394ead7d83dc9889466a806e206ea2bbdcc9545.png) We are also given that
We are also given that![[T = (p + 0.25)%cdot A = p%cdot A + 0.25%cdot A]](https://latex.artofproblemsolving.com/7/5/4/75405b5351821fc58d14290fd4dddf42a77ec4da.png) Thus,
Thus,![[p%cdot A + 2%cdot(A - 28000) = p%cdot A + 0.25%cdot A]](https://latex.artofproblemsolving.com/6/f/b/6fb9c5d80e3f1733bd16e4837f9bcbeb5a8e7150.png)
![[2%cdot(A - 28000) = 0.25%cdot A]](https://latex.artofproblemsolving.com/d/1/0/d1025839a18cab02a12511105eb85edae3851ec6.png) Solve for
Solve for  to obtain
to obtain  .
. 
- Let
 be the mean of the three numbers. Then the least of the numbers is
be the mean of the three numbers. Then the least of the numbers is  and the greatest is
and the greatest is  . The middle of the three numbers is the median, 5. So
. The middle of the three numbers is the median, 5. So ![$dfrac{1}{3}[(m-10) + 5 + (m + 15)] = m$](https://latex.artofproblemsolving.com/c/a/c/cac4efd76d95dce2367e45a25811bc7142c1a3b8.png) , which implies that
, which implies that  . Hence, the sum of the three numbers is
. Hence, the sum of the three numbers is  .
. 

- The last four digits
 are either
are either  or
or  , and the other odd digit (
, and the other odd digit ( or
or  ) must be
) must be  ,
, 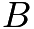 , or
, or  . Since
. Since  , that digit must be
, that digit must be  . Thus the sum of the two even digits in
. Thus the sum of the two even digits in  is
is  .
.  must be
must be  ,
,  , or
, or  , which respectively leave the pairs
, which respectively leave the pairs  and
and  ,
,  and
and  , or
, or  and
and  , as the two even digits in
, as the two even digits in  . Only
. Only  and
and  has sum
has sum  , so
, so  is
is  , and the required first digit is
, and the required first digit is  .
. -
Solution 1
Let's multiply ticket costs by
 , then the half price becomes an integer, and the charity sold
, then the half price becomes an integer, and the charity sold  tickets worth a total of
tickets worth a total of  dollars.
dollars.Let
 be the number of half price tickets, we then have
be the number of half price tickets, we then have  full price tickets. The cost of
full price tickets. The cost of  full price tickets is equal to the cost of
full price tickets is equal to the cost of  half price tickets.
half price tickets.Hence we know that
 half price tickets cost
half price tickets cost  dollars. Then a single half price ticket costs
dollars. Then a single half price ticket costs  dollars, and this must be an integer. Thus
dollars, and this must be an integer. Thus  must be a divisor of
must be a divisor of  . Keeping in mind that
. Keeping in mind that  , we are looking for a divisor between
, we are looking for a divisor between  and
and  , inclusive.
, inclusive.The prime factorization of
 is
is  . We can easily find out that the only divisor of
. We can easily find out that the only divisor of  within the given range is
within the given range is  .
.This gives us
 , hence there were
, hence there were  half price tickets and
half price tickets and  full price tickets.
full price tickets.In our modified setting (with prices multiplied by
 ) the price of a half price ticket is
) the price of a half price ticket is  . In the original setting this is the price of a full price ticket. Hence
. In the original setting this is the price of a full price ticket. Hence  dollars are raised by the full price tickets.
dollars are raised by the full price tickets.Solution 2
Let the cost of the full price ticket be
 , let the number of full price tickets be
, let the number of full price tickets be  and half price tickets be
and half price tickets be 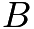
Multiplying everything by two first to make cancel out fractions.
We have

And we have

Plugging in, we get

Simplifying, we get

Factoring out the
 , we get
, we get 
Obviously, we see that the fraction has to simplify to an integer.
Hence,
 has to be a factor of 4002.
has to be a factor of 4002.By inspection, we see that the prime factorization of

We see that
 through inspection. We also find that
through inspection. We also find that 
Hence, the price of full tickets out of
 is
is  .
. ![[asy] import graph; unitsize(1.5cm); defaultpen(fontsize(8pt)); draw(Arc((0,0),1,-72,180),linewidth(.8pt) + red); draw(dir(288)--(0,0)--(-1,0),linewidth(.8pt) + blue); label("$10$",(-0.5,0),S); draw(Arc((0,0),0.1,-72,180)); label("$252^{circ}$",(0.05,0.05),NE); [/asy]](https://latex.artofproblemsolving.com/2/1/f/21ff3c1e4bdeb7eae01918390e3702a2b8ab2a01.png) The blue lines will be joined together to form a single blue line on the surface of the cone, hence
The blue lines will be joined together to form a single blue line on the surface of the cone, hence  will be the
will be the  of the cone.The red line will form the circumference of the base. We can compute its length and use it to determine the radius.The length of the red line is
of the cone.The red line will form the circumference of the base. We can compute its length and use it to determine the radius.The length of the red line is  . This is the circumference of a circle with radius
. This is the circumference of a circle with radius  .Therefore the correct answer is
.Therefore the correct answer is  .
.-
Solution 1
Letting
 and
and  in the given equation, we get
in the given equation, we get  , or
, or  .
.Solution 2
The only function that satisfies the given condition is
 , for some constant
, for some constant  . Thus, the answer is
. Thus, the answer is  .
. - Consider any single tile:
![[asy] unitsize(1cm); defaultpen(linewidth(0.8pt)); path p1=(0,0)--(3,0)--(3,3)--(0,3)--(0,0); path p2=(0,1)--(1,1)--(1,0); path p3=(2,0)--(2,1)--(3,1); path p4=(3,2)--(2,2)--(2,3); path p5=(1,3)--(1,2)--(0,2); path p6=(1,1)--(2,2); path p7=(2,1)--(1,2); path[] p=p1^^p2^^p3^^p4^^p5^^p6^^p7; draw(p); [/asy]](https://latex.artofproblemsolving.com/3/6/f/36f7a20120732a8955c3f77ea0d1e81fc34cc6ea.png) If the side of the small square is
If the side of the small square is  , then the area of the tile is
, then the area of the tile is  , with
, with  covered by squares and
covered by squares and  by pentagons. Hence exactly
by pentagons. Hence exactly  of any tile are covered by pentagons, and therefore pentagons cover
of any tile are covered by pentagons, and therefore pentagons cover  of the plane. When expressed as a percentage, this is
of the plane. When expressed as a percentage, this is  , and the closest integer to this value is
, and the closest integer to this value is  .
. -
Solution 1
Imagine that we draw all the chips in random order, i.e., we do not stop when the last chip of a color is drawn. To draw out all the white chips first, the last chip left must be red, and all previous chips can be drawn in any order. Since there are 3 red chips, the probability that the last chip of the five is red (and so also the probability that the last chip drawn is white) is
 .
.Solution 2
Let's assume we don't stop picking until all of the balls are picked. To satisfy this condition, we have to arrange the letters: W, W, R, R, R such that both R's appear in the first 4. We find the number of ways to arrange the red balls in the first 4 and divide that by the total ways to choose all the balls. The probability of this occurring is

-
Solution 1
Out of the numbers
 to
to  four are divisible by
four are divisible by  and three by
and three by  , counting
, counting  twice. Hence
twice. Hence  out of these
out of these  numbers are multiples of
numbers are multiples of  or
or  .
.The same is obviously true for the numbers
 to
to  for any positive integer
for any positive integer  .
.Hence out of the numbers
 to
to  there are
there are  numbers that are divisible by
numbers that are divisible by  or
or  . Out of these
. Out of these  , the numbers
, the numbers  ,
,  ,
,  ,
,  ,
,  and
and  are divisible by
are divisible by  . Therefore in the set
. Therefore in the set  there are precisely
there are precisely  numbers that satisfy all criteria from the problem statement.
numbers that satisfy all criteria from the problem statement.Again, the same is obviously true for the set
 for any positive integer
for any positive integer  .
.We have
 , hence there are
, hence there are  good numbers among the numbers
good numbers among the numbers  to
to  . At this point we already know that the only answer that is still possible is
. At this point we already know that the only answer that is still possible is  , as we only have
, as we only have  numbers left.
numbers left.By examining the remaining
 by hand we can easily find out that exactly
by hand we can easily find out that exactly  of them match all the criteria, giving us
of them match all the criteria, giving us  good numbers. This is correct.
good numbers. This is correct.Solution 2
We can solve this problem by finding the cases where the number is divisible by
 or
or  , then subtract from the cases where none of those cases divide
, then subtract from the cases where none of those cases divide  . To solve the ways the numbers divide
. To solve the ways the numbers divide  or
or  we find the cases where a number is divisible by
we find the cases where a number is divisible by  and
and  as separate cases. We apply the floor function to every case to get
as separate cases. We apply the floor function to every case to get  ,
,  , and
, and  . The first two floor functions were for calculating the number of individual cases for
. The first two floor functions were for calculating the number of individual cases for  and
and  . The third case was to find any overlapping numbers. The numbers were
. The third case was to find any overlapping numbers. The numbers were  ,
,  , and
, and  , respectively. We add the first two terms and subtract the third to get
, respectively. We add the first two terms and subtract the third to get  . The first case is finished.
. The first case is finished.The second case is more or less the same, except we are applying
 and
and  to
to  . We must find the cases where the first case over counts multiples of five. Utilizing the floor function again on the fractions
. We must find the cases where the first case over counts multiples of five. Utilizing the floor function again on the fractions  ,
,  , and
, and  yields the numbers
yields the numbers  ,
,  , and
, and  . The first two numbers counted all the numbers that were multiples of either four with five or three with five less than
. The first two numbers counted all the numbers that were multiples of either four with five or three with five less than  . The third counted the overlapping cases, which we must subtract from the sum of the first two. We do this to reach
. The third counted the overlapping cases, which we must subtract from the sum of the first two. We do this to reach  . Subtracting this number from the original
. Subtracting this number from the original  numbers procures
numbers procures  .
.Solution 3
First find the number of such numbers between 1 and 2000 (inclusive) and then add one to this result because 2001 is a multiple of 3.
There are
 numbers that are not multiples of
numbers that are not multiples of  .
.  are not multiples of
are not multiples of  or
or  , so
, so  numbers are.
numbers are.
Solution 4
Take a good-sized sample of consecutive integers; for example, the first 25 positive integers. Determine that the numbers 3, 4, 6, 8, 9, 12, 16, 18, 21, and 24 exhibit the properties given in the question. 25 is a divisor of 2000, so there are
 numbers satisfying the given conditions between 1 and 2000. Since 2001 is a multiple of 3, add 1 to 800 to get
numbers satisfying the given conditions between 1 and 2000. Since 2001 is a multiple of 3, add 1 to 800 to get  .
. - We write
 as
as  (this is possible for any parabola). Then the reflection of
(this is possible for any parabola). Then the reflection of  is
is  . Then we find
. Then we find  . Since
. Since  and
and  , we have
, we have  , so the answer is
, so the answer is  .
. - Each of the
 pairs of vertices determines two equilateral triangles, one on each side of the segment. This would give us
pairs of vertices determines two equilateral triangles, one on each side of the segment. This would give us  triangles. However, note that there are three equilateral triangles that have all three vertices among the vertices of the polygon. These are the triangles
triangles. However, note that there are three equilateral triangles that have all three vertices among the vertices of the polygon. These are the triangles  ,
,  , and
, and  . We counted each of these three times (once for each side). Hence we overcounted by
. We counted each of these three times (once for each side). Hence we overcounted by  for each of these triangles for a total of
for each of these triangles for a total of  overcounted, and the correct number of equilateral triangles is
overcounted, and the correct number of equilateral triangles is  .
. - Given any path on the surface, we can unfold the surface into a plane to get a path of the same length in the plane. Consider the net of a tetrahedron in the picture below. A pair of opposite points is marked by dots. It is obvious that in the plane the shortest path is just a segment that connects these two points. Its length is the same as the length of the tetrahedron's edge, i.e.
 .
.![[asy] unitsize(2cm); defaultpen(0.8); pair A=(0,0), B=(1,0), C=rotate(60)*B, D1=B+C-A, D2=A+C-B, D3=A+B-C; draw(A--B--C--cycle); draw(D1--B--C--cycle); draw(D2--A--C--cycle); draw(D3--B--A--cycle); dot( A+0.5*(C-A) ); dot( B+0.5*(C-A) ); draw( ( A+0.5*(C-A) ) -- ( B+0.5*(C-A) ), dashed ); [/asy]](https://latex.artofproblemsolving.com/f/2/d/f2d84548c68b8c26bea559248ac713844ce32e42.png)
-
Solution 1
Let the spider try to put on all
 things in a random order. Each of the
things in a random order. Each of the  permutations is equally probable. For any fixed leg, the probability that he will first put on the sock and only then the shoe is clearly
permutations is equally probable. For any fixed leg, the probability that he will first put on the sock and only then the shoe is clearly  . Then the probability that he will correctly put things on all legs is
. Then the probability that he will correctly put things on all legs is  . Therefore the number of correct permutations must be
. Therefore the number of correct permutations must be  .
.Solution 2
Each dressing sequence can be uniquely described by a sequence containing two
 s, two
s, two  s, ..., and two
s, ..., and two  s -- the first occurrence of number
s -- the first occurrence of number  means that the spider puts the sock onto leg
means that the spider puts the sock onto leg  , the second occurrence of
, the second occurrence of  means he puts the shoe onto leg
means he puts the shoe onto leg  . If the numbers were all unique, the answer would be
. If the numbers were all unique, the answer would be  . However, since 8 terms appear twice, the answer is
. However, since 8 terms appear twice, the answer is  .
.Solution 3
You can put all
 socks on first for
socks on first for  ways and then all
ways and then all  shoes on next for
shoes on next for  more ways. This is not the only possibility, so the lower bound is
more ways. This is not the only possibility, so the lower bound is  . You can choose all
. You can choose all  in a random fashion, but some combinations would violate the rules, so the upper bound is
in a random fashion, but some combinations would violate the rules, so the upper bound is  .
.  &
&  are the lower and upper bounds, so the answer is in between them,
are the lower and upper bounds, so the answer is in between them,  .
. - The angle
 is obtuse if and only if
is obtuse if and only if  lies inside the circle with diameter
lies inside the circle with diameter  . (This follows for example from the fact that the inscribed angle is half of the central angle for the same arc.)
. (This follows for example from the fact that the inscribed angle is half of the central angle for the same arc.)![[asy] defaultpen(0.8); real pi=3.14159265359; pair A=(0,2), B=(4,0), C=(2*pi+1, 0), D=(2*pi+1,4), E=(0,4), F=(0,0); draw(A--B--C--D--E--cycle); draw(circle((A+B)/2,length(B-A)/2)); label("$A$",A,W); label("$B$",B,SE); label("$C$",C,SE); label("$D$",D,NE); label("$E$",E,NW); label("$F$",F,SW); draw(A--F--B,dashed); [/asy]](https://latex.artofproblemsolving.com/8/0/4/804c6c9cbc7e5dd38b978d4187e323b7ff360fc4.png) The area of
The area of  is
is ![$[AFB] = frac {AFcdot FB}2 = 4$](https://latex.artofproblemsolving.com/a/5/5/a5590186ab4c4a02dfa423afb635838a064b68ce.png) , and the area of
, and the area of  is
is ![$CDcdot DE - [AFB] = 4cdot (2pi+1) - 4 = 8pi$](https://latex.artofproblemsolving.com/2/f/7/2f7bbcd8826bf9447fd2299c2411e9349a695b5d.png) .From the Pythagorean theorem the length of
.From the Pythagorean theorem the length of  is
is  , thus the radius of the circle is
, thus the radius of the circle is  , and the area of the half-circle that is inside
, and the area of the half-circle that is inside  is
is  .Therefore the probability that
.Therefore the probability that  is obtuse is
is obtuse is  .
. -
Solution 1
![[asy] unitsize(1cm); pair A=(0,1), B=(4,4), C=(4,1), S=(12/9,4/9); dot(A); dot(B); draw( circle(A,1) ); draw( circle(B,4) ); draw( (-1.5,0)--(8.5,0) ); draw( (A+(4,0)) -- A -- (A+(0,-1)) ); draw( A -- B -- (B+(0,-4)) ); label("$A$",A,N); label("$B$",B,N); label("$C$",C,E); label("$S$",S,N); filldraw( circle(S,4/9), lightgray, black ); dot(S); draw( rightanglemark(A,C,B) ); draw( S -- A ); draw( S -- B ); [/asy]](https://latex.artofproblemsolving.com/7/7/f/77ff0006500e55413b38636a2c80caba13c7591d.png)
In the triangle
 we have
we have  and
and  , thus by the Pythagorean theorem we have
, thus by the Pythagorean theorem we have  .
.We can now pick a coordinate system where the common tangent is the
 axis and
axis and  lies on the
lies on the  axis. In this coordinate system we have
axis. In this coordinate system we have  and
and  .
.Let
 be the radius of the small circle, and let
be the radius of the small circle, and let  be the
be the  -coordinate of its center
-coordinate of its center  . We then know that
. We then know that  , as the circle is tangent to the
, as the circle is tangent to the  axis. Moreover, the small circle is tangent to both other circles, hence we have
axis. Moreover, the small circle is tangent to both other circles, hence we have  and
and  .
.We have
 and
and  . Hence we get the following two equations:
. Hence we get the following two equations:
Simplifying both, we get

As in our case both
 and
and  are positive, we can divide the second one by the first one to get
are positive, we can divide the second one by the first one to get  .
.Now there are two possibilities: either
 , or
, or  . In the first case clearly
. In the first case clearly  , hence this is not the correct case. (Note: This case corresponds to the other circle that is tangent to both given circles and the
, hence this is not the correct case. (Note: This case corresponds to the other circle that is tangent to both given circles and the  axis - a large circle whose center is somewhere to the left of
axis - a large circle whose center is somewhere to the left of  .) The second case solves to
.) The second case solves to  . We then have
. We then have  , hence
, hence  .
.Solution 2
The horizontal line is the equivalent of a circle of curvature
 , thus we can apply Descartes' Circle Formula.
, thus we can apply Descartes' Circle Formula.The four circles have curvatures
 , and
, and  .
.We have

Simplifying, we get

![[frac{1}{r^2}-frac{5}{2r}+frac{9}{16}=0]](https://latex.artofproblemsolving.com/c/9/5/c957bc84cc47e83e5e9884502b84a138490bfc1b.png)
![[frac{16}{r^2}-frac{40}{r}+9=0]](https://latex.artofproblemsolving.com/e/4/d/e4d794221ddb24371d77ede48efe233cb2f2eeb6.png)
![[left(frac{4}{r}-9right)left(frac{4}{r}-1right)=0]](https://latex.artofproblemsolving.com/6/5/b/65bf17396c32cd68738bb5351df8bb5947ff5633.png)
Obviously
 cannot equal
cannot equal  , therefore
, therefore  .
. - We are given
 . So the product of the roots is
. So the product of the roots is  by Vieta's formulas. These also tell us that
by Vieta's formulas. These also tell us that  is the average of the zeros, so
is the average of the zeros, so  . We are also given that the sum of the coefficients is
. We are also given that the sum of the coefficients is  , so
, so  . So the answer is
. So the answer is  .
. ![[asy] pair A=(3,9), B=(1,1), C=(5,3), D=(7,3); draw(A--B--C--D--cycle); label("$A$",A,N); label("$B$",B,SW); label("$C$",C,N); label("$D$",D,E); pair AB = (A + B)/2, BC = (B + C)/2, CD = (C + D)/2, DA = (D + A)/2; draw(AB--BC--CD--DA--cycle); [/asy]](https://latex.artofproblemsolving.com/8/c/f/8cfb9d6da99381de67ea5f718469d0ecfdf8c71c.png) We already know two vertices of the square:
We already know two vertices of the square:  and
and  .There are only two possibilities for the other vertices of the square: either they are
.There are only two possibilities for the other vertices of the square: either they are  and
and  , or they are
, or they are  and
and  . The second case would give us
. The second case would give us  outside the first quadrant, hence the first case is the correct one. As
outside the first quadrant, hence the first case is the correct one. As  is the midpoint of
is the midpoint of  , we can compute
, we can compute  , and
, and  .
.-
Solution 1
Using Simon's Favorite Factoring Trick, we can rewrite the three equations as follows:

Let
 . We get:
. We get:
Clearly
 divides
divides  . On the other hand,
. On the other hand,  can not divide
can not divide  , as it then would divide
, as it then would divide  . Similarly,
. Similarly,  can not divide
can not divide  . Hence
. Hence  divides both
divides both  and
and  . This leaves us with only two cases:
. This leaves us with only two cases:  and
and  .
.The first case solves to
 , which gives us
, which gives us  , but then
, but then  . We do not need to multiply, it is enough to note e.g. that the left hand side is not divisible by
. We do not need to multiply, it is enough to note e.g. that the left hand side is not divisible by  . (Also, a - d equals
. (Also, a - d equals  in this case, which is way too large to fit the answer choices.)
in this case, which is way too large to fit the answer choices.)The second case solves to
 , which gives us a valid quadruple
, which gives us a valid quadruple  , and we have
, and we have  .
. ![[asy] unitsize(0.5cm); defaultpen(0.8); pair A=(0,0), B=(10,0), C=(10,7), D=(0,7), E=(C+D)/2, F=(2*A+B)/3, G=(A+2*B)/3; pair H = intersectionpoint(A--C,E--F); pair J = intersectionpoint(A--C,E--G); draw(A--B--C--D--cycle); draw(G--E--F); draw(A--C); label("$A$",A,SW); label("$B$",B,SE); label("$C$",C,NE); label("$D$",D,NW); label("$E$",E,N); label("$F$",F,S); label("$G$",G,S); label("$H$",H,SE); label("$J$",J,ESE); filldraw(E--H--J--cycle,lightgray,black); draw(H--D, dashed); [/asy]](https://latex.artofproblemsolving.com/9/a/2/9a278ad87dee630d4e8a9f3184f318a012d96823.png)
Solution 1
Note that the triangles
 and
and  are similar, as they have the same angles. Hence
are similar, as they have the same angles. Hence  .
.Also, triangles
 and
and  are similar, hence
are similar, hence  .
.We can now compute
![$[EHJ]$](https://latex.artofproblemsolving.com/5/3/9/539aaebf35d98cd1978db1923158980b14ce837b.png) as
as ![$[ACD]-[AHD]-[DEH]-[EJC]$](https://latex.artofproblemsolving.com/3/3/9/339a4775d05dffa7b5ea0ff2c1a04a3270c735ce.png) . We have:
. We have:![$[ACD]=frac{[ABCD]}2 = 35$](https://latex.artofproblemsolving.com/4/a/b/4ab40167146b47e3148eb7c1ad423c0619c7afbf.png) .
.![$[AHD]$](https://latex.artofproblemsolving.com/a/e/4/ae49b8926c80ae9ff280756155672403d4ee59ed.png) is
is  of
of ![$[ACD]$](https://latex.artofproblemsolving.com/f/a/1/fa16d5df87a703864688635578a8f358b31ad6ef.png) , as these two triangles have the same base
, as these two triangles have the same base  , and
, and  is
is  of
of  , therefore also the height from
, therefore also the height from  onto
onto  is
is  of the height from
of the height from  . Hence
. Hence ![$[AHD]=14$](https://latex.artofproblemsolving.com/a/4/6/a46dfac7ff4cf8f627df7bae2745cdfe652cf6aa.png) .
.![$[HED]$](https://latex.artofproblemsolving.com/9/0/e/90e20418483156d51a828408834897f65f7941ec.png) is
is  of
of ![$[ACD]$](https://latex.artofproblemsolving.com/f/a/1/fa16d5df87a703864688635578a8f358b31ad6ef.png) , as the base
, as the base  is
is  of the base
of the base  , and the height from
, and the height from  is
is  of the height from
of the height from  . Hence
. Hence ![$[HED]=frac {21}2$](https://latex.artofproblemsolving.com/d/3/6/d36d26be959fa5d89a4e76f0bea0b12a59ce57bb.png) .
.![$[JEC]$](https://latex.artofproblemsolving.com/5/a/2/5a28aa4ed0924bf192db9c61376a20342528ba1a.png) is
is  of
of ![$[ACD]$](https://latex.artofproblemsolving.com/f/a/1/fa16d5df87a703864688635578a8f358b31ad6ef.png) for similar reasons, hence
for similar reasons, hence ![$[JEC]=frac{15}2$](https://latex.artofproblemsolving.com/2/f/b/2fbdc39cff57d13f872e4163dea01d2bce3ae3c0.png) .
.
Therefore
![$[EHJ]=[ACD]-[AHD]-[DEH]-[EJC]=35-14-frac {21}2-frac{15}2 = boxed{3}$](https://latex.artofproblemsolving.com/9/1/e/91e2595e101ccfa1a80148e7a583cc27cdf27661.png) .
.Solution 2
As in the previous solution, we note the similar triangles and prove that
 is in
is in  and
and  in
in  of
of  .
.We can then compute that
 .
.As
 is the midpoint of
is the midpoint of  , the height from
, the height from  onto
onto  is
is  of the height from
of the height from  onto
onto  . Therefore we have
. Therefore we have ![$[EHJ] = frac{6}{35} cdot frac 12 cdot [ACD] = frac 3{35} cdot 35 = boxed{3}$](https://latex.artofproblemsolving.com/3/a/3/3a3a60419dfb9be9c6f8561b96eaf4758d1429f2.png) .
.- Let the polynomial be
 and let the two integer zeros be
and let the two integer zeros be  and
and  . We can then write
. We can then write  for some integers
for some integers  and
and  .If a complex number
.If a complex number  with
with  is a root of
is a root of  , it must be the root of
, it must be the root of  , and the other root of
, and the other root of  must be
must be  .We can then write
.We can then write  .We can now examine each of the five given complex numbers, and find the one for which the values
.We can now examine each of the five given complex numbers, and find the one for which the values  and
and  are integers. This is
are integers. This is  , for which we have
, for which we have  and
and  .(As an example, the polynomial
.(As an example, the polynomial  has zeroes
has zeroes  ,
,  , and
, and  .)
.)
Solution 2
By Vieta, we know that the product of all four zeros of the polynomial equals the constant at the end of the polynomial. We also know that the two imaginary roots are a conjugate pair (I.E if one is a+bi, the other is a-bi). So the two imaginary roots must multiply to give you an integer. Taking the 5 answers into hand, we find that
 is our only integer giving solution.
is our only integer giving solution.Solution 3
After dividing the polynomial out by
 and
and  , where p and q are the real roots of the polynomial, we will obtain a quadratic with two complex roots. We can then use the quadratic formula to solve for these complex roots.
, where p and q are the real roots of the polynomial, we will obtain a quadratic with two complex roots. We can then use the quadratic formula to solve for these complex roots.Let's start by using synthetic division to divide
 by
by  . Using this method, the quotient becomes
. Using this method, the quotient becomes  . However, we know that there should be no remainder because
. However, we know that there should be no remainder because  is a factor of the polynomial, so
is a factor of the polynomial, so  must equal 0, so
must equal 0, so  . When we divide the expression on the left by -p, we get
. When we divide the expression on the left by -p, we get  , so we can replace it in our original synthetic division equation with
, so we can replace it in our original synthetic division equation with  .
.We then want to synthetically divide
 by the next factor,
by the next factor,  . Using the same method as before, we can simplify the quotient to
. Using the same method as before, we can simplify the quotient to  . Now for the easy part!
. Now for the easy part!Use the quadratic formula to determine the form of the complex roots.

Now this is starting to look a lot like answers A and E. Noticing that the real part in each answer choice is
 ,
,  and
and  , and the imaginary part is positive. Furthermore, by Vieta's Formulas, we know that d must be a multiple of p and q, so
, and the imaginary part is positive. Furthermore, by Vieta's Formulas, we know that d must be a multiple of p and q, so  is a multiple of 4. Rearranging the expression, we get:
is a multiple of 4. Rearranging the expression, we get:
The radicand therefore must be one less than a multiple of four, which is only the case in
 or
or  .
. -
Solution 1
![[asy] unitsize(2cm); defaultpen(0.8); pair A=(0,0), B=(4,0), D=intersectionpoint( A -- (dir(15)*100), B -- (B+100*dir(135)) ), C=B+3*(D-B); pair ortho=rotate(-90)*(D-A); pair E=extension(C, ortho, A, B); draw(A--B); draw(B--C); draw(A--C); draw(C--E); draw(E--D); draw(A--D); label("$A$",A,SW); label("$B$",B,SE); label("$C$",C,N); label("$D$",D,NE); label("$E$",E,S); [/asy]](https://latex.artofproblemsolving.com/c/f/8/cf87b019e7429c169a048cb720d1c7c31ab79440.png)
We start with the observation that
 , and
, and  .
.We can draw the height
 from
from  onto
onto  . In the triangle
. In the triangle  , we have
, we have  . Hence
. Hence  .
.By the definition of
 , we also have
, we also have  , therefore
, therefore  . This means that the triangle
. This means that the triangle  is isosceles, and as
is isosceles, and as  , we must have
, we must have  .
.Then we compute
 , thus
, thus  and the triangle
and the triangle  is isosceles as well. Hence
is isosceles as well. Hence  .
.Now we can note that
 , hence also the triangle
, hence also the triangle  is isosceles and we have
is isosceles and we have  .
.Combining the previous two observations we get that
 , and as
, and as  , this means that
, this means that  .
.Finally, we get
 .
.Solution 2
Draw a good diagram! Now, let's call
 , so
, so  . Given the rather nice angles of
. Given the rather nice angles of  and
and  as you can see, let's do trig. Drop an altitude from
as you can see, let's do trig. Drop an altitude from  to
to  ; call this point
; call this point  . We realize that there is no specific factor of
. We realize that there is no specific factor of  we can call this just yet, so let
we can call this just yet, so let  . Notice that in
. Notice that in  we get
we get  . Using the 60-degree angle in
. Using the 60-degree angle in  , we obtain
, we obtain  . The comparable ratio is that
. The comparable ratio is that  . If we involve our
. If we involve our  , we get:
, we get: . Eliminating
. Eliminating  and removing radicals from the denominator, we get
and removing radicals from the denominator, we get  . From there, one can easily obtain
. From there, one can easily obtain  . Now we finally have a desired ratio. Since
. Now we finally have a desired ratio. Since  upon calculation, we know that
upon calculation, we know that  can be simplified. Indeed, if you know that
can be simplified. Indeed, if you know that  or even take a minute or two to work out the sine and cosine using
or even take a minute or two to work out the sine and cosine using  , and perhaps the half- or double-angle formulas, you get
, and perhaps the half- or double-angle formulas, you get  .
.Solution 3
Without loss of generality, we can assume that
 and
and  . As above, we are able to find that
. As above, we are able to find that  and
and  .
.Using Law of Sines on triangle
 , we find that
, we find that  . Since we know that
. Since we know that  ,
,  , and
, and  , we can compute
, we can compute  to equal
to equal  and
and  to be
to be  .
.Next, we apply Law of Cosines to triangle
 to see that
to see that  . Simplifying the right side, we get
. Simplifying the right side, we get  , so
, so  .
.Now, we apply Law of Sines to triangle
 to see that
to see that  . After rearranging and noting that
. After rearranging and noting that  , we get
, we get  .
.Dividing the right side by
 , we see that
, we see that  , so
, so  is either
is either  or
or  . Since
. Since  is not a choice, we know
is not a choice, we know  .
.Note that we can also confirm that
 by computing
by computing  with Law of Sines.
with Law of Sines. - It never hurts to compute a few terms of the sequence in order to get a feel how it looks like. In our case, the definition is that
 . This can be rewritten as
. This can be rewritten as  . We have
. We have  and
and  , and we compute:
, and we compute: At this point we see that the sequence will become periodic: we have
At this point we see that the sequence will become periodic: we have  ,
,  , and each subsequent term is uniquely determined by the previous two.Hence if
, and each subsequent term is uniquely determined by the previous two.Hence if  appears, it has to be one of
appears, it has to be one of  to
to  . As
. As  , we only have four possibilities left. Clearly
, we only have four possibilities left. Clearly  for
for  , and
, and  for
for  . The equation
. The equation  solves to
solves to  , and the equation
, and the equation  to
to  .No two values of
.No two values of  we just computed are equal, and therefore there are
we just computed are equal, and therefore there are  different values of
different values of  for which the sequence contains the value
for which the sequence contains the value 
以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









