- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2000 AMC12真题及答案详细解析
2000 AMC 12 真题
答案详细解析请参考文末
Problem 1
In the year ![]() , the United States will host the International Mathematical Olympiad. Let
, the United States will host the International Mathematical Olympiad. Let ![]() and
and ![]() be distinct positive integers such that the product
be distinct positive integers such that the product ![]() . What is the largest possible value of the sum
. What is the largest possible value of the sum ![]() ?
? ![]()
Problem 2
![]()
![]()
Problem 3
Each day, Jenny ate ![]() of the jellybeans that were in her jar at the beginning of that day. At the end of the second day,
of the jellybeans that were in her jar at the beginning of that day. At the end of the second day, ![]() remained. How many jellybeans were in the jar originally?
remained. How many jellybeans were in the jar originally? ![]()
Problem 4
The Fibonacci sequence ![]() starts with two
starts with two ![]() 's, and each term afterwards is the sum of its two predecessors. Which one of the ten digits is the last to appear in the units position of a number in the Fibonacci sequence?
's, and each term afterwards is the sum of its two predecessors. Which one of the ten digits is the last to appear in the units position of a number in the Fibonacci sequence? ![]()
Problem 5
If ![]() where
where ![]() then
then ![]()
![]()
Problem 6
Two different prime numbers between ![]() and
and ![]() are chosen. When their sum is subtracted from their product, which of the following numbers could be obtained?
are chosen. When their sum is subtracted from their product, which of the following numbers could be obtained? ![]()
Problem 7
How many positive integers ![]() have the property that
have the property that ![]() is a positive integer?
is a positive integer? ![]()
Problem 8
Figures ![]() ,
, ![]() ,
, ![]() , and
, and ![]() consist of
consist of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() nonoverlapping unit squares, respectively. If the pattern were continued, how many nonoverlapping unit squares would there be in figure 100?
nonoverlapping unit squares, respectively. If the pattern were continued, how many nonoverlapping unit squares would there be in figure 100? ![[asy] unitsize(8); draw((0,0)--(1,0)--(1,1)--(0,1)--cycle); draw((9,0)--(10,0)--(10,3)--(9,3)--cycle); draw((8,1)--(11,1)--(11,2)--(8,2)--cycle); draw((19,0)--(20,0)--(20,5)--(19,5)--cycle); draw((18,1)--(21,1)--(21,4)--(18,4)--cycle); draw((17,2)--(22,2)--(22,3)--(17,3)--cycle); draw((32,0)--(33,0)--(33,7)--(32,7)--cycle); draw((29,3)--(36,3)--(36,4)--(29,4)--cycle); draw((31,1)--(34,1)--(34,6)--(31,6)--cycle); draw((30,2)--(35,2)--(35,5)--(30,5)--cycle); label("Figure",(0.5,-1),S); label("$0$",(0.5,-2.5),S); label("Figure",(9.5,-1),S); label("$1$",(9.5,-2.5),S); label("Figure",(19.5,-1),S); label("$2$",(19.5,-2.5),S); label("Figure",(32.5,-1),S); label("$3$",(32.5,-2.5),S); [/asy]](https://latex.artofproblemsolving.com/a/3/0/a3059e62f90ea366f648ad6fc7511221a4977855.png)
![]()
Problem 9
Mrs. Walter gave an exam in a mathematics class of five students. She entered the scores in random order into a spreadsheet, which recalculated the class average after each score was entered. Mrs. Walter noticed that after each score was entered, the average was always an integer. The scores (listed in ascending order) were ![]() and
and ![]() . What was the last score Mrs. Walters entered?
. What was the last score Mrs. Walters entered? ![]()
Problem 10
The point ![]() is reflected in the
is reflected in the ![]() -plane, then its image
-plane, then its image ![]() is rotated
is rotated ![]() about the
about the ![]() -axis to produce
-axis to produce ![]() , and finally,
, and finally, ![]() is translated
is translated![]() units in the positive-
units in the positive-![]() direction to produce
direction to produce ![]() . What are the coordinates of
. What are the coordinates of ![]() ?
? ![]()
Problem 11
Two non-zero real numbers, ![]() and
and ![]() satisfy
satisfy ![]() . Which of the following is a possible value of
. Which of the following is a possible value of ![]() ?
? ![]()
Problem 12
Let ![]() and
and ![]() be nonnegative integers such that
be nonnegative integers such that ![]() . What is the maximum value of
. What is the maximum value of ![]() ?
? ![]()
Problem 13
One morning each member of Angela’s family drank an ![]() -ounce mixture of coffee with milk. The amounts of coffee and milk varied from cup to cup, but were never zero. Angela drank a quarter of the total amount of milk and a sixth of the total amount of coffee. How many people are in the family?
-ounce mixture of coffee with milk. The amounts of coffee and milk varied from cup to cup, but were never zero. Angela drank a quarter of the total amount of milk and a sixth of the total amount of coffee. How many people are in the family? ![]()
Problem 14
When the mean, median, and mode of the list ![]() are arranged in increasing order, they form a non-constant arithmetic progression. What is the sum of all possible real values of
are arranged in increasing order, they form a non-constant arithmetic progression. What is the sum of all possible real values of ![]() ?
? ![]()
Problem 15
Let ![]() be a function for which
be a function for which ![]() . Find the sum of all values of
. Find the sum of all values of ![]() for which
for which ![]() .
. ![]()
Problem 16
A checkerboard of ![]() rows and
rows and ![]() columns has a number written in each square, beginning in the upper left corner, so that the first row is numbered
columns has a number written in each square, beginning in the upper left corner, so that the first row is numbered ![]() , the second row
, the second row ![]() , and so on down the board. If the board is renumbered so that the left column, top to bottom, is
, and so on down the board. If the board is renumbered so that the left column, top to bottom, is ![]() , the second column
, the second column ![]() and so on across the board, some squares have the same numbers in both numbering systems. Find the sum of the numbers in these squares (under either system).
and so on across the board, some squares have the same numbers in both numbering systems. Find the sum of the numbers in these squares (under either system). ![]()
Problem 17
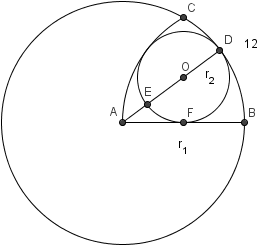
A circle centered at ![]() has radius
has radius ![]() and contains the point
and contains the point ![]() . The segment
. The segment ![]() is tangent to the circle at
is tangent to the circle at ![]() and
and ![]() . If point
. If point ![]() lies on
lies on ![]() and
and ![]() bisects
bisects ![]() , then
, then ![]()
![]()
Problem 18
In year ![]() , the
, the ![]() th day of the year is a Tuesday. In year
th day of the year is a Tuesday. In year ![]() , the
, the ![]() th day is also a Tuesday. On what day of the week did the
th day is also a Tuesday. On what day of the week did the ![]() th day of year
th day of year ![]() occur?
occur? ![]()
Problem 19
In triangle ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Let
. Let ![]() denote the midpoint of
denote the midpoint of ![]() and let
and let ![]() denote the intersection of
denote the intersection of ![]() with the bisector of angle
with the bisector of angle ![]() . Which of the following is closest to the area of the triangle
. Which of the following is closest to the area of the triangle ![]() ?
? ![]()
Problem 20
If ![]() and
and ![]() are positive numbers satisfying
are positive numbers satisfying ![]() and
and ![]() then what is the value of
then what is the value of ![]() ?
? ![]()
Problem 21
Through a point on the hypotenuse of a right triangle, lines are drawn parallel to the legs of the triangle so that the triangle is divided into a square and two smaller right triangles. The area of one of the two small right triangles is ![]() times the area of the square. The ratio of the area of the other small right triangle to the area of the square is
times the area of the square. The ratio of the area of the other small right triangle to the area of the square is ![]()
Problem 22
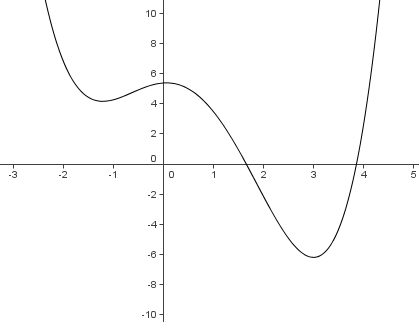
The graph below shows a portion of the curve defined by the quartic polynomial ![]() . Which of the following is the smallest?
. Which of the following is the smallest? 
Problem 23
Professor Gamble buys a lottery ticket, which requires that he pick six different integers from ![]() through
through ![]() , inclusive. He chooses his numbers so that the sum of the base-ten logarithms of his six numbers is an integer. It so happens that the integers on the winning ticket have the same property— the sum of the base-ten logarithms is an integer. What is the probability that Professor Gamble holds the winning ticket?
, inclusive. He chooses his numbers so that the sum of the base-ten logarithms of his six numbers is an integer. It so happens that the integers on the winning ticket have the same property— the sum of the base-ten logarithms is an integer. What is the probability that Professor Gamble holds the winning ticket? ![]()
Problem 24
If circular arcs ![]() and
and ![]() have centers at
have centers at ![]() and
and ![]() , respectively, then there exists a circle tangent to both
, respectively, then there exists a circle tangent to both ![]() and
and ![]() , and to
, and to ![]() . If the length of
. If the length of ![]() is
is ![]() , then the circumference of the circle is
, then the circumference of the circle is ![]()
Problem 25
Eight congruent equilateral triangles, each of a different color, are used to construct a regular octahedron. How many distinguishable ways are there to construct the octahedron? (Two colored octahedrons are distinguishable if neither can be rotated to look just like the other.) ![]()
![[asy] import three; import math; unitsize(1.5cm); currentprojection=orthographic(2,0.2,1); triple A=(0,0,1); triple B=(sqrt(2)/2,sqrt(2)/2,0); triple C=(sqrt(2)/2,-sqrt(2)/2,0); triple D=(-sqrt(2)/2,-sqrt(2)/2,0); triple E=(-sqrt(2)/2,sqrt(2)/2,0); triple F=(0,0,-1); draw(A--B--E--cycle); draw(A--C--D--cycle); draw(F--C--B--cycle); draw(F--D--E--cycle,dotted+linewidth(0.7)); [/asy]](https://latex.artofproblemsolving.com/7/d/1/7d13f21ea69c61ec44e671434db41a0bdedb8189.png)
2000 AMC12 真题答案详细解析
- 1.The sum is the highest if two factors are the lowest.
So, and
and  .
. 
- Since Jenny eats
 of her jelly beans per day,
of her jelly beans per day,  of her jelly beans remain after one day.Let
of her jelly beans remain after one day.Let  be the number of jelly beans in the jar originally.
be the number of jelly beans in the jar originally.


- Note that any digits other than the units digit will not affect the answer. So to make computation quicker, we can just look at the Fibonacci sequence in
 :
: The last digit to appear in the units position of a number in the Fibonacci sequence is
The last digit to appear in the units position of a number in the Fibonacci sequence is  .
. - When

 is negative so
is negative so  and
and  .Thus
.Thus  .
. 
-
Solution 1
All prime numbers between 4 and 18 have an odd product and an even sum. Any odd number minus an even number is an odd number, so we can eliminate B, D, and A. Since the highest two prime numbers we can pick are 13 and 17, the highest number we can make is
 . Thus, we can eliminate E. So, the answer must be
. Thus, we can eliminate E. So, the answer must be  .
.Solution 2
Let the two primes be
 and
and  . We wish to obtain the value of
. We wish to obtain the value of  , or
, or  . Using Simon's Favorite Factoring Trick, we can rewrite this expression as
. Using Simon's Favorite Factoring Trick, we can rewrite this expression as  or
or  . Noticing that
. Noticing that  , we see that the answer is
, we see that the answer is  .
.Solution 3
The answer must be in the form
 =
=  . Since
. Since  and
and  are both even,
are both even,  is
is  , and the only answer that is
, and the only answer that is  is
is  .
. - If
 , then
, then  . Since
. Since  ,
,  must be
must be  to some factor of 6. Thus, there are four (3, 9, 27, 729) possible values of
to some factor of 6. Thus, there are four (3, 9, 27, 729) possible values of 
 .
. - Figures
 ,
,  ,
,  , and
, and  consist of
consist of  ,
,  ,
,  , and
, and  nonoverlapping unit squares, respectively. If the pattern were continued, how many nonoverlapping unit squares would there be in figure 100?
nonoverlapping unit squares, respectively. If the pattern were continued, how many nonoverlapping unit squares would there be in figure 100?![[asy] unitsize(8); draw((0,0)--(1,0)--(1,1)--(0,1)--cycle); draw((9,0)--(10,0)--(10,3)--(9,3)--cycle); draw((8,1)--(11,1)--(11,2)--(8,2)--cycle); draw((19,0)--(20,0)--(20,5)--(19,5)--cycle); draw((18,1)--(21,1)--(21,4)--(18,4)--cycle); draw((17,2)--(22,2)--(22,3)--(17,3)--cycle); draw((32,0)--(33,0)--(33,7)--(32,7)--cycle); draw((29,3)--(36,3)--(36,4)--(29,4)--cycle); draw((31,1)--(34,1)--(34,6)--(31,6)--cycle); draw((30,2)--(35,2)--(35,5)--(30,5)--cycle); label("Figure",(0.5,-1),S); label("$0$",(0.5,-2.5),S); label("Figure",(9.5,-1),S); label("$1$",(9.5,-2.5),S); label("Figure",(19.5,-1),S); label("$2$",(19.5,-2.5),S); label("Figure",(32.5,-1),S); label("$3$",(32.5,-2.5),S); [/asy]](https://latex.artofproblemsolving.com/a/3/0/a3059e62f90ea366f648ad6fc7511221a4977855.png)

Solution 1
We can divide up figure
 to get the sum of the sum of the first
to get the sum of the sum of the first  odd numbers and the sum of the first
odd numbers and the sum of the first  odd numbers. If you do not see this, here is the example for
odd numbers. If you do not see this, here is the example for  :
: ![[asy] draw((3,0)--(4,0)--(4,7)--(3,7)--cycle); draw((0,3)--(7,3)--(7,4)--(0,4)--cycle); draw((2,1)--(5,1)--(5,6)--(2,6)--cycle); draw((1,2)--(6,2)--(6,5)--(1,5)--cycle); draw((3,0)--(3,7)); [/asy]](https://latex.artofproblemsolving.com/4/c/a/4ca4b0deb1105c8c96fa81ac967fa015585e8a09.png) The sum of the first
The sum of the first  odd numbers is
odd numbers is  , so for figure
, so for figure  , there are
, there are  unit squares. We plug in
unit squares. We plug in  to get
to get  .
.Solution 2
Using the recursion from solution 1, we see that the first differences of
 form an arithmetic progression, and consequently that the second differences are constant and all equal to
form an arithmetic progression, and consequently that the second differences are constant and all equal to  . Thus, the original sequence can be generated from a quadratic function.
. Thus, the original sequence can be generated from a quadratic function.
If , and
, and  ,
,  , and
, and  , we get a system of three equations in three variables:
, we get a system of three equations in three variables:  gives
gives 
 gives
gives 
 gives
gives  Plugging in
Plugging in  into the last two equations gives
into the last two equations gives 
 Dividing the second equation by 2 gives the system:
Dividing the second equation by 2 gives the system: 
 Subtracting the first equation from the second gives
Subtracting the first equation from the second gives  , and hence
, and hence  . Thus, our quadratic function is:
. Thus, our quadratic function is:  Calculating the answer to our problem,
Calculating the answer to our problem,  , which is choice
, which is choice  .
.Solution 3
We can see that each figure
 has a central box and 4 columns of
has a central box and 4 columns of  boxes on each side of each square. Therefore, at figure 100, there is a central box with 100 boxes on the top, right, left, and bottom. Knowing that each quarter of each figure has a pyramid structure, we know that for each quarter there are
boxes on each side of each square. Therefore, at figure 100, there is a central box with 100 boxes on the top, right, left, and bottom. Knowing that each quarter of each figure has a pyramid structure, we know that for each quarter there are  squares.
squares.  . Adding in the original center box we have
. Adding in the original center box we have  .
.Solution 4
Let
 be the number of squares in figure
be the number of squares in figure  . We can easily see that
. We can easily see that![[a_0=4cdot 0+1]](https://latex.artofproblemsolving.com/5/d/c/5dc9a74825f56cc67818fcb8da61611aa619e414.png)
![[a_1=4cdot 1+1]](https://latex.artofproblemsolving.com/4/2/3/42333188c291802f779e9ada597c0c1ecd0f7612.png)
![[a_2=4cdot 3+1]](https://latex.artofproblemsolving.com/1/7/e/17e5662f437a0dd809f4c98d4af2fda33df460a4.png)
![[a_3=4cdot 6+1.]](https://latex.artofproblemsolving.com/4/0/9/40989a0be2f62369eb9f61dc773f48cee14772fa.png) Note that in
Note that in  , the number multiplied by the 4 is the
, the number multiplied by the 4 is the  th triangular number. Hence,
th triangular number. Hence,  .
.Solution 5
Let
 denote the number of unit cubes in a figure. We have
denote the number of unit cubes in a figure. We have![[f_0=1]](https://latex.artofproblemsolving.com/a/6/8/a68548667e85fb7a1ceb529aeb3975604cbd3e7e.png)
![[f_1=5]](https://latex.artofproblemsolving.com/d/f/9/df9da1dce71b4af5aa60ab84bd8ae2b8ed11a38d.png)
![[f_2=13]](https://latex.artofproblemsolving.com/7/7/e/77e6d1a8da60db4cac72066a0c7a0c30ddc9b778.png)
![[f_3=25]](https://latex.artofproblemsolving.com/a/7/a/a7ad38505436381fe9a4cdf07181bf8441742b3a.png)
![[f_4=41]](https://latex.artofproblemsolving.com/8/c/d/8cd035244016a30d66fc6fb7b3a369de529b337a.png)
![[...]](https://latex.artofproblemsolving.com/a/7/7/a77a80061f2acc5bff28985d471dadc862f24425.png) Computing the difference between the number of cubes in each figure yields
Computing the difference between the number of cubes in each figure yields![[4,8,12,16,...]](https://latex.artofproblemsolving.com/2/3/2/232c75d3df10e5c1d636b116ab65f6f20e914ece.png) It is easy to notice that this is an arithmetic sequence, with the first term being
It is easy to notice that this is an arithmetic sequence, with the first term being  and the difference being
and the difference being  . Let this sequence be
. Let this sequence be  From
From  to
to  , the sequence will have
, the sequence will have  terms. Using the arithmetic sum formula yields
terms. Using the arithmetic sum formula yields ![[S_{100}=frac{100[2cdot 4+(100-1)4]}{2}]](https://latex.artofproblemsolving.com/8/1/b/81b7a889e6da0f89d4ecdfb661bca09a9153c685.png)
![[=50(2cdot 4+99cdot 4)]](https://latex.artofproblemsolving.com/7/e/6/7e61189e062c7042382a690103c492e3ab31aa7c.png)
![[=50(101cdot 4)]](https://latex.artofproblemsolving.com/3/5/4/354d5197b9067499660dc344446baf87bc8fe7bc.png)
![[=200cdot 101]](https://latex.artofproblemsolving.com/0/6/b/06be38292ce7677b10f31101d9faba281ec327a6.png)
![[=20200]](https://latex.artofproblemsolving.com/3/2/8/328f29ab41ca9bd4a339aa2c91ae975d20f84dd5.png) So
So  unit cubes.
unit cubes. -
Solution 1
The first number is divisible by 1.
The sum of the first two numbers is even.
The sum of the first three numbers is divisible by 3.
The sum of the first four numbers is divisible by 4.
The sum of the first five numbers is 400.
Since 400 is divisible by 4, the last score must also be divisible by 4. Therefore, the last score is either 76 or 80.
Case 1: 76 is the last number entered.
Since , the fourth number must be divisible by 3, but none of the scores are divisible by 3.
, the fourth number must be divisible by 3, but none of the scores are divisible by 3.
Case 2: 80 is the last number entered.
Since , the fourth number must be
, the fourth number must be  . That number is 71 and 71 only. The next number must be 91, since the sum of the first two numbers is even. So the only arrangement of the scores
. That number is 71 and 71 only. The next number must be 91, since the sum of the first two numbers is even. So the only arrangement of the scores 

Solution 2
We know the first sum of the first three numbers must be divisible by 3, so we write out all 5 numbers
 , which gives 2,1,2,1,1, respectively. Clearly, the only way to get a number divisible by 3 by adding three of these is by adding the three ones. So those must go first. Now we have an odd sum, and since the next average must be divisible by 4, 71 must be next. That leaves 80 for last, so the answer is
, which gives 2,1,2,1,1, respectively. Clearly, the only way to get a number divisible by 3 by adding three of these is by adding the three ones. So those must go first. Now we have an odd sum, and since the next average must be divisible by 4, 71 must be next. That leaves 80 for last, so the answer is  .
. - Step 1: Reflect in the xy plane. Replace z with its additive inverse:
 Step 2: Rotate around x-axis 180 degrees. Replace y and z with their respective additive inverses.
Step 2: Rotate around x-axis 180 degrees. Replace y and z with their respective additive inverses.  Step 3: Translate 5 units in positive-y direction. Replace y with y+5.
Step 3: Translate 5 units in positive-y direction. Replace y with y+5. 
 .Another way is to solve the equation for
.Another way is to solve the equation for  giving
giving  then substituting this into the expression and simplifying gives the answer of
then substituting this into the expression and simplifying gives the answer of 
Solution 2
This simplifies to
 . The two integer solutions to this are
. The two integer solutions to this are  and
and  . The problem states than
. The problem states than  and
and  are non-zero, so we consider the case of
are non-zero, so we consider the case of  . So, we end up with
. So, we end up with 
-
Solution 1
It is not hard to see that
![[(A+1)(M+1)(C+1)=]](https://latex.artofproblemsolving.com/e/1/a/e1a20a664fc92825a76c41415d24fe902a9e4fb1.png)
![[AMC+AM+AC+MC+A+M+C+1]](https://latex.artofproblemsolving.com/7/b/6/7b615f683ed979dc734b1fc7c95d4b8765e5d094.png) Since
Since  , we can rewrite this as
, we can rewrite this as![[(A+1)(M+1)(C+1)=]](https://latex.artofproblemsolving.com/e/1/a/e1a20a664fc92825a76c41415d24fe902a9e4fb1.png)
![[AMC+AM+AC+MC+13]](https://latex.artofproblemsolving.com/7/9/f/79f3f8b8cb3dee37405c83c414548b1ebd2a63c5.png) So we wish to maximize
So we wish to maximize![[(A+1)(M+1)(C+1)-13]](https://latex.artofproblemsolving.com/a/3/f/a3f9f9ef8289341a9a4f3e43f0aa4199a2d28b58.png) Which is largest when all the factors are equal (consequence of AM-GM). Since
Which is largest when all the factors are equal (consequence of AM-GM). Since  , we set
, we set  Which gives us
Which gives us![[(4+1)(4+1)(4+1)-13=112]](https://latex.artofproblemsolving.com/8/c/c/8cc110b16d54e7fd301a03ee24ee13a2f40e0e05.png) so the answer is
so the answer is  .
.Solution 2
If you know that to maximize your result you have to make the numbers as close together as possible, (for example to maximize area for a polygon make it a square) then you can try to make
 and
and  as close as possible. In this case, they would all be equal to
as close as possible. In this case, they would all be equal to  , so
, so  , giving you the answer of
, giving you the answer of  .
. -
Solution 1
Let
 be the total amount of coffee,
be the total amount of coffee,  of milk, and
of milk, and  the number of people in the family. Then each person drinks the same total amount of coffee and milk (8 ounces), so
the number of people in the family. Then each person drinks the same total amount of coffee and milk (8 ounces), so![[left(frac{c}{6} + frac{m}{4}right)p = c + m]](https://latex.artofproblemsolving.com/a/0/1/a018ae1614ac885a782067b85a8b65ff51f73dca.png) Regrouping, we get
Regrouping, we get  . Since both
. Since both  are positive, it follows that
are positive, it follows that  and
and  are also positive, which is only possible when
are also positive, which is only possible when  .
.Solution 2 (less rigorous)
One could notice that (since there are only two components to the mixture) Angela must have more than her "fair share" of milk and less then her "fair share" of coffee in order to ensure that everyone has
 ounces. The "fair share" is
ounces. The "fair share" is  So,
So, ![[frac{1}{6} < frac{1}{p}<frac{1}{4}]](https://latex.artofproblemsolving.com/e/4/1/e415a2efc92b64fac3e3726552212381b837a91d.png) Which requires that
Which requires that  be
be  since
since  is a whole number.
is a whole number.- The mean is
 .
. - Arranged in increasing order, the list is
 , so the median is either
, so the median is either  or
or  depending upon the value of
depending upon the value of  .
. - The mode is
 , since it appears three times.
, since it appears three times.
- The mean is
-
Solution 1
Let
 ; then
; then  . Thus
. Thus  , and
, and  . These sum up to
. These sum up to 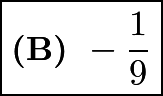 . (We can also use Vieta's formulas to find the sum more quickly.)
. (We can also use Vieta's formulas to find the sum more quickly.)Solution 2
Set
 to get
to get  From either finding the roots or using Vieta's formulas, we find the sum of these roots to be
From either finding the roots or using Vieta's formulas, we find the sum of these roots to be  Each root of this equation is
Each root of this equation is  times greater than a corresponding root of
times greater than a corresponding root of  (because
(because  gives
gives  ), thus the sum of the roots in the equation
), thus the sum of the roots in the equation  is
is  or
or 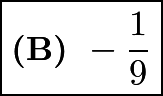 .
.Solution 3
Since we have
 ,
,  occurs at
occurs at  Thus,
Thus,  . We set this equal to 7:
. We set this equal to 7:  . For any quadratic
. For any quadratic  , the sum of the roots is
, the sum of the roots is  . Thus, the sum of the roots of this equation is
. Thus, the sum of the roots of this equation is  .
. - Index the rows with
 Index the columns with
Index the columns with  For the first row number the cells
For the first row number the cells  For the second,
For the second,  and so onSo the number in row =
and so onSo the number in row =  and column =
and column =  is
is  Similarly, numbering the same cells column wise we find the number in row =
Similarly, numbering the same cells column wise we find the number in row =  and column =
and column =  is
is  So we need to solve
So we need to solve



 We get
We get 






-
Solution 1
Since
 is tangent to the circle,
is tangent to the circle,  is a right triangle. This means that
is a right triangle. This means that  ,
,  and
and  . By the Angle Bisector Theorem,
. By the Angle Bisector Theorem,![[frac{OB}{OC} = frac{AB}{AC} Longrightarrow AC sec theta = OC tan theta]](https://latex.artofproblemsolving.com/6/9/7/69707027aaee20cd1affa3ab24e9df267be4e644.png) We multiply both sides by
We multiply both sides by  to simplify the trigonometric functions,
to simplify the trigonometric functions,![[AC=OC sin theta]](https://latex.artofproblemsolving.com/f/e/a/feaa39c521fa4656bbfb421c013a3eb7498dfb68.png) Since
Since  ,
, 
 . Therefore, the answer is
. Therefore, the answer is  .
.Solution 2
Alternatively, one could notice that OC approaches the value 1/2 as theta gets close to 90 degrees. The only choice that is consistent with this is (D).
Solution 3 (with minimal trig)
Let's assign a value to
 so we don't have to use trig functions to solve.
so we don't have to use trig functions to solve.  is a good value for
is a good value for  , because then we have a
, because then we have a  --
--  because
because  is tangent to Circle
is tangent to Circle  .
.
Using our special right triangle, since ,
,  , and
, and  .
.
Let . Then
. Then  . since
. since  bisects
bisects  , we can use the angle bisector theorem:
, we can use the angle bisector theorem: 


 .
.
Now, we only have to use a bit of trig to guess and check: the only trig facts we need to know to finish the problem is:

 .
.
With a bit of guess and check, we get that the answer is .
. - There are either
![[65 + 200 = 265]](https://latex.artofproblemsolving.com/6/2/9/62997404eccda827729e180344fb549322e5596b.png) or
or![[66 + 200 = 266]](https://latex.artofproblemsolving.com/4/1/0/410b22f951be4fd0f5d55cc96280621336ed4ed4.png) days between the first two dates depending upon whether or not year
days between the first two dates depending upon whether or not year  is a leap year. Since
is a leap year. Since  divides into
divides into  but not
but not  , for both days to be a Tuesday, year
, for both days to be a Tuesday, year  must be a leap year.Hence, year
must be a leap year.Hence, year  is not a leap year, and so since there are
is not a leap year, and so since there are![[265 + 300 = 565]](https://latex.artofproblemsolving.com/9/b/b/9bb28446bd7a88948b838d007a8a00e9e3f96965.png) days between the date in years
days between the date in years  , this leaves a remainder of
, this leaves a remainder of  upon division by
upon division by  . Since we are subtracting days, we count 5 days before Tuesday, which gives us
. Since we are subtracting days, we count 5 days before Tuesday, which gives us 
-
Solution 1
The answer is exactly
 , choice
, choice  . We can find the area of triangle
. We can find the area of triangle  by using the simple formula
by using the simple formula  . Dropping an altitude from
. Dropping an altitude from  , we see that it has length
, we see that it has length  ( we can split the large triangle into a
( we can split the large triangle into a  and a
and a  triangle). Then we can apply the Angle Bisector Theorem on triangle
triangle). Then we can apply the Angle Bisector Theorem on triangle  to solve for
to solve for  . Solving
. Solving  , we get that
, we get that  .
.  is the midpoint of
is the midpoint of  so
so  . Thus we get the base of triangle
. Thus we get the base of triangle  , to be
, to be  units long. Applying the formula
units long. Applying the formula  , we get
, we get  .
.Solution 2
The area of
 is
is ![$frac{DEcdot h}{2}=frac{DE}{BC} cdot frac{BCcdot h}{2}=frac{DE}{BC}[ABC]$](https://latex.artofproblemsolving.com/5/f/9/5f94984769a4c9bb96e0c5633395b708e0a4f4ac.png) where
where  is the height of triangle
is the height of triangle  . Using Angle Bisector Theorem, we find
. Using Angle Bisector Theorem, we find  , which we solve to get
, which we solve to get  .
.  is the midpoint of
is the midpoint of  so
so  . Thus we get the base of triangle
. Thus we get the base of triangle  , to be
, to be  units long. We can now use Heron's Formula on
units long. We can now use Heron's Formula on  .
.![[s=frac{AB+BC+AC}{2}=21]](https://latex.artofproblemsolving.com/8/c/5/8c5b5b1ea02313f8c6770b658ef7f00d750d67f7.png)
![[[ABC]=sqrt{(s)(s-AB)(s-BC)(s-AC)}=sqrt{(21)(8)(7)(6)}=84]](https://latex.artofproblemsolving.com/d/7/0/d70c2a368692f018e7970db3d0b67d8ef77e6553.png)
![[frac{DE}{BC}[ABC]=frac{frac{1}{2}}{14}cdot 84=3]](https://latex.artofproblemsolving.com/0/b/0/0b078aa58ff86ab4285096bbbf51e594021c9e29.png) Therefore, the answer is
Therefore, the answer is  .
. -
Solution 1
We multiply all given expressions to get:
![[(1)xyz + x + y + z + frac{1}{x} + frac{1}{y} + frac{1}{z} + frac{1}{xyz} = frac{28}{3}]](https://latex.artofproblemsolving.com/3/9/9/39946093baf76ac36c45716580f910fe4040b79a.png) Adding all the given expressions gives that
Adding all the given expressions gives that![[(2) x + y + z + frac{1}{x} + frac{1}{y} + frac{1}{z} = 4 + frac{7}{3} + 1 = frac{22}{3}]](https://latex.artofproblemsolving.com/b/8/b/b8b3ee76ca8fe7a060cceabcc53fac838de13cc6.png) We subtract
We subtract  from
from  to get that
to get that  . Hence, by inspection,
. Hence, by inspection,  .
.![[]](https://latex.artofproblemsolving.com/5/7/f/57f1406b65f9f2e6a365b7356da731780b42cceb.png) ~AopsUser101
~AopsUser101Solution 2
We have a system of three equations and three variables, so we can apply repeated substitution.
![[4 = x + frac{1}{y} = x + frac{1}{1 - frac{1}{z}} = x + frac{1}{1-frac{1}{7/3-1/x}} = x + frac{7x-3}{4x-3}]](https://latex.artofproblemsolving.com/9/f/0/9f0d43b0925f112e173739d093abd90c9a6ecf41.png) Multiplying out the denominator and simplification yields
Multiplying out the denominator and simplification yields  , so
, so  . Substituting leads to
. Substituting leads to  , and the product of these three variables is
, and the product of these three variables is  .
. -
Solution 1
![[asy] unitsize(36); draw((0,0)--(6,0)--(0,3)--cycle); draw((0,0)--(2,0)--(2,2)--(0,2)--cycle); label("$1$",(1,2),S); label("$1$",(2,1),W); label("$2m$",(4,0),S); label("$x$",(0,2.5),W); [/asy]](https://latex.artofproblemsolving.com/a/f/e/afe29f5d468b8c91dd67e38cbbc66bd25501eaf9.png) WLOG, let a side of the square be
WLOG, let a side of the square be  . Simple angle chasing shows that the two right triangles are similar. Thus the ratio of the sides of the triangles are the same. Since
. Simple angle chasing shows that the two right triangles are similar. Thus the ratio of the sides of the triangles are the same. Since  , the height of the triangle with area
, the height of the triangle with area  is
is  . Therefore
. Therefore  where
where  is the base of the other triangle.
is the base of the other triangle.  , and the area of that triangle is
, and the area of that triangle is  .
.Solution 2
![[asy] unitsize(36); draw((0,0)--(6,0)--(0,3)--cycle); draw((0,0)--(2,0)--(2,2)--(0,2)--cycle); label("$b$",(2.5,0),S); label("$a$",(0,1.5),W); label("$c$",(2.5,1),W); label("$A$",(0.5,2.5),W); label("$B$",(3.5,0.75),W); label("$C$",(1,1),W); [/asy]](https://latex.artofproblemsolving.com/1/f/d/1fd5c48ee1cfa3bcf3bd117fe4798e0440cbb6c5.png) From the diagram from the previous solution, we have
From the diagram from the previous solution, we have  ,
,  as the legs and
as the legs and  as the side length of the square. WLOG, let the area of triangle
as the side length of the square. WLOG, let the area of triangle  be
be  times the area of square
times the area of square  .
.
Since triangle is similar to the large triangle, it has
is similar to the large triangle, it has  ,
,  and
and![[[A] = frac{bh}{2} = frac{ac^2}{2b} = m[C] = mc^2]](https://latex.artofproblemsolving.com/5/c/a/5caa9226761852a91d79f81f0de0ea044cd7f2ee.png) Thus
Thus  Now since triangle
Now since triangle  is similar to the large triangle, it has
is similar to the large triangle, it has  ,
,  and
and![[[B] = frac{bh}{2} = frac{bc^2}{2a} = nc^2 = n[C]]](https://latex.artofproblemsolving.com/c/6/b/c6b5a58f0fd075d73ce1504285a534f546542588.png) Thus
Thus  .
.  .
. - Note that there are 3 maxima/minima. Hence we know that the rest of the graph is greater than 10. We approximate each of the above expressions:
- According to the graph,

- The product of the roots is
 by Vieta’s formulas. Also,
by Vieta’s formulas. Also,  according to the graph.
according to the graph. - The product of the real roots is
 , and the total product is
, and the total product is  (from above), so the product of the non-real roots is
(from above), so the product of the non-real roots is  .
. - The sum of the coefficients is

- The sum of the real roots is
 .
.
Clearly
 is the smallest.
is the smallest. - According to the graph,
- The product of the numbers have to be a power of
 in order to have an integer base ten logarithm. Thus all of the numbers must be in the form
in order to have an integer base ten logarithm. Thus all of the numbers must be in the form  . Listing out such numbers from
. Listing out such numbers from  to
to  , we find
, we find  are the only such numbers. Immediately it should be noticed that there are a larger number of powers of
are the only such numbers. Immediately it should be noticed that there are a larger number of powers of  than of
than of  . Since a number in the form of
. Since a number in the form of  must have the same number of
must have the same number of  s and
s and  s in its factorization, we require larger powers of
s in its factorization, we require larger powers of  than we do of
than we do of  . To see this, for each number subtract the power of
. To see this, for each number subtract the power of  from the power of
from the power of  . This yields
. This yields  , and indeed the only non-positive terms are
, and indeed the only non-positive terms are  . Since there are only two zeros, the largest number that Professor Gamble could have picked would be
. Since there are only two zeros, the largest number that Professor Gamble could have picked would be  .Thus Gamble picks numbers which fit
.Thus Gamble picks numbers which fit  , with the first four having already been determined to be
, with the first four having already been determined to be  . The choices for the
. The choices for the  include
include  and the choices for the
and the choices for the  include
include  . Together these give four possible tickets, which makes Professor Gamble’s probability
. Together these give four possible tickets, which makes Professor Gamble’s probability  .
. -
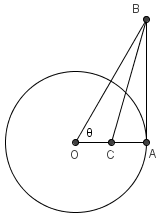
Solution 1
Since
 are all radii, it follows that
are all radii, it follows that  is an equilateral triangle.
is an equilateral triangle.
Draw the circle with center and radius
and radius  . Then let
. Then let  be the point of tangency of the two circles, and
be the point of tangency of the two circles, and  be the intersection of the smaller circle and
be the intersection of the smaller circle and  . Let
. Let  be the intersection of the smaller circle and
be the intersection of the smaller circle and  . Also define the radii
. Also define the radii  (note that
(note that  is a diameter of the smaller circle, as
is a diameter of the smaller circle, as  is the point of tangency of both circles, the radii of a circle is perpendicular to the tangent, hence the two centers of the circle are collinear with each other and
is the point of tangency of both circles, the radii of a circle is perpendicular to the tangent, hence the two centers of the circle are collinear with each other and  ).
).
By the Power of a Point Theorem,![[AF^2 = AE cdot AD Longrightarrow left(frac {r_1}2right)^2 = (AD - 2r_2) cdot AD.]](https://latex.artofproblemsolving.com/f/5/0/f502c8c08d3dcbccc056f8a854c51600e3ee9331.png) Since
Since  , then
, then  . Since
. Since  is equilateral,
is equilateral,  , and so
, and so  . Thus
. Thus  and the circumference of the circle is
and the circumference of the circle is  .
.
(Alternatively, the Pythagorean Theorem can also be used to find in terms of
in terms of  . Notice that since AB is tangent to circle
. Notice that since AB is tangent to circle  ,
,  is perpendicular to
is perpendicular to  . Therefore,
. Therefore, ![[AF^2 + OF^2 = AO^2]](https://latex.artofproblemsolving.com/f/1/d/f1da90b18af8980ff96aea8d68e9913060916564.png)
![[left(frac {r_1}{2}right)^2 + r_2^2 = (r_1 - r_2)^2]](https://latex.artofproblemsolving.com/c/7/f/c7f1d1ac3582d7813ce65354cfb304094b1323bf.png) After simplification,
After simplification,  .
.Solution 2 (Pythagorean Theorem)
First, note the triangle
 is equilateral. Next, notice that since the arc
is equilateral. Next, notice that since the arc  has length 12, it follows that we can find the radius of the sector centered at
has length 12, it follows that we can find the radius of the sector centered at  .
.  . Next, connect the center of the circle to side
. Next, connect the center of the circle to side  , and call this length
, and call this length  , and call the foot
, and call the foot  . Since
. Since  is equilateral, it follows that
is equilateral, it follows that  , and
, and  (where O is the center of the circle) is
(where O is the center of the circle) is  . By the pythagorean theorem, you get
. By the pythagorean theorem, you get  . Finally, we see that the circumference is
. Finally, we see that the circumference is  .
. -
Solution 1
Since the octahedron is indistinguishable by rotations, without loss of generality fix a face to be red.
![[asy] size(8cm); defaultpen(0.5); import three; import math; currentprojection=orthographic(2,0.2,1); triple A=(0,0,1); triple B=(sqrt(2)/2,sqrt(2)/2,0); triple C=(sqrt(2)/2,-sqrt(2)/2,0); triple D=(-sqrt(2)/2,-sqrt(2)/2,0); triple E=(-sqrt(2)/2,sqrt(2)/2,0); triple F=(0,0,-1); draw(A--B--E--cycle); draw(A--C--D--cycle); draw(F--C--B--cycle); draw(F--D--E--cycle,dotted+linewidth(0.7)); draw(surface(A--B--C--cycle),rgb(1,.6,.6),nolight);[/asy]](https://latex.artofproblemsolving.com/c/8/8/c88f77cd1f47ea3987a524e0a913959944cddccc.png) There are
There are  ways to arrange the remaining seven colors, but there still are three possible rotations about the fixed face, so the answer is
ways to arrange the remaining seven colors, but there still are three possible rotations about the fixed face, so the answer is  .
.![[asy] size(8cm); defaultpen(0.5); import three; import math; currentprojection=orthographic(2,0,1); triple A=(0,0,1); triple B=(sqrt(2)/2,sqrt(2)/2,0); triple C=(sqrt(2)/2,-sqrt(2)/2,0); triple D=(-sqrt(2)/2,-sqrt(2)/2,0); triple E=(-sqrt(2)/2,sqrt(2)/2,0); triple F=(0,0,-1); triple right=(0,1,0); picture p = new picture, r = new picture, s = new picture; draw(p,A--B--E--cycle); draw(p,A--C--D--cycle); draw(p,F--C--B--cycle); draw(p,F--D--E--cycle,dotted+linewidth(0.7)); draw(p,surface(A--B--C--cycle),rgb(1,.6,.6),nolight); draw(p,surface(A--B--E--cycle),rgb(1,1,.6),nolight); add(scale3(2.2)*p); draw(r,A--B--E--cycle); draw(r,A--C--D--cycle); draw(r,F--C--B--cycle); draw(r,F--D--E--cycle,dotted+linewidth(0.7)); draw(r,surface(A--B--C--cycle),rgb(1,.6,.6),nolight); draw(r,surface(A--C--D--cycle),rgb(1,1,.6),nolight); add(scale3(2.2)*shift(2*right)*r); draw(s,A--B--E--cycle); draw(s,A--C--D--cycle); draw(s,F--C--B--cycle); draw(s,F--D--E--cycle,dotted+linewidth(0.7)); draw(s,surface(A--B--C--cycle),rgb(1,.6,.6),nolight); draw(s,surface(B--C--F--cycle),rgb(1,1,.6),nolight); add(scale3(2.2)*shift(4*right)*s); [/asy]](https://latex.artofproblemsolving.com/1/3/7/13794d70fed69662b0c55408d02766344a410c75.png)
Solution 2
We consider the dual of the octahedron, the cube; a cube can be inscribed in an octahedron with each of its vertices at a face of the octahedron. So the problem is equivalent to finding the number of ways to color the vertices of a cube.
Select any vertex and call it ; there are
; there are  color choices for this vertex, but this vertex can be rotated to any of
color choices for this vertex, but this vertex can be rotated to any of  locations. After fixing
locations. After fixing  , we pick another vertex
, we pick another vertex  adjacent to
adjacent to  . There are seven color choices for
. There are seven color choices for  , but there are only three locations to which
, but there are only three locations to which  can be rotated to (since there are three edges from
can be rotated to (since there are three edges from  ). The remaining six vertices can be colored in any way and their locations are now fixed. Thus the total number of ways is
). The remaining six vertices can be colored in any way and their locations are now fixed. Thus the total number of ways is  .
.Solution 3
There are 8! ways to place eight colors on a fixed octahedron. An octahedron has six vertices, of which one can face the top, and for any vertex that faces the top, there are four different triangles around that vertex that can be facing you. Thus there are 6*4 = 24 ways to orient an octahedron, and

学术活动报名扫码了解!免费领取历年真题!
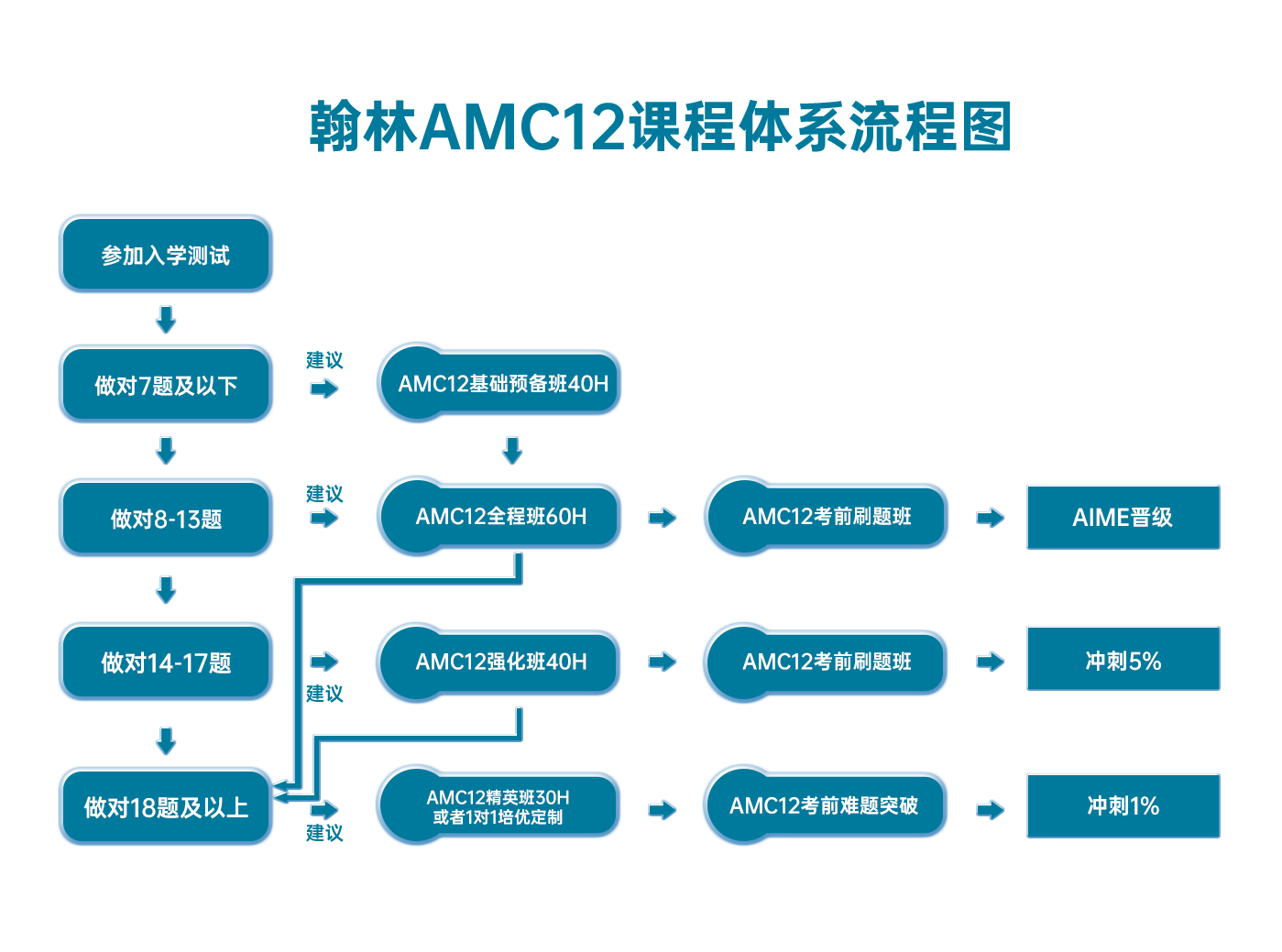
翰林AMC12课程体系流程图

最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1