1991 AMC8真题及答案详解
1991 AMC 8 真题
答案详细解析请参考文末
Problem 1
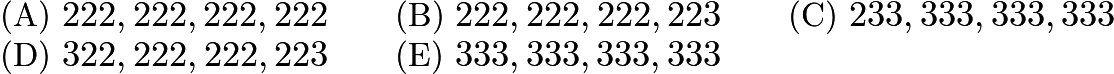
Problem 2
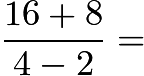
Problem 3
Two hundred thousand times two hundred thousand equals
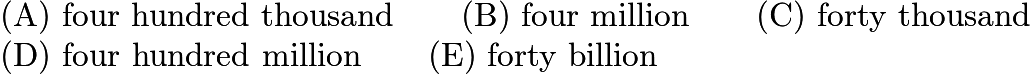
Problem 4
If 
, then 
Problem 5
A "domino" is made up of two small squares:
Which of the "checkerboards" illustrated below CANNOT be covered exactly and completely by a whole number of non-overlapping dominoes?
Problem 6
Which number in the array below is both the largest in its column and the smallest in its row? (Columns go up and down, rows go right and left.)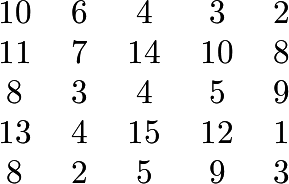
Problem 7
The value of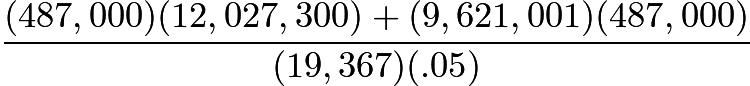 
is closest to
Problem 8
What is the largest quotient that can be formed using two numbers chosen from the set 
?
Problem 9
How many whole numbers from 
through 
are divisible by either 
or 
or both?
Problem 10
The area in square units of the region enclosed by parallelogram 
is
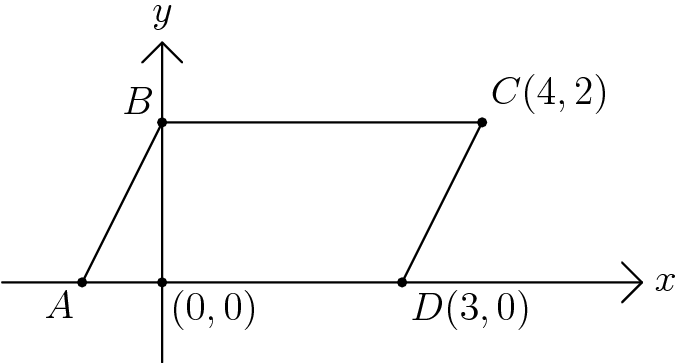
Problem 11
There are several sets of three different numbers whose sum is 
which can be chosen from 
. How many of these sets contain a ?
Problem 12
If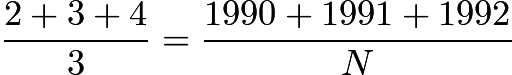 
, then
Problem 13
How many zeros are at the end of the product
Problem 14
Several students are competing in a series of three races. A student earns points for winning a race, points for finishing second and point for finishing third. There are no ties. What is the smallest number of points that a student must earn in the three races to be guaranteed of earning more points than any other student?
Problem 15
All six sides of a rectangular solid were rectangles. A one-foot cube was cut out of the rectangular solid as shown. The total number of square feet in the surface of the new solid is how many more or less than that of the original solid?
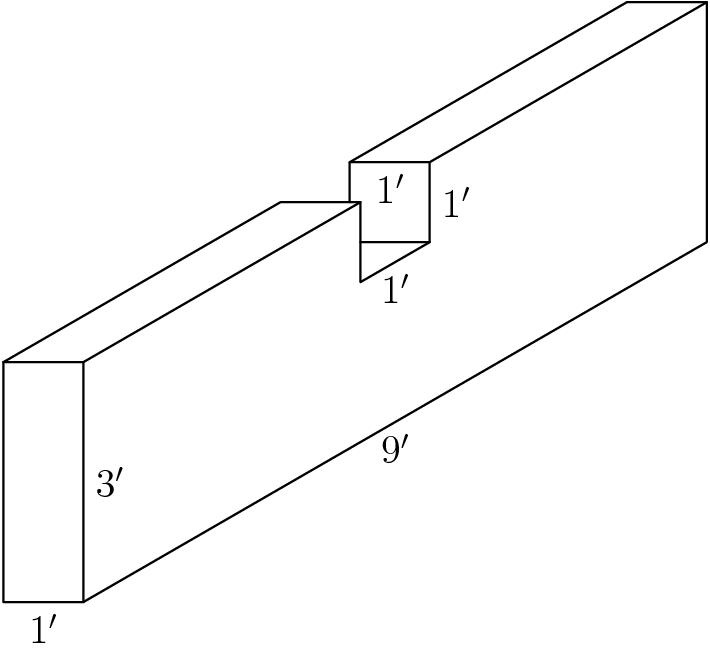
Problem 16
The 
squares on a piece of paper are numbered as shown in the diagram. While lying on a table, the paper is folded in half four times in the following sequence:
(1) fold the top half over the bottom half
(2) fold the bottom half over the top half
(3) fold the right half over the left half
(4) fold the left half over the right half.
Which numbered square is on top after step 
?
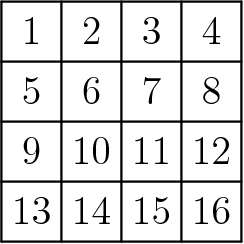
Problem 17
An auditorium with 
rows of seats has 
seats in the first row. Each successive row has one more seat than the previous row. If students taking an exam are permitted to sit in any row, but not next to another student in that row, then the maximum number of students that can be seated for an exam is
Problem 18
The vertical axis indicates the number of employees, but the scale was accidentally omitted from this graph. What percent of the employees at the Gauss company have worked there for years or more?
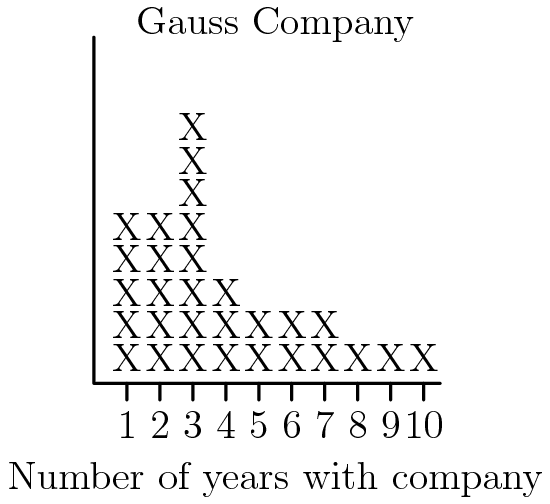
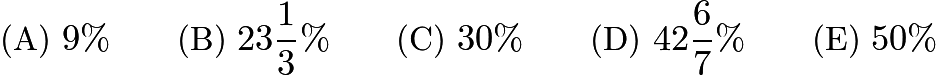
Problem 19
The average (arithmetic mean) of different positive whole numbers is . The largest possible value of any of these numbers is
Problem 20
In the addition problem, each digit has been replaced by a letter. If different letters represent different digits then 
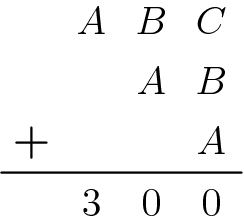
Problem 21
For every 
rise in temperature, the volume of a certain gas expands by cubic centimeters. If the volume of the gas is 
cubic centimeters when the temperature is 
, what was the volume of the gas in cubic centimeters when the temperature was 
?
Problem 22
Each spinner is divided into equal parts. The results obtained from spinning the two spinners are multiplied. What is the probability that this product is an even number?
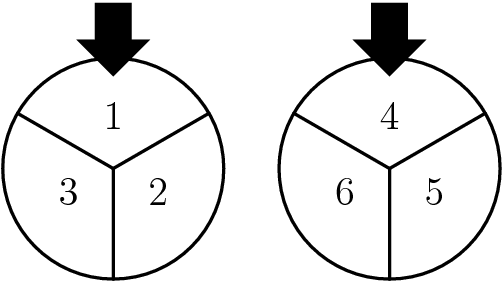
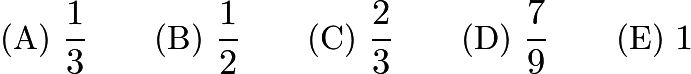
Problem 23
The Pythagoras High School band has 
female and 
male members. The Pythagoras High School orchestra has female and male members. There are 
females who are members in both band and orchestra. Altogether, there are 
students who are in either band or orchestra or both. The number of males in the band who are NOT in the orchestra is
Problem 24
A cube of edge cm is cut into 
smaller cubes, not all the same size. If the edge of each of the smaller cubes is a whole number of centimeters, then
Problem 25
An equilateral triangle is originally painted black. Each time the triangle is changed, the middle fourth of each black triangle turns white. After five changes, what fractional part of the original area of the black triangle remains black?
1991 AMC8真答案详细解析
1.
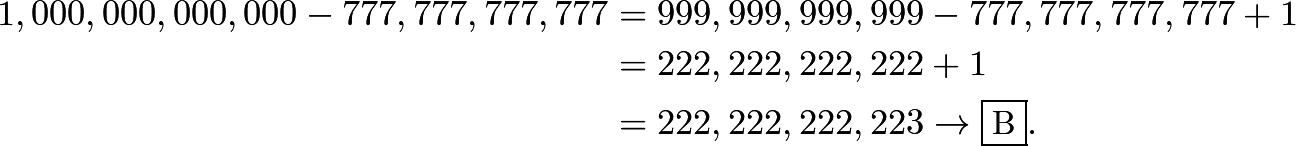
2.
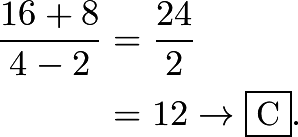
3.Writing the numbers in scientific notation, we have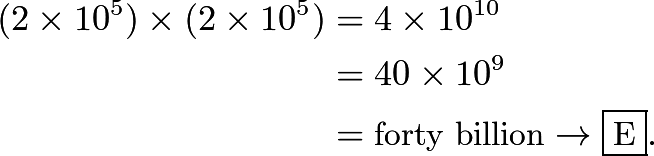
4.
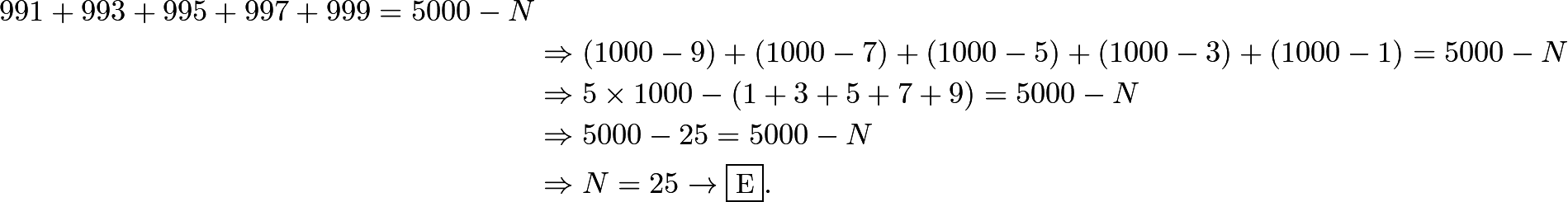
5.For a bunch of dominoes to completely tile a board, the board must have an even number of squares. The 
board clearly does not, so 
cannot be tiled completely.
6.The largest numbers in the first, second, third, fourth and fifth columns are 
respectively. Of these, only 
is the smallest in its row 
.
7.
We can make the approximations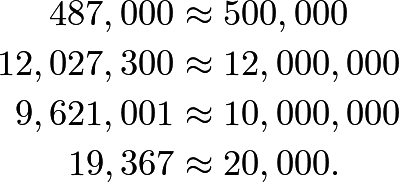
Using these instead of the original numbers for an estimate, we have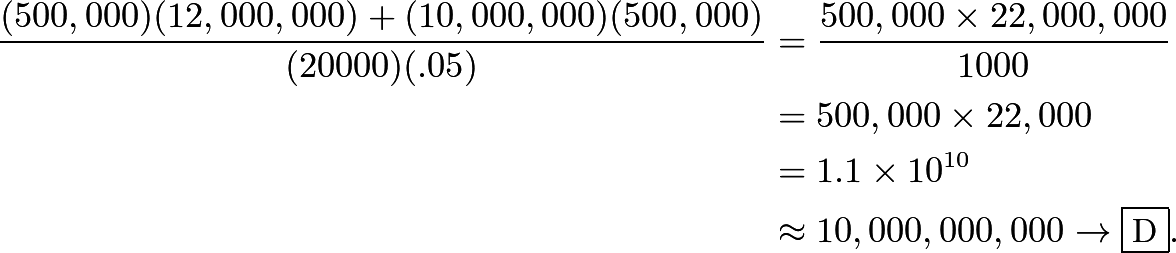
~*If you typed this into a calculator or actually got the answer, it would be AROUND 10 billion.*~
~*Calypso*~
8.
Let the two chosen numbers be 
and 
. To maximize the quotient, we first have either 
or 
, and from there we maximize 
and minimize 
.
For the case , we have 
and 
, which gives us 
. For the case , we have 
and 
, which gives us 
.
Since 
, our answer is 
.
9.
There are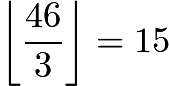 
numbers divisible by , 
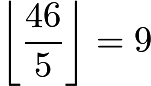numbers divisible by , so at first we have 
numbers that are divisible by or , except we counted the multiples of 
twice, once for and once for .
There are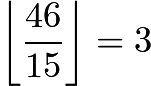 
numbers divisible by , so there are 
numbers divisible by or . 
10.The base is 
. The height has a length of the difference of the y-coordinates of A and B, which is 2. Therefore the area is 
.
11.
Let the three-element set be 
and suppose that 
.
We need 
and 
. This gives us four solutions, so there are sets with a also with the desired properties .
12.Note that for all integers 
,
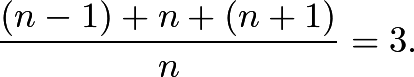Thus, we must have 
.
13.
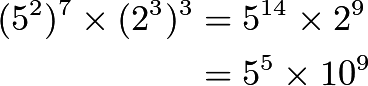Since 
doesn't end in a 
, we can conclude that the product ends in 
zeroes .
14.
There are two ways for a student to get 
: 
and 
. Clearly if someone gets one of these combinations someone else could get the other, so we are not guaranteed the most points with .
There is only one way to get 
points: 
. In this case, the largest score another person could get is 
, so having points guarantees having more points than any other person 
.
15.Initially, that one-foot cube contributed 3 faces to the surface area of the whole solid. When it was removed, these 3 faces are removed, but there are 3 new faces where the cube was carved out, so the net change is 
.
16.
Suppose we undo each of the four folds, considering just the top square until we completely unfold the paper. 
will be marked in the square if the face that shows after all the folds is face up, 
if that face is facing down.
Step 0:
Step 1: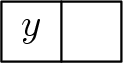
Step 2:
Step 3: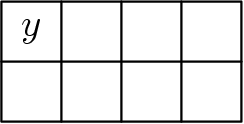
Step 4:
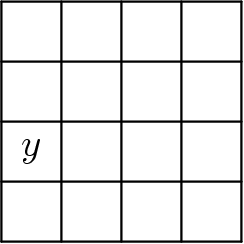The marked square is in the same spot as the number 
.
17.
We first note that if a row has 
seats, then the maximum number of students that can be seated in that row is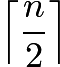 
, where 
is the smallest integer greater than or equal to . If a row has 
seats, clearly we can only fit 
students in that row. If a row has 
seats, we can fit 
students by putting students at the ends and then alternating between skipping a seat and putting a student in.
For each row with 
seats, there is a corresponding row with 
seats. The sum of the maximum number of students for these rows is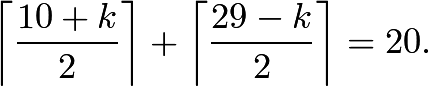
There are 
pairs of rows, so the maximum number of students for the exam is 
.
18.Let be the amount of people each 
represents. The percent of people that worked for five or more years is then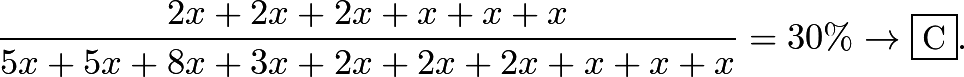
19.
If the average of the numbers is , then their sum is 
.
To maximize the largest number of the ten, we minimize the other nine. Since they must be distinct, positive whole numbers, we let them be 
. Their sum is 
.
The sum of nine of the numbers is , and the sum of all ten is so the last number must be 
.
20.
Solution
From this we have
Clearly, 
. Since 
,
Thus, 
and 
. From here it becomes clear that 
and 
.
Solution
Using logic, 
, therefore 
(from the carry over)
. So 
Thus, and . From here it becomes clear that and .
21.
We know that
Setting 
, we get the volume when the temperature is , which is 
.
22.
Instead of computing this probability directly, we can find the probability that the product is odd, and subtract that from .
The product of two integers is odd if and only if each of the two integers is odd. The probability the first spinner yields an odd number is 
and the probability the second spinner yields an odd number is 
, so the probability both yield an odd number is 
.
The desired probability is thus 
.
23.There are 
females in either band or orchestra, so there are 
males in either band or orchestra. Suppose males are in both band and orchestra. By PIE,
Thus, the number of males in band but not orchestra is 
.
24.
If none of the cubes have edge length 
, then all of the cubes have edge length , meaning they all are the same size, a contradiction.
It is clearly impossible to split a cube of edge into two or more cubes of edge with extra unit cubes, so there is one 
cube and 
unit cubes.
The total number of cubes, , is 
.
25.With each change, 
of the black space from the previous stage remains. Since there are changes, the fractional part of the triangle that remains black is 
.
以上解析方式仅供参考
学术活动报名扫码了解！免费领取历年真题！
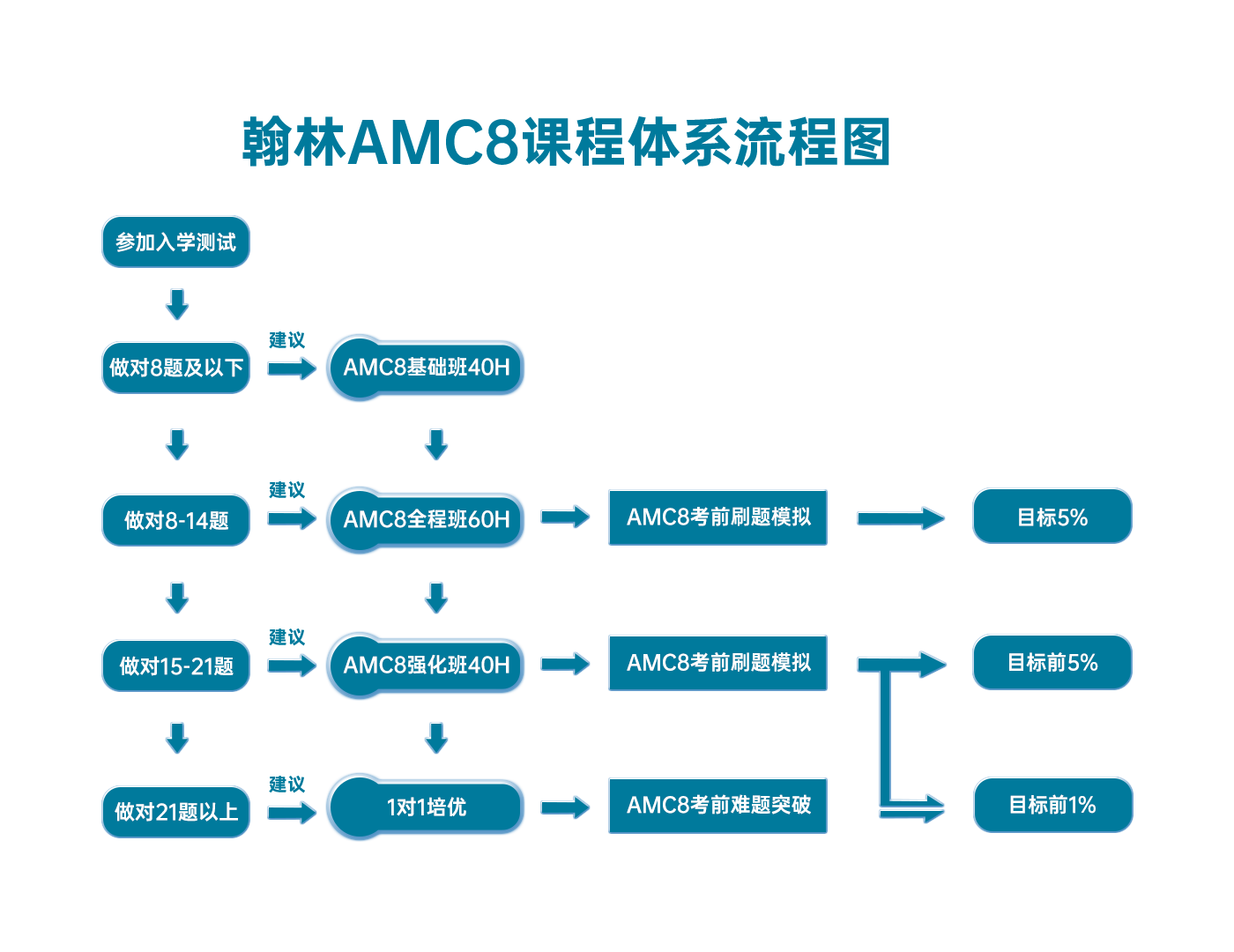
翰林AMC8课程体系流程图
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
