- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
1990 AMC8真题及答案详解
1990 AMC 8 真题
答案详细解析请参考文末
Problem 1
What is the smallest sum of two ![]() -digit numbers that can be obtained by placing each of the six digits
-digit numbers that can be obtained by placing each of the six digits ![]() in one of the six boxes in this addition problem?
in one of the six boxes in this addition problem?
![[asy] unitsize(12); draw((0,0)--(10,0)); draw((-1.5,1.5)--(-1.5,2.5)); draw((-1,2)--(-2,2)); draw((1,1)--(3,1)--(3,3)--(1,3)--cycle); draw((1,4)--(3,4)--(3,6)--(1,6)--cycle); draw((4,1)--(6,1)--(6,3)--(4,3)--cycle); draw((4,4)--(6,4)--(6,6)--(4,6)--cycle); draw((7,1)--(9,1)--(9,3)--(7,3)--cycle); draw((7,4)--(9,4)--(9,6)--(7,6)--cycle); [/asy]](https://latex.artofproblemsolving.com/9/1/4/914e5e0471d3dc0feff40587010f980154414e03.png)
![]()
Problem 2
Which digit of ![]() , when changed to
, when changed to ![]() , gives the largest number?
, gives the largest number?
![]()
Problem 3
What fraction of the square is shaded?
![[asy] draw((0,0)--(0,3)--(3,3)--(3,0)--cycle); draw((0,2)--(2,2)--(2,0)); draw((0,1)--(1,1)--(1,0)); draw((0,0)--(3,3)); fill((0,0)--(0,1)--(1,1)--cycle,grey); fill((1,0)--(1,1)--(2,2)--(2,0)--cycle,grey); fill((0,2)--(2,2)--(3,3)--(0,3)--cycle,grey); [/asy]](https://latex.artofproblemsolving.com/9/4/1/9418063c2f79f6fd1e9f8ec5e2efe31f98590f2f.png)
![]()
Problem 4
Which of the following could not be the unit's digit [one's digit] of the square of a whole number?
![]()
Problem 5
Which of the following is closest to the product ![]() ?
?
![]()
Problem 6
Which of these five numbers is the largest?
![]()
![]()
Problem 7
When three different numbers from the set ![]() are multiplied, the largest possible product is
are multiplied, the largest possible product is
![]()
Problem 8
A dress originally priced at ![]() dollars was put on sale for
dollars was put on sale for ![]() off. If
off. If ![]() tax was added to the sale price, then the total selling price (in dollars) of the dress was
tax was added to the sale price, then the total selling price (in dollars) of the dress was
![]()
Problem 9
The grading scale shown is used at Jones Junior High. The fifteen scores in Mr. Freeman's class were:![]()
In Mr. Freeman's class, what percent of the students received a grade of C?
![[boxed{begin{tabular}[t]{cc} A: & 93 - 100 \ B: & 85 - 92 \ C: & 75 - 84 \ D: & 70 - 74 \ F: & 0 - 69 end{tabular}}]](https://latex.artofproblemsolving.com/6/7/f/67f2dc5e3c44e79d79243fe5e8b62b3ca804f22f.png)
![]()
Problem 10
On this monthly calendar, the date behind one of the letters is added to the date behind ![]() . If this sum equals the sum of the dates behind
. If this sum equals the sum of the dates behind ![]() and
and ![]() , then the letter is
, then the letter is
![[asy] unitsize(12); draw((1,1)--(23,1)); draw((0,5)--(23,5)); draw((0,9)--(23,9)); draw((0,13)--(23,13)); for(int a=0; a<6; ++a) { draw((4a+2,0)--(4a+2,14)); } label("Tues.",(4,14),N); label("Wed.",(8,14),N); label("Thurs.",(12,14),N); label("Fri.",(16,14),N); label("Sat.",(20,14),N); label("C",(12,10.3),N); label("$textbf{A}$",(16,10.3),N); label("Q",(12,6.3),N); label("S",(4,2.3),N); label("$textbf{B}$",(8,2.3),N); label("P",(12,2.3),N); label("T",(16,2.3),N); label("R",(20,2.3),N); [/asy]](https://latex.artofproblemsolving.com/5/4/f/54ffff421c76ca2c5e63c918ddd6069e68ded4f7.png)
![]()
Problem 11
The numbers on the faces of this cube are consecutive whole numbers. The sums of the two numbers on each of the three pairs of opposite faces are equal. The sum of the six numbers on this cube is
![[asy] draw((0,0)--(3,0)--(3,3)--(0,3)--cycle); draw((3,0)--(5,2)--(5,5)--(2,5)--(0,3)); draw((3,3)--(5,5)); label("$15$",(1.5,1.2),N); label("$11$",(4,2.3),N); label("$14$",(2.5,3.7),N); [/asy]](https://latex.artofproblemsolving.com/1/b/1/1b1a85e70cc87bd44b6976f6eb76b21a969c7729.png)
![]()
Problem 12
There are twenty-four ![]() -digit numbers that use each of the four digits
-digit numbers that use each of the four digits ![]() ,
, ![]() ,
, ![]() , and
, and ![]() exactly once. Listed in numerical order from smallest to largest, the number in the
exactly once. Listed in numerical order from smallest to largest, the number in the ![]() position in the list is
position in the list is
![]()
Problem 13
One proposal for new postage rates for a letter was ![]() cents for the first ounce and
cents for the first ounce and ![]() cents for each additional ounce (or fraction of an ounce). The postage for a letter weighing
cents for each additional ounce (or fraction of an ounce). The postage for a letter weighing ![]() ounces was
ounces was
![]()
Problem 14
A bag contains only blue balls and green balls. There are ![]() blue balls. If the probability of drawing a blue ball at random from this bag is
blue balls. If the probability of drawing a blue ball at random from this bag is ![]() , then the number of green balls in the bag is
, then the number of green balls in the bag is
![]()
Problem 15
The area of this figure is ![]() . Its perimeter is
. Its perimeter is
![[asy] draw((0,2)--(2,2)--(2,1)--(3,1)--(3,0)--(1,0)--(1,1)--(0,1)--cycle,linewidth(1)); draw((1,2)--(1,1)--(2,1)--(2,0),dashed); [/asy]](https://latex.artofproblemsolving.com/4/b/8/4b8e9c1dd2a6fd8adac856d778af57eb39bc2aa3.png)
Problem 16
![]()
![]()
Problem 17
A straight concrete sidewalk is to be ![]() feet wide,
feet wide, ![]() feet long, and
feet long, and ![]() inches thick. How many cubic yards of concrete must a contractor order for the sidewalk if concrete must be ordered in a whole number of cubic yards?
inches thick. How many cubic yards of concrete must a contractor order for the sidewalk if concrete must be ordered in a whole number of cubic yards?
![]()
Problem 18
Each corner of a rectangular prism is cut off. Two (of the eight) cuts are shown. How many edges does the new figure have?
![[asy] draw((0,0)--(3,0)--(3,3)--(0,3)--cycle); draw((3,0)--(5,2)--(5,5)--(2,5)--(0,3)); draw((3,3)--(5,5)); draw((2,0)--(3,1.8)--(4,1)--cycle,linewidth(1)); draw((2,3)--(4,4)--(3,2)--cycle,linewidth(1)); [/asy]](https://latex.artofproblemsolving.com/f/a/5/fa5dea9ee182b4ce1bfdbb26fb958aa0e14ad235.png)
![]()
Assume that the planes cutting the prism do not intersect anywhere in or on the prism.
Problem 19
There are ![]() seats in a row. What is the fewest number of seats that must be occupied so the next person to be seated must sit next to someone?
seats in a row. What is the fewest number of seats that must be occupied so the next person to be seated must sit next to someone?
![]()
Problem 20
The annual incomes of ![]() families range from
families range from ![]() dollars to
dollars to ![]() dollars. In error, the largest income was entered on the computer as
dollars. In error, the largest income was entered on the computer as ![]() dollars. The difference between the mean of the incorrect data and the mean of the actual data is
dollars. The difference between the mean of the incorrect data and the mean of the actual data is
![]()
Problem 21
A list of ![]() numbers is formed by beginning with two given numbers. Each new number in the list is the product of the two previous numbers. Find the first number if the last three are shown:
numbers is formed by beginning with two given numbers. Each new number in the list is the product of the two previous numbers. Find the first number if the last three are shown:![]()
![]()
Problem 22
Several students are seated at a large circular table. They pass around a bag containing ![]() pieces of candy. Each person receives the bag, takes one piece of candy and then passes the bag to the next person. If Chris takes the first and last piece of candy, then the number of students at the table could be
pieces of candy. Each person receives the bag, takes one piece of candy and then passes the bag to the next person. If Chris takes the first and last piece of candy, then the number of students at the table could be
![]()
Problem 23
The graph relates the distance traveled [in miles] to the time elapsed [in hours] on a trip taken by an experimental airplane. During which hour was the average speed of this airplane the largest?
![[asy] unitsize(12); for(int a=1; a<13; ++a) { draw((2a,-1)--(2a,1)); } draw((-1,4)--(1,4)); draw((-1,8)--(1,8)); draw((-1,12)--(1,12)); draw((-1,16)--(1,16)); draw((0,0)--(0,17)); draw((-5,0)--(33,0)); label("$0$",(0,-1),S); label("$1$",(2,-1),S); label("$2$",(4,-1),S); label("$3$",(6,-1),S); label("$4$",(8,-1),S); label("$5$",(10,-1),S); label("$6$",(12,-1),S); label("$7$",(14,-1),S); label("$8$",(16,-1),S); label("$9$",(18,-1),S); label("$10$",(20,-1),S); label("$11$",(22,-1),S); label("$12$",(24,-1),S); label("Time in hours",(11,-2),S); label("$500$",(-1,4),W); label("$1000$",(-1,8),W); label("$1500$",(-1,12),W); label("$2000$",(-1,16),W); label(rotate(90)*"Distance traveled in miles",(-4,10),W); draw((0,0)--(2,3)--(4,7.2)--(6,8.5)); draw((6,8.5)--(16,12.5)--(18,14)--(24,15)); [/asy]](https://latex.artofproblemsolving.com/e/2/6/e26b6baebe0abf974115434df0f4732170d87518.png)
![]()
Problem 24
Three ![]() 's and a
's and a ![]() will balance nine
will balance nine ![]() 's. One
's. One ![]() will balance a
will balance a ![]() and a
and a ![]() .
.
![[asy] unitsize(5.5); fill((0,0)--(-4,-2)--(4,-2)--cycle,black); draw((-12,2)--(-12,0)--(12,0)--(12,2)); draw(ellipse((-12,5),8,3)); draw(ellipse((12,5),8,3)); label("$Delta hspace{2 mm}Delta hspace{2 mm}Delta hspace{2 mm}diamondsuit $",(-12,6.5),S); label("$bullet hspace{2 mm}bullet hspace{2 mm}bullet hspace{2 mm} bullet $",(12,5.2),N); label("$bullet hspace{2 mm}bullet hspace{2 mm}bullet hspace{2 mm}bullet hspace{2 mm}bullet $",(12,5.2),S); fill((44,0)--(40,-2)--(48,-2)--cycle,black); draw((34,2)--(34,0)--(54,0)--(54,2)); draw(ellipse((34,5),6,3)); draw(ellipse((54,5),6,3)); label("$Delta $",(34,6.5),S); label("$bullet hspace{2 mm}diamondsuit $",(54,6.5),S); [/asy]](https://latex.artofproblemsolving.com/2/1/b/21b669d079106f80b7d4285fa6df161d88a3182f.png)
How many ![]() 's will balance the two
's will balance the two ![]() 's in this balance?
's in this balance?
![[asy] unitsize(5.5); fill((0,0)--(-4,-2)--(4,-2)--cycle,black); draw((-12,4)--(-12,2)--(12,-2)--(12,0)); draw(ellipse((-12,7),6.5,3)); draw(ellipse((12,3),6.5,3)); label("$?$",(-12,8.5),S); label("$diamondsuit hspace{2 mm}diamondsuit $",(12,4.5),S); [/asy]](https://latex.artofproblemsolving.com/e/6/e/e6ef95632afcf6e191e1b0a65f22967b696978b7.png)
![]()
Problem 25
How many different patterns can be made by shading exactly two of the nine squares? Patterns that can be matched by flips and/or turns are not considered different. For example, the patterns shown below are not considered different.
![]()
![]()
1990 AMC8真答案详细解析
1.Let the two three-digit numbers be ![]() and
and ![]() . Their sum is equal to
. Their sum is equal to ![]() .
.
To minimize this, we need to minimize the contribution of the ![]() factor, so we let
factor, so we let ![]() and
and ![]() . Similarly, we let
. Similarly, we let ![]() ,
, ![]() , and then
, and then ![]() and
and ![]() . The sum is
. The sum is![]()
2.When dealing with positive decimals, the leftmost digits affect the change in value more. Thus, to get the largest number, we change the ![]() to a
to a ![]() .
.
3.Reflecting the square across the diagonal drawn, we see that the shaded region covers exactly the unshaded region in the original square, and thus makes up ![]() of the square
of the square ![]() .
.
4.We see that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , so already we know that either
, so already we know that either ![]() is the answer or the problem has some issues.
is the answer or the problem has some issues.
For integers, only the units digit affects the units digit of the final result, so we only need to test the squares of the integers from ![]() through
through ![]() inclusive. Testing shows that
inclusive. Testing shows that ![]() is unachievable, so the answer is
is unachievable, so the answer is ![]() .
.
5.
Solution 1
Clearly,![]() Since the function
Since the function ![]() is strictly increasing, we can say that
is strictly increasing, we can say that![]() from which it follows that
from which it follows that ![]() is much too small and
is much too small and ![]() is much too large, so
is much too large, so ![]() is the answer.
is the answer.
Solution 2
Since ![]() is quite close to
is quite close to ![]() , or
, or ![]() , we can look for the answer choice that is just below
, we can look for the answer choice that is just below ![]() , which would be
, which would be ![]() .
.
6.The options given in choices ![]() ,
, ![]() and
and ![]() don't change the initial value (13579) much, the option in choice
don't change the initial value (13579) much, the option in choice ![]() decreases 13579 by a lot, and the one given in choice
decreases 13579 by a lot, and the one given in choice ![]() increases 13579 by a lot.
increases 13579 by a lot.
After ensuring that no trivial error was made, we have ![]() as the answer.
as the answer.
7.First we try for a positive product, meaning we either pick three positive numbers or one positive number and two negative numbers.
It is clearly impossible to pick three positive numbers. If we try the second case, we want to pick the numbers with the largest absolute values, so we choose ![]() ,
, ![]() and
and ![]() . Their product is
. Their product is ![]() .
.
8.After the price reduction, the sale price is ![]() dollars. The tax makes the final price
dollars. The tax makes the final price ![]() dollars
dollars ![]() .
.
9.
We just count to find that there are ![]() students in the
students in the ![]() range.
range.
There are ![]() total, so the percentage is
total, so the percentage is ![]()
![]() .
.
10.Let the date behind ![]() be
be ![]() . Now the date behind
. Now the date behind ![]() is
is ![]() , and after looking at the calendar, the date behind
, and after looking at the calendar, the date behind ![]() is
is ![]() . Now we have
. Now we have ![]() for some date
for some date ![]() , and we desire for
, and we desire for ![]() to be
to be ![]() . Now we find that
. Now we find that ![]() is the date behind
is the date behind ![]() , so the answer is
, so the answer is ![]() ~motorfinn
~motorfinn
11.The only possibilities for the numbers are ![]() and
and ![]() .
.
In the second case, the common sum would be ![]() , so
, so ![]() must be paired with
must be paired with ![]() , which it isn't.
, which it isn't.
Thus, the only possibility is the first case and the sum of the six numbers is ![]() .
.
12.
For each choice of the thousands digit, there are ![]() numbers with that as the thousands digit. Thus, the six smallest are in the two thousands, the next six are in the four thousands, and then we need
numbers with that as the thousands digit. Thus, the six smallest are in the two thousands, the next six are in the four thousands, and then we need ![]() more numbers.
more numbers.
We can just list from here: ![]() .
.
13.
After the first ounce, there are ![]() ounces left. Since each additional ounce or fraction of an ounce adds
ounces left. Since each additional ounce or fraction of an ounce adds ![]() cents to the total cost, we need to add
cents to the total cost, we need to add ![]() to the cost for the first ounce.
to the cost for the first ounce.
So, the total price is ![]() cents. The answer is choice
cents. The answer is choice ![]() .
.
14.
Solution 1
The total number of balls in the bag must be ![]() , so there are
, so there are ![]() green balls
green balls ![]()
Solution 2
If b= number of blue balls in the bag and g = number of green balls in the bag then b/(b+g) = 1/4. Substituting b=6 and solving for g we get g=18, or B
- goldenn
15.
Since the area of the whole figure is ![]() , each square has an area of
, each square has an area of ![]() and the side length is
and the side length is ![]() .
.
There are ![]() sides of this length, so the perimeter is
sides of this length, so the perimeter is ![]() .
.
16.
In the middle, we have ![]() .
.
If we match up the back with the front, and then do the same for the rest, we get pairs with ![]() and
and ![]() , so these will cancel out. In the middle, we have
, so these will cancel out. In the middle, we have ![]() which doesn't cancel, but gives us
which doesn't cancel, but gives us ![]() .
.
17.This is a ![]() yard by
yard by ![]() yard by
yard by ![]() yard sidewalk, so its volume in yards is
yard sidewalk, so its volume in yards is![]() Since concrete must be ordered in a whole number of cubic yards, we need
Since concrete must be ordered in a whole number of cubic yards, we need ![]() .
.
18.
In addition to the original ![]() edges, each original vertex contributes
edges, each original vertex contributes ![]() new edges.
new edges.
There are ![]() original vertices, so there are
original vertices, so there are ![]() edges in the new figure
edges in the new figure ![]() .
.
19.
p is a person seated, o is an empty seat
The pattern of seating that results in the fewest occupied seats is opoopoopoo...po we can group the seats in 3s opo opo opo ... opo
there are a total of ![]() groups
groups
20.Let ![]() be the sum of all the incomes but the largest one. For the actual data, the mean is
be the sum of all the incomes but the largest one. For the actual data, the mean is ![]() , and for the incorrect data the mean is
, and for the incorrect data the mean is ![]() . The difference is
. The difference is ![]() .
.
21.We just use the definition to find the first number is ![]() .
.
22.If this is the case, then if there were only ![]() pieces of candy, the bag would have gone around the table a whole number of times. Thus, the number of students is a divisor of
pieces of candy, the bag would have gone around the table a whole number of times. Thus, the number of students is a divisor of ![]() . The only choice that satisfies this is choice
. The only choice that satisfies this is choice ![]() .
.
23.
The time when the average speed is greatest is when the slope of the graph is steepest. This is in the second hour ![]() .
.
24.
For simplicity, suppose ![]() ,
, ![]() and
and ![]() . Then,
. Then,![]()
![]() and we want to know what
and we want to know what ![]() is in terms of
is in terms of ![]() . Substituting the second equation into the first, we have
. Substituting the second equation into the first, we have![]()
Thus, we need ![]()
![]() 's
's ![]() .
.
25.
We break this into cases.
Case 1: At least one square is a vertex: WLOG, suppose one of them is in the upper-left corner. Then, consider the diagonal through that square. The two squares on that diagonal could be the second square, or the second square is on one side of the diagonal.
The square is reflectionally symmetric about this diagonal, so we only consider the squares on one side, giving another three possibilities.
In this case, there are ![]() distinct squares.
distinct squares.
Case 2: At least one square is on an edge, but no square is on a vertex: There are clearly two edge-edge combinations and one edge-center combination, so this case has ![]() squares.
squares.
In total, there are ![]() distinct squares
distinct squares ![]()
以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!
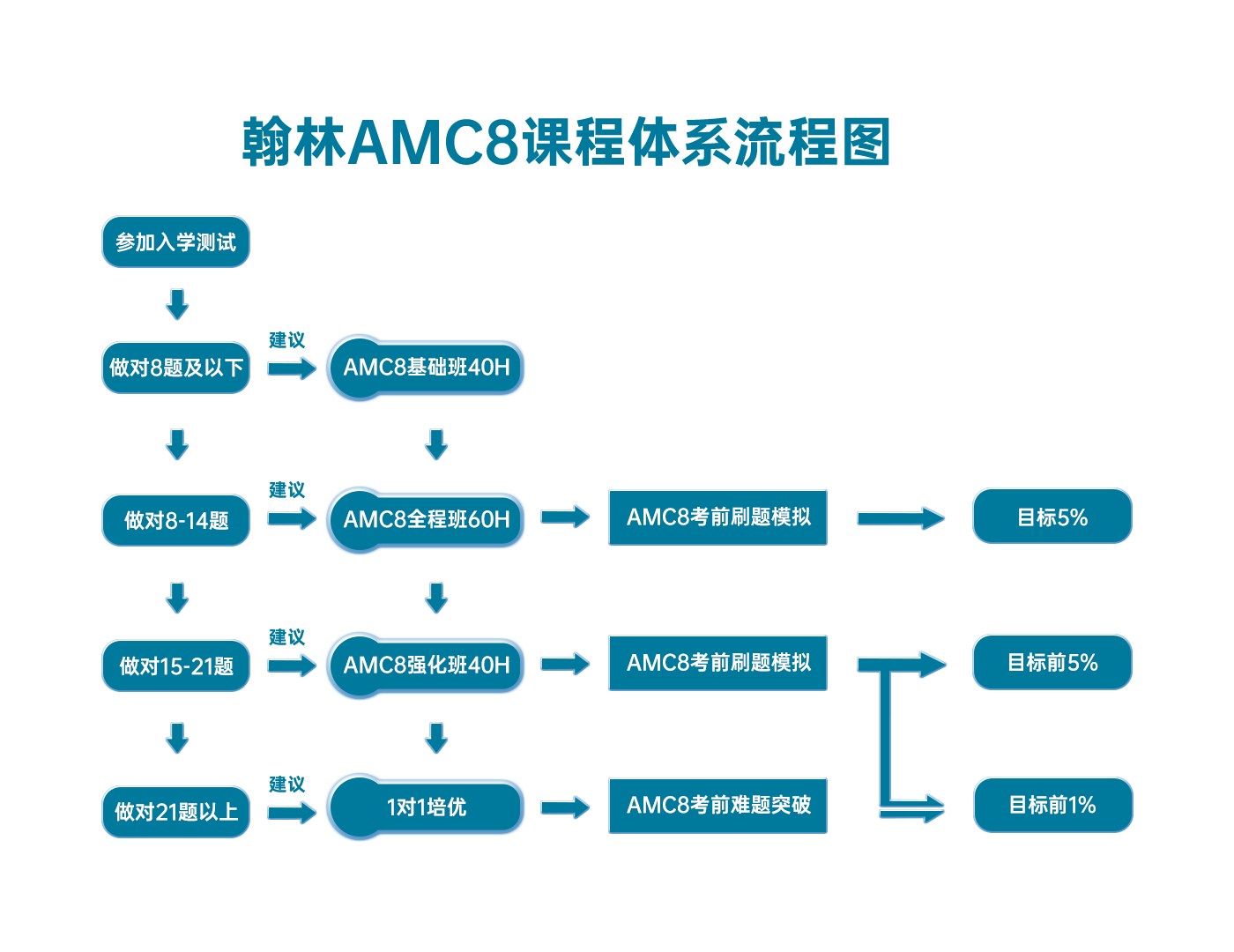
翰林AMC8课程体系流程图


最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








