Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

1998 AMC 8 真题及详解

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月4日下午12:42

1998 AMC 8 真题

答案详细解析请参考文末

Problem 1

For $x=7$ , which of the following is the smallest?

$text{(A)} dfrac{6}{x} qquad text{(B)} dfrac{6}{x+1} qquad text{(C)} dfrac{6}{x-1} qquad text{(D)} dfrac{x}{6} qquad text{(E)} dfrac{x+1}{6}$

Problem 2

If $begin{tabular}{r|l}a&b \ hline c&dend{tabular} = text{a}cdot text{d} - text{b}cdot text{c}$ , what is the value of $begin{tabular}{r|l}3&4 \ hline 1&2end{tabular}$ ?

$text{(A)} -2 qquad text{(B)} -1 qquad text{(C)} 0 qquad text{(D)} 1 qquad text{(E)} 2$

Problem 3

$dfrac{dfrac{3}{8} + dfrac{7}{8}}{dfrac{4}{5}} =$

$text{(A)} 1 qquad text{(B)} dfrac{25}{16} qquad text{(C)} 2 qquad text{(D)} dfrac{43}{20} qquad text{(E)} dfrac{47}{16}$

Problem 4

How many triangles are in this figure? (Some triangles may overlap other triangles.)

$[asy] draw((0,0)--(42,0)--(14,21)--cycle); draw((14,21)--(18,0)--(30,9)); [/asy]$

$text{(A)} 9 qquad text{(B)} 8 qquad text{(C)} 7 qquad text{(D)} 6 qquad text{(E)} 5$

Problem 5

Which of the following numbers is largest?

$text{(A)} 9.12344 qquad text{(B)} 9.123overline{4} qquad text{(C)} 9.12overline{34} qquad text{(D)} 9.1overline{234} qquad text{(E)} 9.overline{1234}$

Problem 6

Dots are spaced one unit apart, horizontally and vertically. The number of square units enclosed by the polygon is

$[asy] for(int a=0; a<4; ++a) { for(int b=0; b<4; ++b) { dot((a,b)); } } draw((0,0)--(0,2)--(1,2)--(2,3)--(2,2)--(3,2)--(3,0)--(2,0)--(2,1)--(1,0)--cycle); [/asy]$

$text{(A)} 5 qquad text{(B)} 6 qquad text{(C)} 7 qquad text{(D)} 8 qquad text{(E)} 9$

Problem 7

$100times 19.98times 1.998times 1000=$

$text{(A)} (1.998)^2 qquad text{(B)} (19.98)^2 qquad text{(C)} (199.8)^2 qquad text{(D)} (1998)^2 qquad text{(E)} (19980)^2$

Problem 8

A child's wading pool contains 200 gallons of water. If water evaporates at the rate of 0.5 gallons per day and no other water is added or removed, how many gallons of water will be in the pool after 30 days?

$text{(A)} 140 qquad text{(B)} 170 qquad text{(C)} 185 qquad text{(D)} 198.5 qquad text{(E)} 199.85$

Problem 9

For a sale, a store owner reduces the price of a $$$$ 10 scarf by $20%$ . Later the price is lowered again, this time by one-half the reduced price. The price is now

$text{(A)} 2.00text{ dollars} qquad text{(B)} 3.75text{ dollars} qquad text{(C)} 4.00text{ dollars} qquad text{(D)} 4.90text{ dollars} qquad text{(E)} 6.40text{ dollars}$

Problem 10

Each of the letters $text{W}$ , $text{X}$ , $text{Y}$ , and $text{Z}$ represents a different integer in the set ${ 1,2,3,4}$ , but not necessarily in that order. If $dfrac{text{W}}{text{X}} - dfrac{text{Y}}{text{Z}}=1$ , then the sum of $text{W}$ and $text{Y}$ is

$text{(A)} 3 qquad text{(B)} 4 qquad text{(C)} 5 qquad text{(D)} 6 qquad text{(E)} 7$

Problem 11

Harry has 3 sisters and 5 brothers. His sister Harriet has $text{S}$ sisters and $text{B}$ brothers. What is the product of $text{S}$ and $text{B}$ ?

$text{(A)} 8 qquad text{(B)} 10 qquad text{(C)} 12 qquad text{(D)} 15 qquad text{(E)} 18$

Problem 12

$2left(1-dfrac{1}{2}right) + 3left(1-dfrac{1}{3}right) + 4left(1-dfrac{1}{4}right) + cdots + 10left(1-dfrac{1}{10}right)=$

$text{(A)} 45 qquad text{(B)} 49 qquad text{(C)} 50 qquad text{(D)} 54 qquad text{(E)} 55$

Problem 13

What is the ratio of the area of the shaded square to the area of the large square? (The figure is drawn to scale)

$[asy] draw((0,0)--(0,4)--(4,4)--(4,0)--cycle); draw((0,0)--(4,4)); draw((0,4)--(3,1)--(3,3)); draw((1,1)--(2,0)--(4,2)); fill((1,1)--(2,0)--(3,1)--(2,2)--cycle,black); [/asy]$

$text{(A)} dfrac{1}{6} qquad text{(B)} dfrac{1}{7} qquad text{(C)} dfrac{1}{8} qquad text{(D)} dfrac{1}{12} qquad text{(E)} dfrac{1}{16}$

Problem 14

At Annville Junior High School, $30%$ of the students in the Math Club are in the Science Club, and $80%$ of the students in the Science Club are in the Math Club. There are 15 students in the Science Club. How many students are in the Math Club?

$text{(A)} 12 qquad text{(B)} 15 qquad text{(C)} 30 qquad text{(D)} 36 qquad text{(E)} 40$

Problem 15

Estimate the population of Nisos in the year 2050.

$text{(A)} 600 qquad text{(B)} 800 qquad text{(C)} 1000 qquad text{(D)} 2000 qquad text{(E)} 3000$

Problem 16

Estimate the year in which the population of Nisos will be approximately 6,000.

$text{(A)} 2050 qquad text{(B)} 2075 qquad text{(C)} 2100 qquad text{(D)} 2125 qquad text{(E)} 2150$

Problem 17

In how many years, approximately, from 1998 will the population of Nisos be as much as Queen Irene has proclaimed that the islands can support?

$text{(A)} 50text{ yrs.} qquad text{(B)} 75text{ yrs.} qquad text{(C)} 100text{ yrs.} qquad text{(D)} 125text{ yrs.} qquad text{(E)} 150text{ yrs.}$

Problem 18

As indicated by the diagram below, a rectangular piece of paper is folded bottom to top, then left to right, and finally, a hole is punched at X. What does the paper look like when unfolded?

$[asy] draw((2,0)--(2,1)--(4,1)--(4,0)--cycle); draw(circle((2.25,.75),.225)); draw((2.05,.95)--(2.45,.55)); draw((2.45,.95)--(2.05,.55)); draw((0,2)--(4,2)--(4,3)--(0,3)--cycle); draw((2,2)--(2,3),dashed); draw((1.3,2.1)..(2,2.3)..(2.7,2.1),EndArrow); draw((1.3,3.1)..(2,3.3)..(2.7,3.1),EndArrow); draw((0,4)--(4,4)--(4,6)--(0,6)--cycle); draw((0,5)--(4,5),dashed); draw((-.1,4.3)..(-.3,5)..(-.1,5.7),EndArrow); draw((3.9,4.3)..(3.7,5)..(3.9,5.7),EndArrow); [/asy]$

$[asy] unitsize(5); draw((0,0)--(16,0)--(16,8)--(0,8)--cycle); draw((0,4)--(16,4),dashed); draw((8,0)--(8,8),dashed); draw(circle((1,3),.9)); draw(circle((7,7),.9)); draw(circle((15,5),.9)); draw(circle((9,1),.9)); draw((24,0)--(40,0)--(40,8)--(24,8)--cycle); draw((24,4)--(40,4),dashed); draw((32,0)--(32,8),dashed); draw(circle((31,1),.9)); draw(circle((33,1),.9)); draw(circle((31,7),.9)); draw(circle((33,7),.9)); draw((48,0)--(64,0)--(64,8)--(48,8)--cycle); draw((48,4)--(64,4),dashed); draw((56,0)--(56,8),dashed); draw(circle((49,1),.9)); draw(circle((49,7),.9)); draw(circle((63,1),.9)); draw(circle((63,7),.9)); draw((72,0)--(88,0)--(88,8)--(72,8)--cycle); draw((72,4)--(88,4),dashed); draw((80,0)--(80,8),dashed); draw(circle((79,3),.9)); draw(circle((79,5),.9)); draw(circle((81,3),.9)); draw(circle((81,5),.9)); draw((96,0)--(112,0)--(112,8)--(96,8)--cycle); draw((96,4)--(112,4),dashed); draw((104,0)--(104,8),dashed); draw(circle((97,3),.9)); draw(circle((97,5),.9)); draw(circle((111,3),.9)); draw(circle((111,5),.9)); label("(A)",(8,10),N); label("(B)",(32,10),N); label("(C)",(56,10),N); label("(D)",(80,10),N); label("(E)",(104,10),N); [/asy]$

Problem 19

Tamika selects two different numbers at random from the set ${ 8,9,10 }$ and adds them. Carlos takes two different numbers at random from the set ${3, 5, 6}$ and multiplies them. What is the probability that Tamika's result is greater than Carlos' result?

$text{(A)} dfrac{4}{9} qquad text{(B)} dfrac{5}{9} qquad text{(C)} dfrac{1}{2} qquad text{(D)} dfrac{1}{3} qquad text{(E)} dfrac{2}{3}$

Problem 20

Let $PQRS$ be a square piece of paper. $P$ is folded onto $R$ and then $Q$ is folded onto $S$ . The area of the resulting figure is 9 square inches. Find the perimeter of square $PQRS$ .

$[asy] draw((0,0)--(2,0)--(2,2)--(0,2)--cycle); label("$P$",(0,2),SE); label("$Q$",(2,2),SW); label("$R$",(2,0),NW); label("$S$",(0,0),NE); [/asy]$

$text{(A)} 9 qquad text{(B)} 16 qquad text{(C)} 18 qquad text{(D)} 24 qquad text{(E)} 36$

Problem 21

A $4times 4times 4$ cubical box contains 64 identical small cubes that exactly fill the box. How many of these small cubes touch a side or the bottom of the box?

$text{(A)} 48 qquad text{(B)} 52 qquad text{(C)} 60 qquad text{(D)} 64 qquad text{(E)} 80$

Problem 22

Terri produces a sequence of positive integers by following three rules. She starts with a positive integer, then applies the appropriate rule to the result, and continues in this fashion.

Rule 1: If the integer is less than 10, multiply it by 9.

Rule 2: If the integer is even and greater than 9, divide it by 2.

Rule 3: If the integer is odd and greater than 9, subtract 5 from it.

A sample sequence: $23, 18, 9, 81, 76, ldots .$

Find the $98^text{th}$ term of the sequence that begins $98, 49, ldots .$

$text{(A)} 6 qquad text{(B)} 11 qquad text{(C)} 22 qquad text{(D)} 27 qquad text{(E)} 54$

Problem 23

If the pattern in the diagram continues, what fraction of the interior would be shaded in the eighth triangle?

$[asy] unitsize(10); draw((0,0)--(12,0)--(6,6sqrt(3))--cycle); draw((15,0)--(27,0)--(21,6sqrt(3))--cycle); fill((21,0)--(18,3sqrt(3))--(24,3sqrt(3))--cycle,black); draw((30,0)--(42,0)--(36,6sqrt(3))--cycle); fill((34,0)--(32,2sqrt(3))--(36,2sqrt(3))--cycle,black); fill((38,0)--(36,2sqrt(3))--(40,2sqrt(3))--cycle,black); fill((36,2sqrt(3))--(34,4sqrt(3))--(38,4sqrt(3))--cycle,black); draw((45,0)--(57,0)--(51,6sqrt(3))--cycle); fill((48,0)--(46.5,1.5sqrt(3))--(49.5,1.5sqrt(3))--cycle,black); fill((51,0)--(49.5,1.5sqrt(3))--(52.5,1.5sqrt(3))--cycle,black); fill((54,0)--(52.5,1.5sqrt(3))--(55.5,1.5sqrt(3))--cycle,black); fill((49.5,1.5sqrt(3))--(48,3sqrt(3))--(51,3sqrt(3))--cycle,black); fill((52.5,1.5sqrt(3))--(51,3sqrt(3))--(54,3sqrt(3))--cycle,black); fill((51,3sqrt(3))--(49.5,4.5sqrt(3))--(52.5,4.5sqrt(3))--cycle,black); [/asy]$ $text{(A)} dfrac{3}{8} qquad text{(B)} dfrac{5}{27} qquad text{(C)} dfrac{7}{16} qquad text{(D)} dfrac{9}{16} qquad text{(E)} dfrac{11}{45}$

Problem 24

A rectangular board of 8 columns has squares numbered beginning in the upper left corner and moving left to right so row one is numbered 1 through 8, row two is 9 through 16, and so on. A student shades square 1, then skips one square and shades square 3, skips two squares and shades square 6, skips 3 squares and shades square 10, and continues in this way until there is at least one shaded square in each column. What is the number of the shaded square that first achieves this result?

$[asy] unitsize(24); for(int a = 0; a < 10; ++a) { draw((0,a)--(8,a)); } for (int b = 0; b < 9; ++b) { draw((b,0)--(b,9)); } draw((0,0)--(0,-.5)); draw((1,0)--(1,-1.5)); draw((.5,-1)--(1.5,-1)); draw((2,0)--(2,-.5)); draw((4,0)--(4,-.5)); draw((5,0)--(5,-1.5)); draw((4.5,-1)--(5.5,-1)); draw((6,0)--(6,-.5)); draw((8,0)--(8,-.5)); fill((0,8)--(1,8)--(1,9)--(0,9)--cycle,black); fill((2,8)--(3,8)--(3,9)--(2,9)--cycle,black); fill((5,8)--(6,8)--(6,9)--(5,9)--cycle,black); fill((1,7)--(2,7)--(2,8)--(1,8)--cycle,black); fill((6,7)--(7,7)--(7,8)--(6,8)--cycle,black); label("$2$",(1.5,8.2),N); label("$4$",(3.5,8.2),N); label("$5$",(4.5,8.2),N); label("$7$",(6.5,8.2),N); label("$8$",(7.5,8.2),N); label("$9$",(0.5,7.2),N); label("$11$",(2.5,7.2),N); label("$12$",(3.5,7.2),N); label("$13$",(4.5,7.2),N); label("$14$",(5.5,7.2),N); label("$16$",(7.5,7.2),N); [/asy]$

$text{(A)} 36 qquad text{(B)} 64 qquad text{(C)} 78 qquad text{(D)} 91 qquad text{(E)} 120$

Problem 25

Three generous friends, each with some cash, redistribute their money as follows: Amy gives enough money to Jan and Toy to double the amount that each has. Jan then gives enough to Amy and Toy to double their amounts. Finally, Toy gives Amy and Jan enough to double their amounts. If Toy has $36 when they begin and $36 when they end, what is the total amount that all three friends have?

$text{(A)} 108text{ dollars} qquad text{(B)} 180text{ dollars} qquad text{(C)} 216text{ dollars} qquad text{(D)} 252text{ dollars} qquad text{(E)} 288text{ dollars}$

1998AMC8详细解析

The smallest fraction would be in the form $frac{a}{b}$ where $b$ is larger than $a$ .In this problem, we would need the largest possible value out of all the given values to be in the denominator. This value is $x+1$ or $8$ The smaller would go on the numerator, which is $6$ .The answer choice with $frac{6}{x+1}$ is $boxed{B}$ Plugging $x$ in for every answer choice would give $text{(A)} dfrac{6}{7} qquad text{(B)} dfrac{6}{8} qquad text{(C)} dfrac{6}{6} qquad text{(D)} dfrac{7}{6} qquad text{(E)} dfrac{8}{6}$ From here, we can see that the smallest is answer choice $boxed{B}$
Plugging in values for $a$ , $b$ , $c$ , and $d$ , we get $a=3$ , $b=4$ , $c=1$ , $d=2$ , $atimes d=3times2=6$ $btimes c=4times1=4$ $6-4=2$ $boxed{E}$
$frac{frac{3}{8}+frac{7}{8}}{frac{4}{5}} = frac{frac{10}{8}}{frac{4}{5}} = frac{frac{5}{4}}{frac{4}{5}} = frac{5}{4} cdot frac{5}{4} = frac{25}{16} = boxed{B}$
By inspection, we have that there $5$ triangles: Each of the $3$ small triangles, $1$ medium triangle made of the rightmost two small triangles, and the $1$ large triangle. $boxed{E}$
Looking at the different answer choices, we have (up to 10 digits after the decimal) $A$ : $9.1234400000$ $B$ : $9.1234444444$ $C$ : $9.1234343434$ $D$ : $9.1234234234$ $E$ : $9.1234123412$ By inspection, we can see that $boxed{B}$ is the largest number.
By inspection, you can notice that the triangle on the top row matches the hole in the bottom row.This creates a $2times3$ box, which has area $2times3=boxed{6}$ We could count the area contributed by each square on the $3 times 3$ grid:Top-left: $0$ Top: Triangle with area $frac{1}{2}$ Top-right: $0$ Left: Square with area $1$ Center: Square with area $1$ Right: Square with area $1$ Bottom-left: Square with area $1$
Bottom: Triangle with area $frac{1}{2}$

Bottom-right: Square with area $1$

Adding all of these together, we get $boxed{6}$ or $boxed{B}$

By Pick's Theorem, we get the formula, $A=I+frac{b}{2}-1$ where $I$ is the number of lattice points in the interior and $b$ being the number of lattice points on the boundary. In this problem, we can see that $I=1$ and $B=12$ . Substituting gives us $A=1+frac{12}{2}-1=6$ Thus, the answer is $boxed{text{(B) 6}}$
$19.98times100=1998$ $1.998times1000=1998$ $1998times1998=(1998)^2=boxed{D}$
$30$ days multiplied by $0.5$ gallons a day results in $15$ gallons of water loss.The remaining water is $200-15=185=boxed{C}$
$100%-20%=80%$ $10times80%=10times0.8$ $10times0.8=8$ $frac{8}{2}=4=boxed{C}$ The first discount has percentage 20, which is then discounted again for half of the already discounted price. $100-20=80$ $frac{80}{2}=40$ $40%times10=10times0.4=4=boxed{C}$
There are different ways to approach this problem, and I'll start with the different factor of the numbers of the set ${ 1,2,3,4}$ . $1$ has factor $1$ . $2$ has factors $1$ and $2$ $3$ has factors $1$ and $3$ $4$ has factors $1$ , $2$ , and $4$ .From here, we note that even though all numbers have the factor $1$ , only $4$ has another factor other than $1$ in the set (ie. $2$ )We could therefore have one fraction be $frac{4}{2}$ and another $frac{3}{1}$ .The sum of the numerators is $4+3=7=boxed{E}$
Harry has 3 sisters and 5 brothers. His sister, being a girl, would have 1 less sister and 1 more brother. $S = 3-1=2$ $B = 5+1=6$ $Scdot B = 2times6=12=boxed{C}$
Taking the first product, we have $left(1-frac{1}{2}right)=frac{1}{2}$ $frac{1}{2}times2=1$ Looking at the second, we get $left(1-frac{1}{3}right)=frac{2}{3}$ $frac{2}{3}times3=2$ We seem to be going up by $1$ .Just to check, $1-frac{1}{n}=frac{n-1}{n}$ $frac{n-1}{n}times n=n-1$
Now that we have discovered the pattern, we have to find the last term.

$1-frac{1}{10}=frac{9}{10}$

$frac{9}{10}times10=9$

The sum of all numbers from $1$ to $9$ is

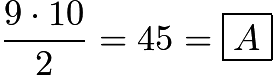
$frac{9cdot10}{2}=45=boxed{A}$
We can divide the large square into quarters by diagonals.Then, in $frac{1}{4}$ the area of the big square, the little square would have $frac{1}{2}$ the area. $frac{1}{4}timesfrac{1}{2}=frac{1}{8}=boxed{C}$ Answer: CDivide the square into 16 smaller squares as shown. The shaded square is formed from 4 half-squares, so its area is 2. The ratio 2 to 16 is 1/8.
If $80%$ of the people in the science club of $15$ people are in the Math Club, $frac{4}{5}times15=12$ people are in the both the Math Club and the Science Club.These $12$ people are also $30%$ of the Math Club.Setting up a proportion: $frac{12}{30%} = frac{x}{100%}$ $12cdot 1.00 =0.30cdot x$ $frac{12}{0.3} = 40=x$ There are $40=boxed{E}$ people in the Math Club.
The population triples every $25$ years from $200$ , and there are $50$ years between $2000$ and $2050$ , so we will have $200times3=600times3=1800$ .This is an underestimate, since there are actually $2$ more years for the island's population to grow.Therefore, $1800$ can be rounded to $2000=boxed{D}$
We could triple the population every $25$ years and make a chart:Year: 2000 Population: 200Year: 2025 Population: 600Year: 2050 Population: 1800Year: 2075 Population: 5400Year: 2100 Population: 16200The closest year is 2075, or $boxed{B}$ We could find out how many periods of 25 years we need to triple by dividing our total from our present number. $frac{6000}{200}=30$ The power of $3$ that $30$ is closest to is $27=3^3$
Therefore, after $3$ periods, we will be closest to $6000$ .

$boxed{B}$
We can divide the total area by how much will be occupied per person: $frac{24900 text{ acres}}{1.5 text{ acres per person}}=16600 text{ people}$ can stay on the island at its maximum capacity.We can divide this by the current population the island in the year $1998$ to see by what factor the population increases: $frac{16600}{200}=83$ -fold increase in population.Thus, the population increases by a factor $83$ . This is very close to $3 times 3 times 3 times 3 = 81$ , and so there are about $4$ triplings of the island's population.It takes $4times25=100=boxed{C}$ years to triple the island's population four times in succession.
By reversing the folds, we find that the holes will be1) In the middle (in relation from left to right)2) At separating poles (up and down)This is pictured in $boxed{B}$ If you unfold the paper, the hole you punched will not move. The only answer that keeps the hole in the upper-right quadrant in the same place is $boxed{B}$ .
The different possible (and equally likely) values Tamika gets are: $8+9=17$ $8+10=18$ $9+10=19$ The different possible (and equally likely) values Carlos gets are: $3times5=15$ $3times6=18$ $5times6=30$ The probability that if Tamika had the sum $17$ her sum would be greater than Carlos's set is $frac{1}{3}$ , because $17$ is only greater than $15$ The probability that if Tamika had the sum $18$ her sum would be greater than Carlos's set is $frac{1}{3}$ , because $18$ is only greater than $15$
The probability that if Tamika had the sum $19$ her sum would be greater than Carlos's set is $frac{2}{3}$ , because $19$ is greater than both $15$ and $18$

Each sum has a $frac{1}{3}$ possibility of being chosen, so we have

$frac{1}{3}left(frac{1}{3}+frac{1}{3}+frac{2}{3}right)=frac{1}{3}left(frac{4}{3}right)=frac{4}{9}=boxed{A}$
After both folds are completed, the square would become a triangle that has an area of $frac{1}{2} cdot frac{1}{2} = frac{1}{4}$ of the original square.Since the area is $9$ square inches for $frac{1}{4}$ of the square, $9times4=36$ square inches is the area of square $PQRS$ The length of the side of a square that has an area of $36$ square inches is $sqrt{36}=6$ inches.Each side is $6$ inches, so the total perimeter is $6times4=24=boxed{D}$
Each small cube would have dimensions $1times 1times 1$ making each cube a unit cube.If there are $16$ cubes per face and there are $5$ faces we are counting, we have $16times 5= 80$ cubes.Some cubes are on account of overlap between different faces.We could reduce this number by subtracting the overlap areas, which could mean subtracting 4 cubes from each side and 12 from the bottom. $80-(4times 4+12)=80-28=52=boxed{B}$ You can imagine removing the cubes that do not fit the description of the problem, forming a "square cup".There are $4$ cubes in the center of the top face that do not fit the description. Remove those.Once you remove those cubes on top, you must go down one level and remove the cubes in the same position on the second layer. Thus, $4$ more cubes are removed.Finally, you repeat this on the third layer, for $4$ more cubes.Once you do the top three layers, you will be on the bottom layer, and you don't remove any more cubes.
This means you removed $4 + 4 + 4 = 12$ cubes of the $4 times 4 times 4 = 64$ cubes.

Thus, $64 - 12 = 52$ cubes remain, and the answer is $boxed{B}$ .
We could start by looking for a pattern. $98, 49, 44, 22, 11, 6, 54, 27, 22, 11, 6, ldots .$ From here, we see that we have a pattern of $22, 11, 6, 54, 27, ldots .$ after $98, 49, 44$ Our problem is now reallyFind the $95^text{th}$ term of the sequence that goes $22, 11, 6, 54, 27, 22, 11, 6, 54, 27, 22, ldots .$ There are 5 terms in each repetition of the pattern, and $95equiv0pmod{5}$ , so the answer is $boxed{D}$
All small triangles are congruent in each iteration of the diagram. The number of shaded triangles follows the pattern: $0, 1, 3, 6, ...$ which is the pattern of "triangular numbers". Each time, the number $1, 2, 3, 4, 5...$ is added to the previous term. Thus, the first eight terms are: $0, 1, 3, 6, 10, 15, 21, 28$ In the eighth diagram, there will be $28$ shaded triangles.The total number of small triangles follows the pattern: $1, 4, 9, 16, ...$ which is the pattern of "square numbers". Thus, the eighth triangle will be divided into $8^2 = 64$ small triangles in total.The ratio of shaded to total triangles will be the fraction of the whole figure that's shaded, since all triangles are congruent. Thus, the answer is $frac{28}{64} = frac{7}{16}$ , and the correct choice is $boxed{C}$
The numbers that are shaded are the triangular numbers, which are numbers in the form $frac{(n)(n+1)}{2}$ for positive integers. They can also be generated by starting with $1$ , and adding $1, 2, 3, 4...$ as in the description of the problem.Squares that have the same remainder after being divided by $8$ will be in the same column. Thus, we want to find when the last remainder, from $0$ to $7$ , is found.So, instead of adding $1, 2, 3, 4, 5, 6, 7, 8, 9, 10...$ , we can effectively either add $1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3...$ or subtract $7, 6, 5, 4, 3, 2, 1, 0, 7, 6, 5...$ if we are only concerned about remainders when divided by $8$ . We will pick the number that keeps the terms on the list between $1$ and $8$ . We get: $1$ $1 + 2 = 3$ $3 + 3 = 6$ $6 - 4 = 2$ $2 + 5 = 7$ $7 - 2 = 5$ $5 - 1 = 4$
$4 + 0 = 4$

$4 + 1 = 5$

$5 + 2 = 7$

$7 - 5 = 2$

$2 + 4 = 6$

$6 - 3 = 3$

$3 - 2 = 1$

$1 - 1 = 0$

Finally, a term with $0$ is found, and checking, all numbers $1$ through $7$ are also on the right side of the list. This means the last term in our sequence is the first time that column $8$ is shaded. There are $15$ terms in the sequence, leading to an answer of $frac{15cdot 16}{2} = 120$ , which is choice $boxed{E}$ .

Note that the triangular numbers up to $120$ are $1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120$ . When you divide each of those numbers by $8$ , all remainders must be present. We first search for number(s) that are evenly divisible by $8$ ; if two such numbers exist, we search for numbers that leave a remainder of $1$ , etc.

Quickly scanning the list, only $6, 10, 28, 36, 66, 78$ and $120$ are even. That smaller list doesn't have any multiples of $8$ until it hits $120$ . So $boxed{120, E}$ must be the answer.

The numbers shaded are triangular numbers of the form $frac{(n)(n+1)}{2}$ . For this number to be divisible by $8$ , the numerator must be divisible by $16$ . Since only one of $n$ and $n+1$ can be even, only one of them can have factors of $2$ . Therefore, the first time the whole expression is divisible by $8$ is when either $n+1=16$ or when $n=16$ . This gives $n=15$ as the first time $frac{n(n+1)}{2}$ is divisible by $8$ , which gives $120$ . No other triangular number lower than that is divisible by $8$ , and thus the $8^{th}$ column on the checkerboard won't be filled until then. That gives $boxed{E}$ as the right answer.
If Toy had $36$ dollars at the beginning, then after Amy doubles his money, he has $36 times 2 = 72$ dollars after the first step.Then Jan doubles his money, and Toy has $72 times 2 = 144$ dollars after the second step.Then Toy doubles whatever Amy and Jan have. Since Toy ended up with $36$ , he spent $144 - 36 = 108$ to double their money. Therefore, just before this third step, Amy and Jan must have had $108$ dollars in total. And, just before this step, Toy had $144$ dollars. Altogether, the three had $144 + 108 = 252$ dollars, and the correct answer is $boxed{D}$