Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2000 AMC 8 真题及详解

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月4日下午12:08

2000 AMC 8 真题

答案详细解析请参考文末

Problem 1

Aunt Anna is $42$ years old. Caitlin is $5$ years younger than Brianna, and Brianna is half as old as Aunt Anna. How old is Caitlin?

$text{(A)} 15 qquad text{(B)} 16 qquad text{(C)} 17 qquad text{(D)} 21 qquad text{(E)} 37$

Problem 2

Which of these numbers is less than its reciprocal?

$text{(A)} -2 qquad text{(B)} -1 qquad text{(C)} 0 qquad text{(D)} 1 qquad text{(E)} 2$

Problem 3

How many whole numbers lie in the interval between $frac{5}{3}$ and $2pi?$

$text{(A)} 2 qquad text{(B)} 3 qquad text{(C)} 4 qquad text{(D)} 5 qquad text{(E)} text{infinitely many}$

Problem 4

In $1960$ only $5%$ of the working adults in Carlin City worked at home. By $1970$ the "at-home" work force increased to $8%$ . In $1980$ there were approximately $15%$ working at home, and in $1990$ there were $30%$ . The graph that best illustrates this is

$[asy] unitsize(18); draw((0,4)--(0,0)--(7,0)); draw((0,1)--(.2,1)); draw((0,2)--(.2,2)); draw((0,3)--(.2,3)); draw((2,0)--(2,.2)); draw((4,0)--(4,.2)); draw((6,0)--(6,.2)); for (int a = 1; a < 4; ++a) { for (int b = 1; b < 4; ++b) { draw((2*a,b-.1)--(2*a,b+.1)); draw((2*a-.1,b)--(2*a+.1,b)); } } label("1960",(0,0),S); label("1970",(2,0),S); label("1980",(4,0),S); label("1990",(6,0),S); label("10",(0,1),W); label("20",(0,2),W); label("30",(0,3),W); label("$%$",(0,4),N); draw((12,4)--(12,0)--(19,0)); draw((12,1)--(12.2,1)); draw((12,2)--(12.2,2)); draw((12,3)--(12.2,3)); draw((14,0)--(14,.2)); draw((16,0)--(16,.2)); draw((18,0)--(18,.2)); for (int a = 1; a < 4; ++a) { for (int b = 1; b < 4; ++b) { draw((2*a+12,b-.1)--(2*a+12,b+.1)); draw((2*a+11.9,b)--(2*a+12.1,b)); } } label("1960",(12,0),S); label("1970",(14,0),S); label("1980",(16,0),S); label("1990",(18,0),S); label("10",(12,1),W); label("20",(12,2),W); label("30",(12,3),W); label("$%$",(12,4),N); draw((0,12)--(0,8)--(7,8)); draw((0,9)--(.2,9)); draw((0,10)--(.2,10)); draw((0,11)--(.2,11)); draw((2,8)--(2,8.2)); draw((4,8)--(4,8.2)); draw((6,8)--(6,8.2)); for (int a = 1; a < 4; ++a) { for (int b = 1; b < 4; ++b) { draw((2*a,b+7.9)--(2*a,b+8.1)); draw((2*a-.1,b+8)--(2*a+.1,b+8)); } } label("1960",(0,8),S); label("1970",(2,8),S); label("1980",(4,8),S); label("1990",(6,8),S); label("10",(0,9),W); label("20",(0,10),W); label("30",(0,11),W); label("$%$",(0,12),N); draw((12,12)--(12,8)--(19,8)); draw((12,9)--(12.2,9)); draw((12,10)--(12.2,10)); draw((12,11)--(12.2,11)); draw((14,8)--(14,8.2)); draw((16,8)--(16,8.2)); draw((18,8)--(18,8.2)); for (int a = 1; a < 4; ++a) { for (int b = 1; b < 4; ++b) { draw((2*a+12,b+7.9)--(2*a+12,b+8.1)); draw((2*a+11.9,b+8)--(2*a+12.1,b+8)); } } label("1960",(12,8),S); label("1970",(14,8),S); label("1980",(16,8),S); label("1990",(18,8),S); label("10",(12,9),W); label("20",(12,10),W); label("30",(12,11),W); label("$%$",(12,12),N); draw((24,12)--(24,8)--(31,8)); draw((24,9)--(24.2,9)); draw((24,10)--(24.2,10)); draw((24,11)--(24.2,11)); draw((26,8)--(26,8.2)); draw((28,8)--(28,8.2)); draw((30,8)--(30,8.2)); for (int a = 1; a < 4; ++a) { for (int b = 1; b < 4; ++b) { draw((2*a+24,b+7.9)--(2*a+24,b+8.1)); draw((2*a+23.9,b+8)--(2*a+24.1,b+8)); } } label("1960",(24,8),S); label("1970",(26,8),S); label("1980",(28,8),S); label("1990",(30,8),S); label("10",(24,9),W); label("20",(24,10),W); label("30",(24,11),W); label("$%$",(24,12),N); draw((0,9)--(2,9.25)--(4,10)--(6,11)); draw((12,8.5)--(14,9)--(16,10)--(18,10.5)); draw((24,8.5)--(26,8.8)--(28,10.5)--(30,11)); draw((0,0.5)--(2,1)--(4,2.8)--(6,3)); draw((12,0.5)--(14,.8)--(16,1.5)--(18,3)); label("(A)",(-1,12),W); label("(B)",(11,12),W); label("(C)",(23,12),W); label("(D)",(-1,4),W); label("(E)",(11,4),W); [/asy]$

Problem 5

Each principal of Lincoln High School serves exactly one $3$ -year term. What is the maximum number of principals this school could have during an $8$ -year period?

$text{(A)} 2 qquad text{(B)} 3 qquad text{(C)} 4 qquad text{(D)} 5 qquad text{(E)} 8$

Problem 6

Figure $ABCD$ is a square. Inside this square three smaller squares are drawn with the side lengths as labeled. The area of the shaded $L$ -shaped region is

$[asy] pair A,B,C,D; A = (5,5); B = (5,0); C = (0,0); D = (0,5); fill((0,0)--(0,4)--(1,4)--(1,1)--(4,1)--(4,0)--cycle,gray); draw(A--B--C--D--cycle); draw((4,0)--(4,4)--(0,4)); draw((1,5)--(1,1)--(5,1)); label("$A$",A,NE); label("$B$",B,SE); label("$C$",C,SW); label("$D$",D,NW); label("$1$",(1,4.5),E); label("$1$",(0.5,5),N); label("$3$",(1,2.5),E); label("$3$",(2.5,1),N); label("$1$",(4,0.5),E); label("$1$",(4.5,1),N); [/asy]$

$text{(A)} 7 qquad text{(B)} 10 qquad text{(C)} 12.5 qquad text{(D)} 14 qquad text{(E)} 15$

Problem 7

What is the minimum possible product of three different numbers of the set ${-8,-6,-4,0,3,5,7}$ ?

$text{(A)} -336 qquad text{(B)} -280 qquad text{(C)} -210 qquad text{(D)} -192 qquad text{(E)} 0$

Problem 8

Three dice with faces numbered 1 through 6 are stacked as shown. Seven of the eighteen faces are visible, leaving eleven faces hidden (back, bottom, between). The total number of dots NOT visible in this view is

$[asy] draw((0,0)--(2,0)--(3,1)--(3,7)--(1,7)--(0,6)--cycle); draw((3,7)--(2,6)--(0,6)); draw((3,5)--(2,4)--(0,4)); draw((3,3)--(2,2)--(0,2)); draw((2,0)--(2,6)); dot((1,1)); dot((.5,.5)); dot((1.5,.5)); dot((1.5,1.5)); dot((.5,1.5)); dot((2.5,1.5)); dot((.5,2.5)); dot((1.5,2.5)); dot((1.5,3.5)); dot((.5,3.5)); dot((2.25,2.75)); dot((2.5,3)); dot((2.75,3.25)); dot((2.25,3.75)); dot((2.5,4)); dot((2.75,4.25)); dot((.5,5.5)); dot((1.5,4.5)); dot((2.25,4.75)); dot((2.5,5.5)); dot((2.75,6.25)); dot((1.5,6.5)); [/asy]$

$text{(A)} 21 qquad text{(B)} 22 qquad text{(C)} 31 qquad text{(D)} 41 qquad text{(E)} 53$

Problem 9

Three-digit powers of 2 and 5 are used in this cross-number puzzle. What is the only possible digit for the outlined square? $[begin{array}{lcl} textbf{ACROSS} & & textbf{DOWN} \ textbf{2}. 2^m & & textbf{1}. 5^n end{array}]$

$[asy] draw((0,-1)--(1,-1)--(1,2)--(0,2)--cycle); draw((0,1)--(3,1)--(3,0)--(0,0)); draw((3,0)--(2,0)--(2,1)--(3,1)--cycle,linewidth(2)); label("$1$",(0,2),SE); label("$2$",(0,1),SE); [/asy]$

$text{(A)} 0 qquad text{(B)} 2 qquad text{(C)} 4 qquad text{(D)} 6 qquad text{(E)} 8$

Problem 10

Ara and Shea were once the same height. Since then Shea has grown 20% while Ara has grown half as many inches as Shea. Shea is now 60 inches tall. How tall, in inches, is Ara now?

$text{(A)} 48 qquad text{(B)} 51 qquad text{(C)} 52 qquad text{(D)} 54 qquad text{(E)} 55$

Problem 11

The number 64 has the property that it is divisible by its units digit. How many whole numbers between 10 and 50 have this property?

$text{(A)} 15 qquad text{(B)} 16 qquad text{(C)} 17 qquad text{(D)} 18 qquad text{(E)} 20$

Problem 12

A block wall 100 feet long and 7 feet high will be constructed using blocks that are 1 foot high and either 2 feet long or 1 foot long (no blocks may be cut). The vertical joins in the blocks must be staggered as shown, and the wall must be even on the ends. What is the smallest number of blocks needed to build this wall?

$[asy] draw((0,0)--(6,0)--(6,1)--(5,1)--(5,2)--(0,2)--cycle); draw((0,1)--(5,1)); draw((1,1)--(1,2)); draw((3,1)--(3,2)); draw((2,0)--(2,1)); draw((4,0)--(4,1)); [/asy]$

$text{(A)} 344 qquad text{(B)} 347 qquad text{(C)} 350 qquad text{(D)} 353 qquad text{(E)} 356$

Problem 13

In triangle $CAT$ , we have $angle ACT = angle ATC$ and $angle CAT = 36^circ$ . If $overline{TR}$ bisects $angle ATC$ , then $angle CRT =$

$[asy] pair A,C,T,R; C = (0,0); T = (2,0); A = (1,sqrt(5+sqrt(20))); R = (3/2 - sqrt(5)/2,1.175570); draw(C--A--T--cycle); draw(T--R); label("$A$",A,N); label("$T$",T,SE); label("$C$",C,SW); label("$R$",R,NW); [/asy]$

$text{(A)} 36^circ qquad text{(B)} 54^circ qquad text{(C)} 72^circ qquad text{(D)} 90^circ qquad text{(E)} 108^circ$

Problem 14

What is the units digit of $19^{19} + 99^{99}$ ?

$text{(A)} 0 qquad text{(B)} 1 qquad text{(C)} 2 qquad text{(D)} 8 qquad text{(E)} 9$

Problem 15

Triangles $ABC$ , $ADE$ , and $EFG$ are all equilateral. Points $D$ and $G$ are midpoints of $overline{AC}$ and $overline{AE}$ , respectively. If $AB = 4$ , what is the perimeter of figure $ABCDEFG$ ?

$[asy] pair A,B,C,D,EE,F,G; A = (4,0); B = (0,0); C = (2,2*sqrt(3)); D = (3,sqrt(3)); EE = (5,sqrt(3)); F = (5.5,sqrt(3)/2); G = (4.5,sqrt(3)/2); draw(A--B--C--cycle); draw(D--EE--A); draw(EE--F--G); label("$A$",A,S); label("$B$",B,SW); label("$C$",C,N); label("$D$",D,NE); label("$E$",EE,NE); label("$F$",F,SE); label("$G$",G,SE); [/asy]$

$text{(A)} 12 qquad text{(B)} 13 qquad text{(C)} 15 qquad text{(D)} 18 qquad text{(E)} 21$

Problem 16

In order for Mateen to walk a kilometer (1000m) in his rectangular backyard, he must walk the length 25 times or walk its perimeter 10 times. What is the area of Mateen's backyard in square meters?

$text{(A)} 40 qquad text{(B)} 200 qquad text{(C)} 400 qquad text{(D)} 500 qquad text{(E)} 1000$

Problem 17

The operation $otimes$ is defined for all nonzero numbers by $aotimes b = dfrac{a^2}{b}$ . Determine $[(1otimes 2)otimes 3] - [1otimes (2otimes 3)]$ .

$text{(A)} -dfrac{2}{3} qquad text{(B)} -dfrac{1}{4} qquad text{(C)} 0 qquad text{(D)} dfrac{1}{4} qquad text{(E)} dfrac{2}{3}$

Problem 18

Consider these two geoboard quadrilaterals. Which of the following statements is true?

$[asy] for (int a = 0; a < 5; ++a) { for (int b = 0; b < 5; ++b) { dot((a,b)); } } draw((0,3)--(0,4)--(1,3)--(1,2)--cycle); draw((2,1)--(4,2)--(3,1)--(3,0)--cycle); label("I",(0.4,3),E); label("II",(2.9,1),W); [/asy]$

$text{(A)} text{The area of quadrilateral I is more than the area of quadrilateral II.}$

$text{(B)} text{The area of quadrilateral I is less than the area of quadrilateral II.}$

$text{(C)} text{The quadrilaterals have the same area and the same perimeter.}$

$text{(D)} text{The quadrilaterals have the same area, but the perimeter of I is more than the perimeter of II.}$

$text{(E)} text{The quadrilaterals have the same area, but the perimeter of I is less than the perimeter of II.}$

Problem 19

Three circular arcs of radius 5 units bound the region shown. Arcs $AB$ and $AD$ are quarter-circles, and arc $BCD$ is a semicircle. What is the area, in square units, of the region?

$[asy] pair A,B,C,D; A = (0,0); B = (-5,5); C = (0,10); D = (5,5); draw(arc((-5,0),A,B,CCW)); draw(arc((0,5),B,D,CW)); draw(arc((5,0),D,A,CCW)); label("$A$",A,S); label("$B$",B,W); label("$C$",C,N); label("$D$",D,E); [/asy]$

$text{(A)} 25 qquad text{(B)} 10 + 5pi qquad text{(C)} 50 qquad text{(D)} 50 + 5pi qquad text{(E)} 25pi$

Problem 20

You have nine coins: a collection of pennies, nickels, dimes, and quarters having a total value of $ $1.02$ , with at least one coin of each type. How many dimes must you have?

$text{(A)} 1 qquad text{(B)} 2 qquad text{(C)} 3 qquad text{(D)} 4 qquad text{(E)} 5$

Problem 21

Keiko tosses one penny and Ephraim tosses two pennies. The probability that Ephraim gets the same number of heads that Keiko gets is:

$text{(A)} dfrac{1}{4} qquad text{(B)} dfrac{3}{8} qquad text{(C)} dfrac{1}{2} qquad text{(D)} dfrac{2}{3} qquad text{(E)} dfrac{3}{4}$

Problem 22

A cube has edge length 2. Suppose that we glue a cube of edge length 1 on top of the big cube so that one of its faces rests entirely on the top face of the larger cube. The percent increase in the surface area (sides, top, and bottom) from the original cube to the new solid formed is closest to

$[asy] draw((0,0)--(2,0)--(3,1)--(3,3)--(2,2)--(0,2)--cycle); draw((2,0)--(2,2)); draw((0,2)--(1,3)); draw((1,7/3)--(1,10/3)--(2,10/3)--(2,7/3)--cycle); draw((2,7/3)--(5/2,17/6)--(5/2,23/6)--(3/2,23/6)--(1,10/3)); draw((2,10/3)--(5/2,23/6)); draw((3,3)--(5/2,3)); [/asy]$

$text{(A)} 10 qquad text{(B)} 15 qquad text{(C)} 17 qquad text{(D)} 21 qquad text{(E)} 25$

Problem 23

There is a list of seven numbers. The average of the first four numbers is 5, and the average of the last four numbers is 8. If the average of all seven numbers is $6frac{4}{7}$ , then the number common to both sets of four numbers is

$text{(A)} 5frac{3}{7} qquad text{(B)} 6 qquad text{(C)} 6frac{4}{7} qquad text{(D)} 7 qquad text{(E)} 7frac{3}{7}$

Problem 24

If $angle A = 20^circ$ and $angle AFG = angle AGF$ , then $angle B + angle D =$

$[asy] pair A,B,C,D,EE,F,G; A = (0,0); B = (9,4); C = (21,0); D = (13,-12); EE = (4,-16); F = (13/2,-6); G = (8,0); draw(A--C--EE--B--D--cycle); label("$A$",A,W); label("$B$",B,N); label("$C$",C,E); label("$D$",D,SE); label("$E$",EE,SW); label("$F$",F,WSW); label("$G$",G,NW); [/asy]$

$text{(A)} 48^circ qquad text{(B)} 60^circ qquad text{(C)} 72^circ qquad text{(D)} 80^circ qquad text{(E)} 90^circ$

Problem 25

The area of rectangle $ABCD$ is 72. If point $A$ and the midpoints of $overline{BC}$ and $overline{CD}$ are joined to form a triangle, the area of that triangle is

$[asy] pair A,B,C,D; A = (0,8); B = (9,8); C = (9,0); D = (0,0); draw(A--B--C--D--A--(9,4)--(4.5,0)--cycle); label("$A$",A,NW); label("$B$",B,NE); label("$C$",C,SE); label("$D$",D,SW); [/asy]$

$text{(A)} 21 qquad text{(B)} 27 qquad text{(C)} 30 qquad text{(D)} 36 qquad text{(E)} 40$

2000AMC8详细解析

If Brianna is half as old as Aunt Anna, then Briana is $frac{42}{2}$ years old, or $21$ years old.If Caitlin is $5$ years younger than Briana, she is $21-5$ years old, or $16$ .So, the answer is $boxed{B}$ Since Brianna is half of Aunt Anna's age this means that Brianna is $21$ years old. Now we just find Caitlin's age by doing $21-5$ . This makes $16$ or $boxed{B}$
The number $0$ has no reciprocal, and $1$ and $-1$ are their own reciprocals. This leaves only $2$ and $-2$ . The reciprocal of $2$ is $1/2$ , but $2$ is not less than $1/2$ . The reciprocal of $-2$ is $-1/2$ , and $-2$ is less than $-1/2$ , so it is $boxed{A}$ .The statement "a number is less than its reciprocal" can be translated as $x < frac{1}{x}$ .Multiplication by $x$ can be done if you do it in three parts: $x>0$ , $x=0$ , and $x<0$ . You have to be careful about the direction of the inequality, as you do not know the sign of $x$ .If $x>0$ , the sign of the inequality remains the same. Thus, we have $x^2 < 1$ when $x > 0$ . This leads to $0 < x < 1$ .
If $x=0$ , the inequality $x < frac{1}{x}$ is undefined.

If $x<0$ , the sign of the inequality must be switched. Thus, we have $x^2 > 1$ when $x < 0$ . This leads to $x < -1$ .

Putting the solutions together, we have $x<-1$ or $0 < x < 1$ , or in interval notation, $(-infty, -1) cup(0, 1)$ . The only answer in that range is $boxed {text{(A)} -2}$

Starting again with $x < frac{1}{x}$ , we avoid multiplication by $x$ . Instead, move everything to the left, and find a common denominator:

$x < frac{1}{x}$

$x - frac{1}{x} < 0$

$frac{x^2 - 1}{x} < 0$

$frac{(x+1)(x-1)}{x} < 0$

Divide this expression at $x=-1$ , $x=0$ , and $x=1$ , as those are the three points where the expression on the left will "change sign".

If $x<-1$ , all three of those terms will be negative, and the inequality is true. Therefore, $(-infty, -1)$ is part of our solution set.

If $-1 < x < 0$ , the $(x+1)$ term will become positive, but the other two terms remain negative. Thus, there are no solutions in this region.

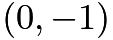If $0 < x < 1$ , then both $(x+1)$ and $x$ are positive, while $(x-1)$ remains negative. Thus, the entire region $(0, -1)$ is part of the solution set.

If $1 < x$ , then all three terms are positive, and there are no solutions.

At all three "boundary points", the function is either $0$ or undefined. Therefore, the entire solution set is $(-infty, -1) cup (0, 1)$ , and the only option in that region is $x=-2$ , leading to $boxed{A}$ .

We can find out all of their reciprocals. Now we compare and see that the answer is $boxed{A}$

Look at each number. Notice that the number must be negative. The number cannot be -1, 0, 1, ... . -2 is all that is left
The smallest whole number in the interval is $2$ because $5/3$ is more than $1$ but less than $2$ . The largest whole number in the interval is $6$ because $2pi$ is more than $6$ but less than $7$ . There are five whole numbers in the interval. They are $2$ , $3$ , $4$ , $5$ , and $6$ , so the answer is $boxed{text{(D)} 5}$ .We can approximate $2pi$ to $6$ . Now we approximate $5/3$ to $2$ . Now we list the integers between $2$ and $6$ including $2$ and $6$ : $[2,3,4,5,6]$ Hence, the answer is $boxed{D}$
The data are $1960 (5%)$ , $1970 (8%)$ , $1980 (15%)$ , and $1990 (30%)$ . Only one of these graphs has the answer and that is choice $boxed{E}$ .We can look at the graphs and note that the only one that has all the correct points is $boxed{E}$
If the first year of the $8$ -year period was the final year of a principal's term, then in the next six years two more principals would serve, and the last year of the period would be the first year of the fourth principal's term. Therefore, the maximum number of principals who can serve during an $8$ -year period is $4$ , so the answer is $boxed{C}$ if the terms are divided $1|2 3 4|5 6 7|8$
The side of the large square is $1 + 3 + 1 = 5$ , so the area of the large square is $5^2 = 25$ .The area of the middle square is $3^2$ , and the sum of the areas of the two smaller squares is $2 * 1^2 = 2$ .Thus, the big square minus the three smaller squares is $25 - 9 - 2 = 14$ . This is the area of the two congruent L-shaped regions.So the area of one L-shaped region is $frac{14}{2} = 7$ , and the answer is $boxed{A}$
The shaded area can be divided into three regions: one small square with side $1$ , and two rectangles with a length and width of $1$ and $3$ . The sum of these three areas is $1^2 + 3cdot 1 + 1cdot 3 = 1 + 3 + 3 = 7$ , and the answer is $boxed{A}$

The shaded area can be divided into two regions: one rectangle that is 1 by 3, and one rectangle that is 4 by 1. (Or the reverse, depending on which rectangle the 1 by 1 square is "joined" to.) Either way, the total area of these two regions is $3 + 4 = 7$ , and the answer is $boxed{A}$ .

Chop the entire 5 by 5 region into $25$ squares like a piece of graph paper. When you draw all the lines, you can count that only $7$ of the small 1 by 1 squares will be shaded, giving $boxed{A}$ as the answer.
The only way to get a negative product using three numbers is to multiply one negative number and two positives or three negatives. Only two reasonable choices exist: $(-8)times(-6)times(-4) = (-8)times(24) = -192$ and $(-8)times5times7 = (-8)times35 = -280$ . The latter is smaller, so $boxed{text{(B) -280}}$ .
The numbers on one die total $1+2+3+4+5+6 = 21$ , so the numbers on the three dice total $63$ . Numbers $1, 1, 2, 3, 4, 5, 6$ are visible, and these total $22$ . This leaves $63 - 22 = boxed{text{(D) 41}}$ not seen.
The $3$ -digit powers of $5$ are $125$ and $625$ , so space $2$ is filled with a $2$ . The only $3$ -digit power of $2$ beginning with $2$ is $256$ , so the outlined block is filled with a $boxed{text{(D) 6}}$ .
Shea has grown $20%$ , so she was originally $frac{60}{1.2}=50$ inches tall which is a $60 - 50 = 10$ inch increase. Ara also started off at $50$ inches. Since Ara grew half as much as Shea, Ara grew $10 div 2 = 5$ inches. Therefore, Ara is now $50+5=55$ inches tall which is choice $boxed{E}.$
Casework by the units digit $u$ will help organize the answer. $u=0$ gives no solutions, since no real numbers are divisible by $0$ $u=1$ has $4$ solutions, since all numbers are divisible by $1$ . $u=2$ has $4$ solutions, since every number ending in $2$ is even (ie divisible by $2$ ).
$u=3$ has $1$ solution: $33$ . $pm 10$ or $pm 20$ will retain the units digit, but will stop the number from being divisible by $3$ . $pm 30$ is the smallest multiple of $10$ that will keep the number divisible by $3$ , but those numbers are $3$ and $63$ , which are out of the range of the problem.

$u=4$ has $2$ solutions: $24$ and $44$ . Adding or subtracting $10$ will kill divisibility by $4$ , since $10$ is not divisible by $4$ .

$u=5$ has $4$ solutions: every number ending in $5$ is divisible by $5$ .

$u=6$ has $1$ solution: $36$ . $pm 10$ or $pm 20$ will kill divisibility by $3$ , and thus kill divisibility by $6$ .

$u=7$ has no solutions. The first multiples of $7$ that end in $7$ are $7$ and $77$ , but both are outside of the range of this problem.

$u=8$ has $1$ solution: $48$ . $pm 10, pm 20, pm 30$ will all kill divisibility by $8$ since $10, 20,$ and $30$ are not divisible by $8$ .

$u=9$ has no solutions. $9$ and $99$ are the smallest multiples of $9$ that end in $9$ .

Totalling the solutions, we have $0 + 4 + 4 + 1 + 2 + 4 + 1 + 0 + 1 + 0 = 17$ solutions, giving the answer $boxed{C}$
Since the bricks are $1$ foot high, there will be $7$ rows. To minimize the number of blocks used, rows $1, 3, 5,$ and $7$ will look like the bottom row of the picture, which takes $frac{100}{2} = 50$ bricks to construct. Rows $2, 4,$ and $6$ will look like the upper row pictured, which has $49$ 2-foot bricks in the middle, and $2$ 1-foot bricks on each end for a total of $51$ bricks.Four rows of $50$ bricks and three rows of $51$ bricks totals $4cdot 50 + 3cdot 51 = 200 + 153 = 353$ bricks, giving the answer $boxed{D}$
In $triangle ACT$ , the three angles sum to $180^circ$ , and $angle C = angle T$ $angle CAT + angle ATC + angle ACT = 180$ $36 + angle ATC + angle ATC = 180$ $2 angle ATC = 144$
$angle ATC = 72$

Since $angle ATC$ is bisected by $overline{TR}$ , $angle RTC = frac{72}{2} = 36$

Now focusing on the smaller $triangle RTC$ , the sum of the angles in that triangle is $180^circ$ , so:

$angle RTC + angle TCR + angle CRT = 180$

$36 + angle ACT + angle CRT = 180$

$36 + angle ATC + angle CRT = 180$

$36 + 72 + angle CRT = 180$

$angle CRT = 72^circ$ , giving the answer $boxed{C}$
Finding a pattern for each half of the sum, even powers of $19$ have a units digit of $1$ , and odd powers of $19$ have a units digit of $9$ . So, $19^{19}$ has a units digit of $9$ .Powers of $99$ have the exact same property, so $99^{99}$ also has a units digit of $9$ . $9+9=18$ which has a units digit of $8$ , so the answer is $boxed{D}$ .
The large triangle $ABC$ has sides of length $4$ . The medium triangle has sides of length $2$ . The small triangle has sides of length $1$ . There are $3$ segment sizes, and all segments depicted are one of these lengths.Starting at $A$ and going clockwise, the perimeter is: $AB + BC + CD + DE + EF + FG + GA$ $4 + 4 + 2 + 2 + 1 + 1 + 1$
$15$ , thus the answer is $boxed{C}$

The perimeter of $ABCDEFG$ is the perimeter of the three triangles, minus segments $AD$ and $EG$ , which are on the interior of the figure. Because each of these segments is on two triangles, each segment must be subtracted two times.

As in solution 1, the sides of the triangles are $4, 2,$ and $1$ , and the perimeters of the triangles are thus $12, 6,$ and $3$ .

The perimeter of the three triangles is $12 + 6 + 3 = 21$ . Subtracting the two segments $AD$ and $EG$ two times, the perimeter of $ABCDEFG$ is $21 - 2 - 1 - 2 - 1 = 15$ , and the answer is $boxed{C}$ .
The length $L$ of the rectangle is $frac{1000}{25}=40$ meters. The perimeter $P$ is $frac{1000}{10}=100$ meters. Since $P_{rect} = 2L + 2W$ , we plug values in to get: $100 = 2cdot 40 + 2W$ $100 = 80 + 2W$ $2W = 20$
$W = 10$ meters

Since $A_{rect} = LW$ , the area is $40cdot 10=400$ square meters or $boxed{C}$ .
Follow PE(MD)(AS), doing the innermost parentheses first. $[(1otimes 2)otimes 3]-[1otimes (2otimes 3)]$ $[frac{1^2}{2}otimes 3]-[1otimes frac{2^2}{3}]$ $[frac{1}{2}otimes 3]-[1otimes frac{4}{3}]$
$[frac{(frac{1}{2})^{2}}{3}]-[frac{1^2}{(frac{4}{3})}]$

$[frac{1}{4} cdot frac{1}{3}]-[frac{3}{4}]$

$frac{1}{12} - frac{3}{4}$

$frac{1}{12} - frac{9}{12}$

$frac{-8}{12}$

$-frac{2}{3}$ , which is answer $boxed{A}$
First consider the area of the two figures. Assume that the pegs are $1$ unit apart. Divide region I into two triangles by drawing a horizontal line on the second row from the top. Shifting the bottom triangle up one unit will create a square, and this square has the same area as region I. Thus, region I has an area of $1$ square unit.Draw a horizontal line on figure II on the fourth row from the top to divide the figure into two triangles. Temporarily move the top of the higher triangle one peg to the left. This will preserve the area of the triangle, as you are keeping both the height and the base of the triangle equal. Now you have two congruent triangles that are half of the area of a unit square. Thus, region II also has an area of $1$ square unit, and the areas are equal.To compare the perimeters, note that region I has two different side lengths: two sides are $1$ unit apart, and the other two sides are $sqrt{2}$ apart, as they are the diagonal of a unit square. The total perimeter is $2 + 2sqrt{2}$ .Note that region II has three different side lengths. One side is a unit length, while two sides are $sqrt{2}$ . For the perimeters to be equal, the last side must be of unit length. But the last side in region II is clearly longer than $1$ unit, so we can say that the perimeter of region II is greater than the perimeter of region I without calculating it.
Thus, the correct answer is $boxed{E}$ .

(The perimeter of region II is $1 + 2sqrt{2} + sqrt{5}$ , since the last side is the diagonal of a 2 by 1 rectangle, and can be found with the pythagorean theorem as $sqrt{2^2 + 1^2} = sqrt{5}$ . This does not need to be found for this problem, as you can do a one-to-one correspondance with three of the four sides of the figure as outlined, and just compare the last remaining side of each figure.)
Draw two squares: one that has opposing corners at $A$ and $B$ , and one that has opposing corners at $A$ and $D$ . These squares share side $overline{AO}$ , where $O$ is the center of the large semicircle.These two squares have a total area of $2 cdot 5^2$ , but have two quarter circle "bites" of radius $5$ that must be removed. Thus, the bottom part of the figure has area $2cdot 25 - 2 cdot frac{1}{4}pi cdot 5^2$ $50 - frac{25pi}{2}$
This is the area of the part of the figure underneath $overline{BD}$ . The part of the figure over $overline{BD}$ is just a semicircle with radius $5$ , which has area of $frac{1}{2}picdot 5^2 = frac{25pi}{2}$

Adding the two areas gives a total area of $50$ , for an answer of $boxed{C}$

Draw line $overline{BD}$ . Then draw $overline {CO}$ , where $O$ is the center of the semicircle. You have two quarter circles on top, and two quarter circle-sized "bites" on the bottom. Move the pieces from the top to fit in the bottom like a jigsaw puzzle. You now have a rectangle with length $overline {BD}$ and height $overline {AO}$ , which are equal to $10$ and $5$ , respectively. Thus, the total area is $50$ , and the answer is $boxed{C}$ .
Since you have one coin of each type, $1 + 5 + 10 + 25 = 41$ cents are already determined, leaving you with a total of $102 - 41 = 61$ cents remaining for $5$ coins.You must have $1$ more penny. If you had more than $1$ penny, you must have at least $6$ pennies to leave a multiple of $5$ for the nickels, dimes, and quarters. But you only have $5$ more coins to assign.Now you have $61 - 1 = 60$ cents remaining for $4$ coins, which may be nickels, quarters, or dimes. If you have only one more dime, that leaves $50$ cents in $3$ nickels or quarters, which is impossible. If you have two dimes, that leaves $40$ cents for $2$ nickels or quarters, which is again impossible. If you have three dimes, that leaves $30$ cents for $1$ nickel or quarter, which is still impossible. And all four remaining coins being dimes will not be enough.Therefore, you must have no more dimes to assign, and the $60$ cents in $4$ coins must be divided between the quarters and nickels. We quickly see that $2$ nickels and $2$ quarters work. Thus, the total count is $2$ quarters, $2$ nickels, $1$ penny, plus one more coin of each type that we originally subtracted. Double-checking, that gives a total $2 + 2 + 1 + 4 = 9$ coins, and a total of $2cdot 25 + 2cdot 5 + 1 + (1 + 5 + 10 + 25) = 102$ cents.
There is only $1$ dime in that combo, so the answer is $boxed{A}$ .
Let $K(n)$ be the probability that Keiko gets $n$ heads, and let $E(n)$ be the probability that Ephriam gets $n$ heads. $K(0) = frac{1}{2}$ $K(1) = frac{1}{2}$ $K(2) = 0$ (Keiko only has one penny!)
$E(0) = frac{1}{2}cdotfrac{1}{2} = frac{1}{4}$

$E(1) = frac{1}{2}cdotfrac{1}{2} + frac{1}{2}cdotfrac{1}{2} = 2cdotfrac{1}{4} = frac{1}{2}$ (because Ephraim can get HT or TH)

$E(2) = frac{1}{2}cdotfrac{1}{2} = frac{1}{4}$

The probability that Keiko gets $0$ heads and Ephriam gets $0$ heads is $K(0)cdot E(0)$ . Similarly for $1$ head and $2$ heads. Thus, we have:

$P = K(0)cdot E(0) + K(1)cdot E(1) + K(2)cdot E(2)$

$P = frac{1}{2}cdotfrac{1}{4} + frac{1}{2}cdotfrac{1}{2} + 0$

$P = frac{3}{8}$

Thus the answer is $boxed{B}$ .
The original cube has $6$ faces, each with an area of $2cdot 2 = 4$ square units. Thus the original figure had a total surface area of $24$ square units.The new figure has the original surface, with $6$ new faces that each have an area of $1$ square unit, for a total surface area of of $6$ additional square units added to it. But $1$ square unit of the top of the bigger cube, and $1$ square unit on the bottom of smaller cube, is not on the surface, and does not count towards the surface area.The total surface area is therefore $24 + 6 - 1 - 1 = 28$ square units.The percent increase in surface area is $frac{SA_{new} - SA_{old}}{SA_{old}}cdot 100% = frac{28-24}{24}cdot 100% approx 16.67%$ , giving the closest answer as $boxed{C}$ .
Remember that if a list of $n$ numbers has an average of $k$ , then the sum $S$ of all the numbers on the list is $S = nk$ .So if the average of the first $4$ numbers is $5$ , then the first four numbers total $4 cdot 5 = 20$ .If the average of the last $4$ numbers is $8$ , then the last four numbers total $4 cdot 8 = 32$ .If the average of all $7$ numbers is $6frac{4}{7}$ , then the total of all seven numbers is $7 cdot 6frac{4}{7} = 7cdot 6 + 4 = 46$ .
If the first four numbers are $20$ , and the last four numbers are $32$ , then all "eight" numbers are $20 + 32 = 52$ . But that's counting one number twice. Since the sum of all seven numbers is $46$ , then the number that was counted twice is $52 - 46 = 6$ , and the answer is $boxed{B}$

Algebraically, if $a + b + c + d = 20$ , and $d + e + f + g = 32$ , you can add both equations to get $a + b + c + 2d + e + f + g = 52$ . You know that $a + b + c + d + e + f + g = 46$ , so you can subtract that from the last equation to get $d = 6$ , and $d$ is the number that appeared twice.

Yay! 😀
As a strategy, think of how $angle B + angle D$ would be determined, particularly without determining either of the angles individually, since it may not be possible to determine $angle B$ or $angle D$ alone. If you see $triangle BFD$ , the you can see that the problem is solved quickly after determining $angle BFD$ .But start with $triangle AGF$ , since that's where most of our information is. Looking at $triangle AGF$ , since $angle F = angle G$ , and $angle A = 20$ , we can write: $angle A + angle G + angle F = 180$ $20 + 2angle F = 180$
$angle AFG = 80$

By noting that $angle AFG$ and $angle GFD$ make a straight line, we know

$angle AFG + angle GFD = 180$

$80 + angle GFD = 180$

$angle GFD = 100$

Ignoring all other parts of the figure and looking only at $triangle BFD$ , you see that $angle B + angle D + angle F = 180$ . But $angle F$ is the same as $angle GFD$ . Therefore:

$angle B + angle D + angle GFD = 180$ $angle B + angle D + 100 = 180$ $angle B + angle D = 80^circ$ , and the answer is thus $boxed{D}$
To quickly solve this multiple choice problem, make the (not necessarily valid, but very convenient) assumption that $ABCD$ can have any dimension. Give the rectangle dimensions of $AB = CD = 12$ and $BC = AD= 6$ , which is the easiest way to avoid fractions. Labelling the right midpoint as $M$ , and the bottom midpoint as $N$ , we know that $DN = NC = 6$ , and $BM = MC = 3$ . $[triangle ADN] = frac{1}{2}cdot 6cdot 6 = 18$ $[triangle MNC] = frac{1}{2}cdot 3cdot 6 = 9$ $[triangle ABM] = frac{1}{2}cdot 12cdot 3 = 18$
$[triangle AMN] = [square ABCD] - [triangle ADN] - [triangle MNC] - [triangle ABM]$

$[triangle AMN] = 72 - 18 - 9 - 18$

$[triangle AMN] = 27$ , and the answer is $boxed{B}$

The above answer is fast, but satisfying, and assumes that the area of $triangle AMN$ is independent of the dimensions of the rectangle. All in all, it's a very good answer though. However this is an alternative if you don't get the above answer. Label $AB = CD = l$ and $BC = DA = h$

Labelling $M$ and $N$ as the right and lower midpoints respectively, and redoing all the work above, we get:

$[triangle ADN] = frac{1}{2}cdot hcdot frac{l}{2} = frac{lh}{4}$

$[triangle MNC] = frac{1}{2}cdot frac{l}{2}cdot frac{w}{2} = frac{lh}{8}$

$[triangle ABM] = frac{1}{2}cdot lcdot frac{h}{2} = frac{lh}{4}$

$[triangle AMN] = [square ABCD] - [triangle ADN] - [triangle MNC] - [triangle ABM]$

$[triangle AMN] = lh - frac{lh}{4} - frac{lh}{8} - frac{lh}{4}$

$[triangle AMN] = frac{3}{8}lh = frac{3}{8}cdot 72 = 27$ , and the answer is $boxed{B}$