深度分析AMC8备战战略

AMC 是由美国数学协会于1950年在纽约创办的数学学术活动。创办之初参赛学生数便达到了6000人，现在每年更是有30万来自世界各地的学生慕名参与学术活动。作为美国数学奥林匹克学术活动国家队选拔的第一关，AMC按照初高中学生的年龄层次，依次分为AMC 8，AMC 10和AMC12，分别给初中、十年级和十二年级以下的学生参加。

AMC的设计初衷是为了鼓励初中学生锻炼解题和思考能力，因此考试题目更像趣味奥数题，很适合用来给孩子做课后练习。

AMC8学术活动规则和难度

AMC8一共25道选择题，每道题都是5选1的单选题，要在40分钟以内完成。每道题目做对可以得到1分，答错或不答0分。

AMC8它的前10题差不多相当于是小学到初中的学术活动题。然后11到20题差不多相当于从初中学术活动题逐渐过渡到一般的高中考试题，再过渡到联赛级别的普通题。然后21题到25题就逐渐从联赛普通题过渡到联赛大题的难度。

AMC8 考什么？

AMC8 的题目完美对应了大部分4-8年级学习的知识内容。从知识覆盖的角度来看，就算是单纯按照公立common core如此之慢的速度学起来，8年级已经覆盖98%的内容。光这四种题型，承包了几乎80%的题目比例。题目覆盖是一部分，难度又是另一部分。

根据MAA官网对于34年来题目的信息整合梳理后得出，最常出现的知识模块为

应用   （24%）

几何   （20%）

组合   （18%）

计算   （17%）

概率和统计    (12%）

数论    （9%）

AMC 8 的题有难有易。简单题一般1分钟内需要完成，难题才是攻克重点。针对总体上难度更大的21-25题的分析。

应用	13%
几何	31%
组合	26%
计算	6%
概率和统计	14%
数论	10%

难题数量顺序：几何>组合>统计>应用

几何、应用、组合不仅考的多、而且难题也多。

AMC8各个考点详细分析

AMC 8 考试最重要的一件事，是学会控制时间。40分钟完成25题，再加上检查的时间，平均一题只能花一分钟左右。

几何模块：

作为过去30多年占20%题量的模块，几何模块是无数考生备考中花费时间最多的。

很多AMC 8的几何题都是在几个模型的基础上进行变化，所以最重要的是熟练度、多总结。

几何模块：简单题

难度小的几何题不会涉及立体几何，而是简单的平面几何，考生往往可以通过目测就能够给出正确答案。

几何模块：难题

但是复杂的题目，如2013年第25题，考察了孩子的空间想象能力。想要做出这道题，一定要找出其中的陷阱。考生必须意识到小球的行走路径，并不是直接的三个半圆的周长相加。

计算模块：

在每年的卷子里都占有4-5题，一般不难。想要攻破这个模块，就是多多练习. 当然，计算也会有部分难题，主要考察的是巧算。

第一：背乘法口诀表。

第二：熟练掌握积累整数／分数／小数的加减乘除法的巧算。

应用题模块：

因为应用题考查的是从实际生活抽象出数学模型的能力，所以很多题目在数学维度是属于其他几个模块的。

应用题模块：简单题

简单的应用题，在理解题意上不会给孩子设置困难，学生往往能够很自然的从自己掌握的知识中找到能够解决这个实际问题对应的数学方法。

应用题模块：难题

有难度的应用题则需要孩子完全理解题目后搭建出一个数学模型。

数论模块：

所谓数论，主要研究整数的性质。被誉为‘最纯’的数学领域”，最简单数论问题例如什么是奇数什么是偶数。数论在AMC 8中考察的难度不会很深题量也不会很多。数论模块以及接下来要说的组合模块，有非常多的题并不在学校的学习范围内。

数论模块：简单题

简单的题，如2014年第4题，只要知道奇数必为一个偶数与一个奇数相加而得，而偶数的奇数只有2，就能很快求出答案 。

数论模块：难题

难度较大的题，如2018年第25题，则要求学生掌握指数运算的种种基本法则（初中才会学），对于想要跨级考AMC的低年级学生来说，难度非常的大。 而更难的题，不仅仅需要明确质数是什么，更是要了解唯一分解定理，如何通过质因子求解任意整数因数的个数。

但正如刚刚所言，数论再难也不会过分，因此在备考时，主要在准备因数与倍数，质数与合数的部分，多做题，多熟悉，很多题目就手到擒来。

组合模块：

组合模块也是校内涉及较少知识点而AMC考查较多的部分（难题中25%是组合模块的题）。组合涉及的考点非常多也非常杂，想要系统的准备是很有挑战性的，但是根据历年的真题，可以发现组合中的的逻辑推理，乘法原理，加法原理，复杂的计数都是难点与重点。

概统模块：难题

难度高的概统题常常为古典概型题，它的特点是可列有穷的，可以通过计数求出分子分母，因此难点主要在如何计数上。考题会与组合模块的内容高度结合，将计数过程变得非常复杂，学生首先需要理解事件发生的情况有哪几种可能性，然后不重不漏，又很高效地求出概率。

【总结】

·     AMC 8考试主要考察几何，计数，应用，数论，组合以及概统6个模块的内容。其中应用题在整张卷子里占比最多，几何在难题中占比最多。

·     组合与数论模块涉及的课外内容最多。

·     几何模块主要考察平面几何，可以在平时多积累各种模型与解题技巧。

·     计数模块鼓励大家学习乘法口诀表以及各种巧算的方法。

·     应用题在数学维度包含其他所有模块的知识，但考查的是孩子将实际问题转化为数学模型的能力。

·     数论占比虽然少，但难度较大，多积累因数与倍数，质数与合数的知识。

·     组合与概统模块都容易出现难题，需要靠多做题来提高题感以及解题策略。

学术活动报名扫码了解！免费领取历年真题！

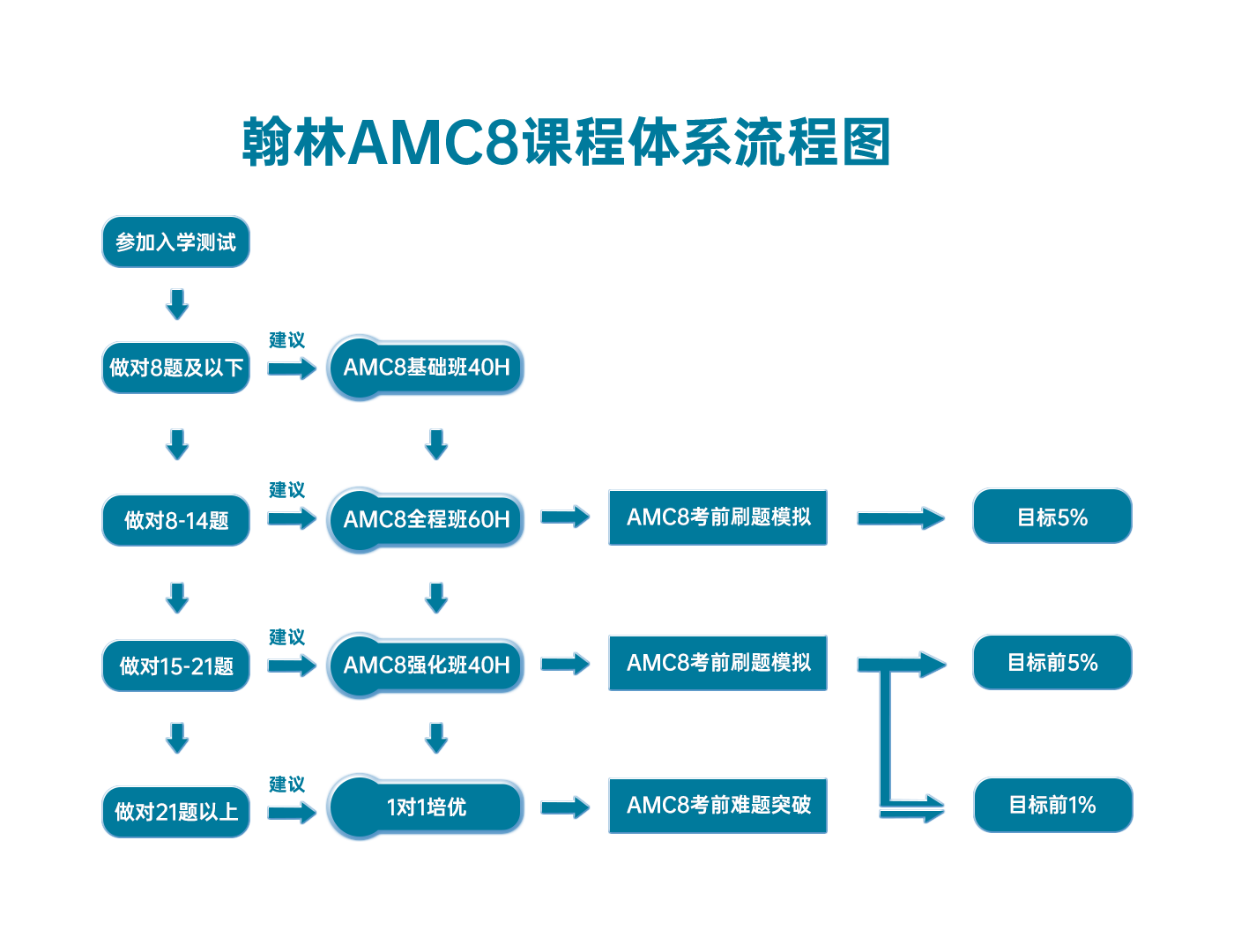
翰林AMC8课程体系流程图