数学建模竞赛全剖析

什么是数学模型和数学建模？

数学模型：

对于一个现实对象，为了一个特定目的，根据其内在

规律，作出必要的简化假设，运用适当的数学工具，

得到的一个数学结构。

数学建模：

建立数学模型的全过程

（包括表述、求解、解释、检验等）

数学建模的重要意义：

数学以空前的广度和深度向一切领域渗透。

在一般工程技术领域数学建模大有用武之地。

在高新技术领域数学建模几乎是必不可少的工具。

中国大学生数学建模学术活动（CUMCM）

中国大学生数学建模学术活动是全国高校规模最大的课外科技活动之一。该学术活动每年9月(一般在中旬某个周末的星期五至下周星期一共3天，72小时）举行，学术活动面向全国大专院校的学生，不分专业（但学术活动分本科、专科两组，本科组学术活动所有大学生均可参加，专科组学术活动只有专科生（包括高职、高专生）可以参加）。

美国大学生数学建模学术活动（MCM）

美国大学生数学建模学术活动（MCM/ICM），是一项国际级的学术活动项目，为现今各类数学建模学术活动之鼻祖。

MCM/ICM 是 Mathematical Contest in Modeling 和 Interdisciplinary Contest in Modeling 的缩写，即“数学建模学术活动”和“交叉学科建模学术活动”。MCM 始于 1985 年，ICM 始于 2000 年，由 COMAP（the Consortium for Mathematics and Its Application，美国数学及其应用联合会）主办，得到了 SIAM，NSA，INFORMS 等多个组织的赞助。MCM/ICM 着重强调研究问题、解决方案的原创性、团队合作、交流以及结果的合理性。

学术活动以三人（本科生）为一组，在四天时间内，就指定的问题完成从建立模型、求解、验证到论文撰写的全部工作。学术活动每年都吸引大量著名高校参赛。2008 年 MCM/ICM 有超过 2000 个队伍参加，遍及五大洲。MCM/ICM 已经成为最著名的国际大学生学术活动之一。

数学建模具体过程

 

 

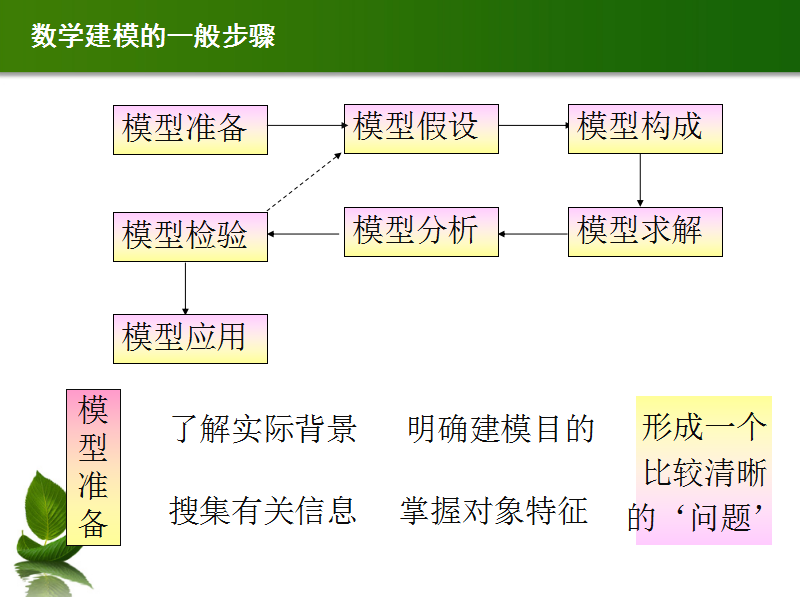
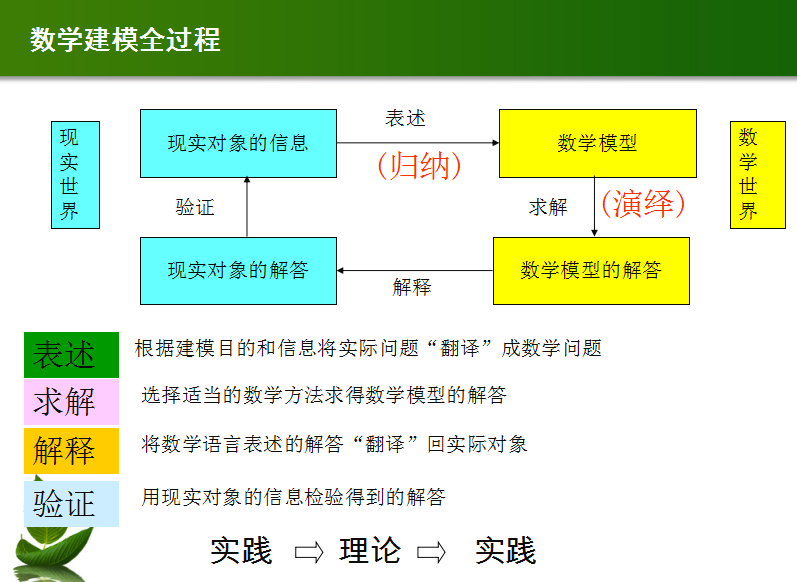
数据分析法

从大量的观测数据利用统计方法建立数学模型。

1. 回归分析法--用于对函数f（x）的一组观测值（xi, fi）i=1,2… n，确定函数的表达式，由于处理的是静态的独立数据，故称为数理统计方法。

2. 时序分析法--处理的是动态的相关数据，又称为过程统计方法。

仿真和其他方法

1. 计算机仿真（模拟）--实质上是统计估计方法，等效于抽样试验

① 离散系统仿真--有一组状态变量。

② 连续系统仿真--有解析表达式或系统结构图。

2. 因子试验法--在系统上作局部试验，再根据试验结果进行不断分析修改，求得所需的模型结构。

3. 人工现实法--基于对系统过去行为的了解和对未来希望达到的目标，并考虑到系统有关因素的可能变化，人为地组成一个系统。

学术活动技巧

三个人侧重点不同:

建模：推导数学模型，数学能力强

编程：计算机能力强

论文写作：写作能力强

学术活动时间安排

第一天：

上午：确定题目，并查阅文献

下午：开始分析，建立初步模型

晚上：编程，得到初步计算结果

12：00 PM 休息

第二天：

上午：得到第一个模型的合理结果

下午：开始写论文，并考虑对第一个模型的改进

第二天：

晚上：得到第二个模型的初步结果

12：00 PM 休息

第三天：

上午：得到第二个模型的合理结果

下午：考虑对前二个模型的进一步优化，得到第三个数学模型，或对前二个模型的正确性进行验证

晚上：得到最后结果，完成整篇论文

论文的重要性

1. 评定参赛队的成绩好坏、高低，获奖级别， 数模论文是唯一依据.

2. 论文是学术活动活动的成绩结晶的书面形式。

3.  写好论文的训练，是科技写作的一种基本训练。

论文格式规范

甲组参赛队从A、B题中任选一题，乙组参赛队从C、D题中任选一题。 论文用白色A4纸单面打印；上下左右各留出至少2.5厘米的页边距；从左侧装订。

论文第一页为承诺书，具体内容和格式见本规范第二页。 论文第二页为编号专用页，用于赛区和全国评阅前后对论文进行编号，具体内容和格式见本规范第三页。

论文题目和摘要写在论文第三页上，从第四页开始是论文正文。 论文从第三页开始编写页码，页码必须位于每页页脚中部，用阿拉伯数字从“1”开始连续编号。

论文不能有页眉，论文中不能有任何可能显示答题人身份的标志。 论文题目用三号黑体字、一级标题用四号黑体字，并居中。

论文中其他汉字一律采用小四号宋体字，行距用单倍行距，打印时应尽量避免彩色打印。

提请大家注意：摘要应该是一份简明扼要的详细摘要（包括关键词），在整篇论文评阅中占有重要权重，请认真书写（注意篇幅不能超过一页，且无需译成英文）。

引用别人的成果或其他公开的资料（包括网上查到的资料）必须按照规定的参考文献的表述方式在正文引用处和参考文献中均明确列出。正文引用处用“[]”标出，如[1][3]等。

参考文献按正文中的引用次序列出，其中

书籍的表述方式为：

[编号] 作者，书名，出版地：出版社，出版年

期刊杂志论文的表述方式为：

[编号] 作者，论文名，杂志名，卷期号：起止页码，出版年

网上资源的表述方式为：

[编号] 作者，资源标题，网址，访问时间（年月日）

论文结构

1、摘要

2、问题的叙述，问题的分析，背景的分析等，

3、模型的假设，符号说明（表）

4、模型的建立（问题分析，公式推导，基本模型， 最终或简化模型 等

5、模型的求解

6、模型检验:结果表示、分析与检验，误差分析，……

7、模型评价:特点，优缺点，改进方法，推广…….

8、参考文献

9、 附录：计算框图、详细图表……

论文写作之问题重述

不能简单的照抄题目！

将原问题用数学的语言表达出来

重点解决的问题应着重说明，把阅卷老师引导到自己的思路中，把他们看成不懂本问题的读者。

论文写作之模型假设及符号说明

最关键的一步从假设开始。需要下很大功夫，简明扼要、准确清楚

1）假设太多，阅卷老师记不住。要归结出一些重要的假设，一般3~5条，有些不是很重要的假设在论文适当的地方提一下

2）假设要数学化，重视逻辑性要求

3）设计好符号，使人看起来清楚（简洁、通用）

论文写作之模型建立

（1）基本模型

1) 首先要有数学模型：数学公式、方案等

2) 基本模型，要求 完整，正确，简明

（2）简化模型

1）要明确说明：简化思想，依据

2）简化后模型，尽可能完整给出

（3）模型要实用，有效，以解决问题有效为原则。数学建模面临的、要解决的是实际问题，不追求数学上的高（级）、深（刻）、难（度大）。

（4）鼓励创新，但要切实，不要离题搞标新立异,数模创新可出现在

▲建模中，模型本身，简化的好方法、好策略等，

▲模型求解中

▲结果表示、分析，模型检验

▲推广部分

(5)在问题分析推导过程中，需要注意的问题

分析：中肯、确切；

术语：专业、内行；

原理、依据：正确、明确；

表述：简明，关键步骤要列出；

忌：外行话，专业术语不明确，表述混乱、繁琐。

能用初等方法解决的、就不用高级方法；

能用简单方法解决的，就不用复杂方法；

能用被更多人看懂、理解的方法，就不用只能少数人看懂、理解的方法。

论文写作之模型的求解

（1）需要建立数学命题时：命题叙述要符合数学命题的表述规范，尽可能论证严密；

（2）需要说明计算方法或算法的原理、思想、依据、步骤。若采用现有软件，说明采用此软件的理由，软件名称；

（3）计算过程，中间结果可要可不要的，不要列出。

（4）设法算出合理的数值结果。

论文写作之模型检验和结果分析

（1）最终数值结果的正确性或合理性是第一位的 ；

（2）对数值结果或模拟结果进行必要的检验。结      果不正确、不合理、或误差大时，分析原因，对算法、计算方法、或模型进行修正、改进；

（3）题目中要求回答的问题，数值结果，结论，须一一列出；

（4）结果表示：要集中，一目了然，直观，便于比较分析

▲数值结果表示：精心设计表格；可能的话，用图形图表形式

模型评价

优点突出，缺点不回避。改变原题要求，重新建模可在此做。推广或改进方向时，不要玩弄新数学术语。