2009 USAMO Problems真题及答案

2009 USAMO Problems真题及答案

完整版真题免费下载

+答案解析请参考文末

真题下载请前往【纯真题】小程序

Day 1

Problem 1

Given circles  and  intersecting at points  and , let  be a line through the center of  intersecting  at points  and  and let  be a line through the center of  intersecting  at points  and . Prove that if  and  lie on a circle then the center of this circle lies on line .

Problem 2

Let  be a positive integer. Determine the size of the largest subset of  which does not contain three elements  (not necessarily distinct) satisfying .

Problem 3

We define a chessboard polygon to be a polygon whose sides are situated along lines of the form  or , where  and  are integers. These lines divide the interior into unit squares, which are shaded alternately grey and white so that adjacent squares have different colors. To tile a chessboard polygon by dominoes is to exactly cover the polygon by non-overlapping  rectangles. Finally, a tasteful tiling is one which avoids the two configurations of dominoes shown on the left below. Two tilings of a  rectangle are shown; the first one is tasteful, while the second is not, due to the vertical dominoes in the upper right corner.

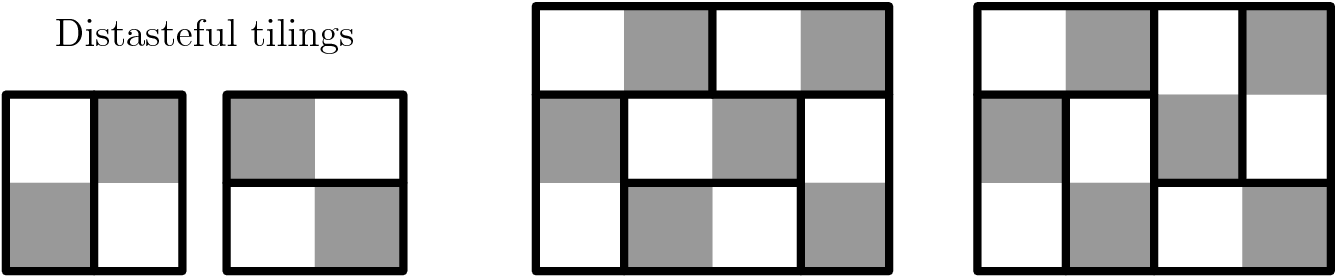
a) Prove that if a chessboard polygon can be tiled by dominoes, then it can be done so tastefully.

b) Prove that such a tasteful tiling is unique.

Day 2

Problem 4

For  let , , ...,  be positive real numbers such that

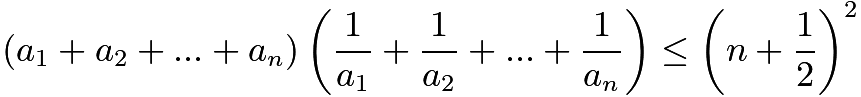Prove that .

Problem 5

Trapezoid , with , is inscribed in circle  and point  lies inside triangle . Rays  and  meet  again at points and , respectively. Let the line through  parallel to  intersect  and  at points  and , respectively. Prove that quadrilateral  is cyclic if and only if  bisects .

Problem 6

Let  be an infinite, nonconstant sequence of rational numbers, meaning it is not the case that  Suppose that  is also an infinite, nonconstant sequence of rational numbers with the property that  is an integer for all  and . Prove that there exists a rational number  such that  and  are integers for all  and .

[wechat keyword="usamo" key="usamohanlin"]

Problem 1

Solution

Let  be the circumcircle of ,  to be the radius of , and  to be the center of the circle , where . Note that  and  are the radical axises of  ,  and  ,  respectively. Hence, by power of a point(the power of  can be expressed using circle  and  and the power of  can be expressed using circle  and ),Subtracting these two equations yields that , so  must lie on the radical axis of  , .

~AopsUser101

Remarks

Conveniently, this analytic solution takes care of all configuration issues we may have encountered had we used a more traditional solution, such as angle-chasing(which would indeed work, just be considerably less elegant).

~AopsUser101

Problem 2

Solution 1

Let  be a subset of  of largest size satisfying  for all . First, observe that . Next note that , by observing that the set of all the odd numbers in  works. To prove that , it suffices to only consider even , because the statement for  implies the statement for  as well. So from here forth, assume  is even.

For any two sets  and , denote by  the set , and by  the set . Also, let  denote  and  denote . First, we present a lemma:

Lemma 1: Let  and  be two sets of integers. Then .

Proof: Write  and  where  and . Then  is a strictly increasing sequence of  integers in .

Now, we consider two cases:

Case 1: One of  is not in . Without loss of generality, suppose . Let  (a set with  elements), so that  by our assumption. Now, the condition that  for all  implies that . Since any element of  has absolute value at most , we have . It follows that , so . However, by Lemma 1, we also have . Therefore, we must have , or , or .

Case 2: Both  and  are in . Then  and  are not in , and at most one of each of the pairs 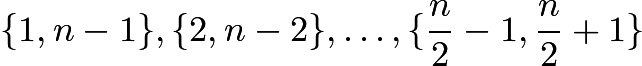 and their negatives are in . This means  contains at most  elements.

Thus we have proved that  for even , and we are done.

Solution 2

Let  be the set of subsets satisfying the  condition for , and let  be the largest size of a set in . Let  if  is even, and  if  is odd. We note that  due to the following constuction:or all of the odd numbers in the set. Then the sum of any three will be odd and thus nonzero.

Lemma 1: . If , then we note that , so . 

Lemma 2: . Suppose, for sake of contradiction, that  and . Remove  from , and partition the rest of the elements into two sets , where  and  contain all of the positive and negative elements of , respectively. (obviously , because ). WLOG, suppose . Then . We now show the following two sub-results:

Sub-lemma (A): if ,  [and similar for ]; andSub-lemma (B): we cannot have both  and  simultaneously hold.

This is sufficient, because the only two elements that may be in  that are not in  are  and ; for , we must either have  and both  [but by pigeonhole , see sub-lemma (A)], or , and , in which case by (A) we must have , violating (B).

(A): Partition  into the  sets . Because , then if any of those sets are within , . But by Pigeonhole at most  elements may be in , contradiction.

(B): We prove this statement with another induction. We see that the statement easily holds true for  or , so suppose it is true for , but [for sake of contradiction] false for . Let , and similarly for . Again WLOG . Then we have .

If , then by inductive hypothesis, we must have . But (A) implies that we cannot add  or . So to satisfy  we must have  added, but then  contradiction.

If , then at least three of  added. But , and by (A) we have that  cannot be added. If , then another grouping similar to (A) shows that  canno be added, contradiction. So , , and adding the three remaining elements gives contradiction.

If , then all four of  must be added, and furthermore . Then , and by previous paragraph we cannot add . 

So we have 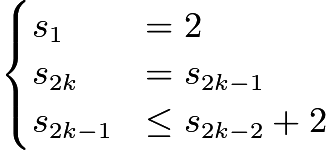 and by induction, that 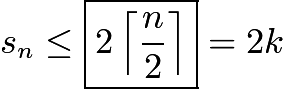, which we showed is achievable above.

Problem 3

暂无官方Solutions，可联系翰林导师进行详解。欢迎点击联系我们资讯翰林顾问！

Problem 4

Solution

Assume without loss of generality that . Now we seek to prove that .

By the Cauchy-Schwarz Inequality,Since , clearly 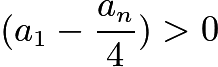, dividing yields:

as desired.

Problem 5

Solution 1

We will use directed angles in this solution. Extend  to  as follows:

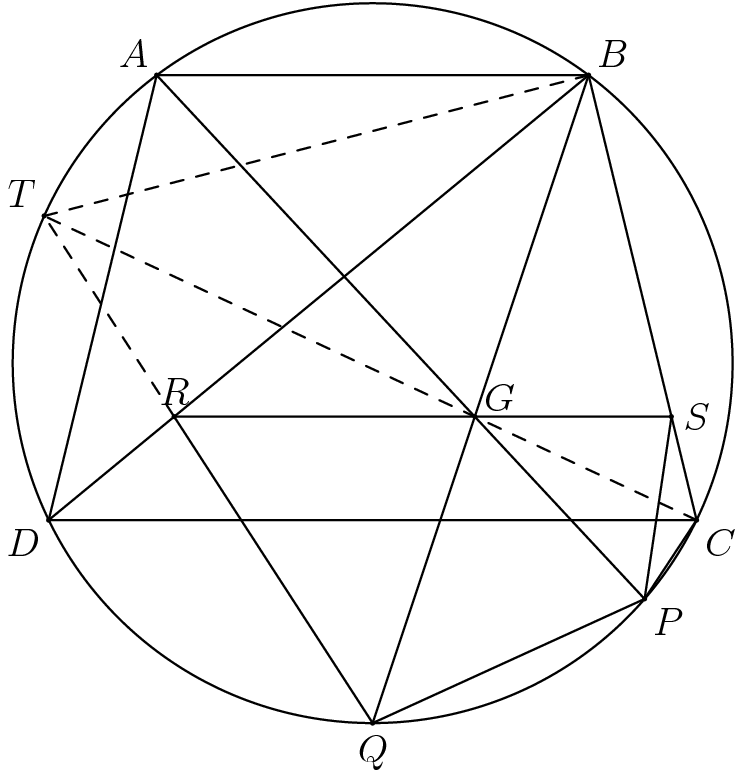If:

Note that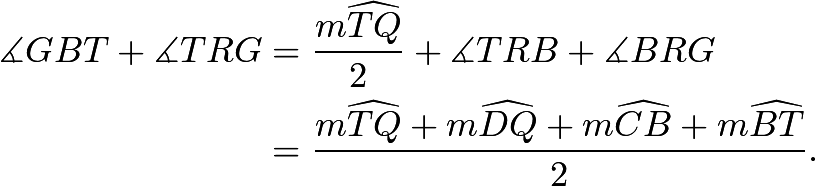Thus,  is cyclic.

Also, note that  is cyclic because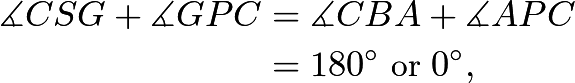depending on the configuration.

Next, we have  are collinear since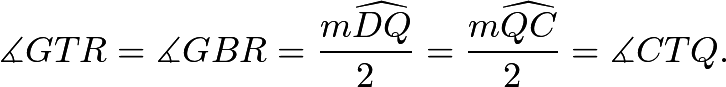

Therefore,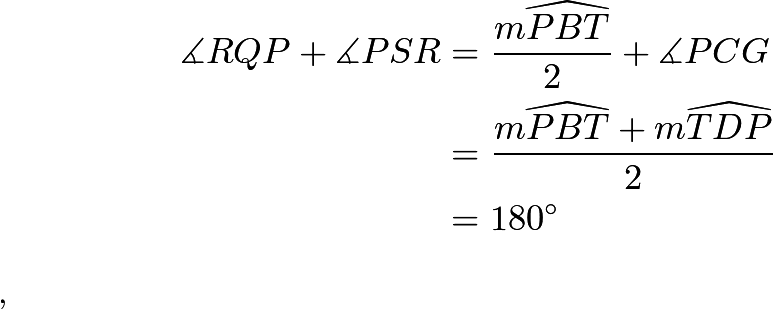so  is cyclic.

Only If: These steps can be reversed.

Solution 2 (Projective)

Extend  to , and let line  intersect  at  and another point , as shown:

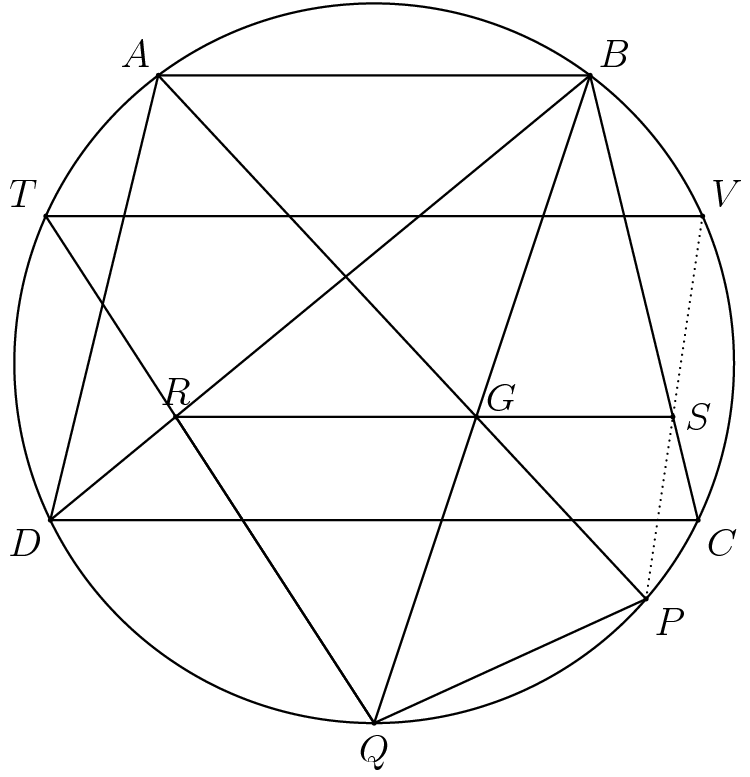
If:

Suppose that , and . Pascal's theorem on the tuple  implies that the points , , and  are collinear. However,  and  are symmetrical with respect to the axis of symmetry of trapezoid , and  and  are also symmetrical with respect to the axis of symmetry of  (as  is the midpoint of , and ). Since ,  and  are symmetric with respect to the axis of symmetry of trapezoid . This implies that line  is equivalent to line . Thus,  lies on line . However, , so this implies that .

Now note that  is cyclic. Since , . However, . Therefore,  is cyclic.

Only If:

Consider the same setup, except  is no longer the midpoint of . Note that  must be parallel to  in order for  to be cyclic. We claim that  and hope to reach a contradiction. Pascal's theorem on the tuple  implies that , , and  are collinear. However, there exists a unique point  such that , , and  are concurrent. By If,  must be the midpoint of  in order for the concurrency to occur; hence, . Then , since . However, this is a contradiction, so therefore  cannot be parallel to  and  is not cyclic.

Solution by TheBoomBox77

Problem 6

暂无官方Solutions，可联系翰林导师进行详解。欢迎点击联系我们资讯翰林顾问！