2012 USAMO Problems真题及答案

2012 USAMO Problems真题及答案

完整版真题免费下载

+答案解析请参考文末

Day 1

Problem 1

Find all integers  such that among any  positive real numbers , , ,  withthere exist three that are the side lengths of an acute triangle.

Problem 2

A circle is divided into 432 congruent arcs by 432 points. The points are colored in four colors such that some 108 points are colored Red, some 108 points are colored Green, some 108 points are colored Blue, and the remaining 108 points are colored Yellow. Prove that one can choose three points of each color in such a way that the four triangles formed by the chosen points of the same color are congruent.

Problem 3

Determine which integers  have the property that there exists an infinite sequence , , ,  of nonzero integers such that the equalityholds for every positive integer .

Day 2

Problem 4

Find all functions  (where  is the set of positive integers) such that  for all positive integers  and such that  divides  for all distinct positive integers , .

Problem 5

Let  be a point in the plane of triangle , and  a line passing through . Let , ,  be the points where the reflections of lines , ,  with respect to  intersect lines , , , respectively. Prove that , ,  are collinear.

Problem 6

For integer , let , , ,  be real numbers satisfyingFor each subset , define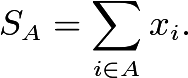(If  is the empty set, then .)

Prove that for any positive number , the number of sets  satisfying  is at most . For what choices of , , , ,  does equality hold?