Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2015 USAJMO Problems真题及答案

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年8月13日上午11:41

2015 USAJMO Problems真题及答案

完整版真题免费下载

+答案解析请参考文末

Day 1

Problem 1

Given a sequence of real numbers, a move consists of choosing two terms and replacing each with their arithmetic mean. Show that there exists a sequence of 2015 distinct real numbers such that after one initial move is applied to the sequence -- no matter what move -- there is always a way to continue with a finite sequence of moves so as to obtain in the end a constant sequence.

Problem 2

Solve in integers the equation $[x^2+xy+y^2 = left(frac{x+y}{3}+1right)^3.]$

Problem 3

Quadrilateral $APBQ$ is inscribed in circle $omega$ with $angle P = angle Q = 90^{circ}$ and $AP = AQ < BP$ . Let $X$ be a variable point on segment $overline{PQ}$ . Line $AX$ meets $omega$ again at $S$ (other than $A$ ). Point $T$ lies on arc $AQB$ of $omega$ such that $overline{XT}$ is perpendicular to $overline{AX}$ . Let $M$ denote the midpoint of chord $overline{ST}$ . As $X$ varies on segment $overline{PQ}$ , show that $M$ moves along a circle.

Day 2

Problem 4

Find all functions $f:mathbb{Q}rightarrowmathbb{Q}$ such that $[f(x)+f(t)=f(y)+f(z)]$ for all rational numbers $x<y<z<t$ that form an arithmetic progression. ( $mathbb{Q}$ is the set of all rational numbers.)

Problem 5

Let $ABCD$ be a cyclic quadrilateral. Prove that there exists a point $X$ on segment $overline{BD}$ such that $angle BAC=angle XAD$ and $angle BCA=angle XCD$ if and only if there exists a point $Y$ on segment $overline{AC}$ such that $angle CBD=angle YBA$ and $angle CDB=angle YDA$ .

Problem 6

Steve is piling $mgeq 1$ indistinguishable stones on the squares of an $ntimes n$ grid. Each square can have an arbitrarily high pile of stones. After he finished piling his stones in some manner, he can then perform stone moves, defined as follows. Consider any four grid squares, which are corners of a rectangle, i.e. in positions $(i, k), (i, l), (j, k), (j, l)$ for some $1leq i, j, k, lleq n$ , such that $i<j$ and $k<l$ . A stone move consists of either removing one stone from each of $(i, k)$ and $(j, l)$ and moving them to $(i, l)$ and $(j, k)$ respectively, or removing one stone from each of $(i, l)$ and $(j, k)$ and moving them to $(i, k)$ and $(j, l)$ respectively.

Two ways of piling the stones are equivalent if they can be obtained from one another by a sequence of stone moves.

How many different non-equivalent ways can Steve pile the stones on the grid?

2015USAJMO真题参考答案及详解

Problem 1

Solution

Let the set be ${-1007, -1006, ...0,1,2...1006, 1007}$ , namely all the consecutive integers from $-1007$ to $1007$ . Notice that the operation we are applying in this problem does not change the sum or the mean of the set, which is $0$ .

There are $1007$ pairs of opposite integers ${a,-a}$ . After the first two elements are chosen, there are at least $1005$ such pairs. For each such pair we perform the operation of average, hence reducing these $2010$ elements to $0$ . Then use the other $5$ elements together with three $0$ 's produced to form the group of eight: ${a_1,a_2,a_3,a_4,a_5,a_6=0,a_7=0,a_8=0}$ , and perform the operation in the following order: $[(a_1,a_2)to(m_1,m_1), (a_3,a_4)to(m_2,m_2), (a_5,a_6)to(m_3,m_3), (a_7,a_8)to(m_4,m_4),]$ where $m_i=frac{a_i+a_{i+1}}{2}$ . Then, $(m_1,m_2)to(m_{11}, m_{11})$ for two groups, $(m_3,m_4)to(m_{12}, m_{12})$ for the other two groups, and finally $(m_{11},m_{12})to(m_{111}, m_{111})$ for all the eight elements. Since the sum of the eight-group is $0$ , $m_{111}$ must also be $0$ . Therefore, all the elements are reduced to $0$ .

The key to the algorithm is to form a $2^k$ subset, which is guaranteed to be reducible to all the members of the same value, namely the mean. Then before that, if we could always choose $Mge N-2^k$ members to form pairs, each yielding the average of the total group, then all the members are reduced to the average. Under the condition that two arbitrary elements are chosen first, we need only $Nge4$ to guarantee this result. But for $N=2$ the first operation leads to equal elements, so $N=3$ is the only case when all the members may not be reduced to average.

Sidenote: Actually, for $N=3$ , the members are all reduced to the average, as the sum of the terms is constant and does not change.

Solution 2 (INCORRECT)

Let the set be ${a_1,a_2,dots ,a_{2015}}$ , where all the terms are nonnegative. Note that the sum of all the terms in this sequence will always be the same after any amount of moves. To prove this, let $i,j$ be integers with $1le i<jle 2015$ , and we have $a_i+a_j = frac{a_i+a_j}{2}+frac{a_i+a_j}{2}$ .

Also, $a_ia_j le (frac{a_i+a_j}{2})(frac{a_i+a_j}{2})$ by AM-GM, so the product of all the terms will not decrease after any number of moves. However, the product will only stay the same when $a_i=a_j$ , so the product will always increase if $a_ine a_j$ .

Finally, note that $a_1a_2dots a_{2015}le (frac{a_1+a_2+dots +a_{2015}}{2015})^{2015}$ by AM-GM, so because $a_1+a_2+dots +a_{2015}$ is fixed, there is a maximum product that is reached after a finite number of moves as the product increases. This product is reached when $a_1=a_2=dots =a_{2015}$ , so we are done.

This solution is incorrect; the product may take an infinite number of moves to reach the maximum (for example, consider the sequence $1, 3, 4, 5... 2016$ )

Problem 2

Solution

We first notice that both sides must be integers, so $frac{x+y}{3}$ must be an integer.

We can therefore perform the substitution $x+y = 3t$ where $t$ is an integer.

Then:

$begin{align*} (3t)^2 - xy &= (t+1)^3 \ 9t^2 + x (x - 3t) &= t^3 + 3t^2 + 3t + 1 \ 4x^2 - 12xt + 9t^2 &= 4t^3 - 15t^2 + 12t + 4 \ (2x - 3t)^2 &= (t - 2)^2(4t + 1) end{align*}$

$4t+1$ is therefore the square of an odd integer and can be replaced with $(2n+1)^2 = 4n^2 + 4n +1$ .

By substituting using $t = n^2 + n$ we get:

$begin{align*} (2x - 3n^2 - 3n)^2 &= [(n^2 + n - 2)(2n+1)]^2 \ 2x - 3n^2 - 3n &= pm (2n^3 + 3n^2 -3n -2) \ x = n^3 + 3n^2 - 1 &text{ or } x = - n^3 + 3n + 1 end{align*}$

Using substitution we get the solutions: $(n^3 + 3n^2 - 1, - n^3 + 3n + 1) cup ( - n^3 + 3n + 1, n^3 + 3n^2 - 1)$

Problem 3

Solution 1

$[asy] size(8cm); pair A=(1,0); pair B=(-1,0); pair P=dir(70); pair Q=dir(-70); pair O=(0,0); pair X=0.3*P + 0.7*Q; pair Y=5*X-4*A; pair S=intersectionpoints(A--Y,circle(O,1))[1]; pair Z=(A-X)*dir(-90) + X; pair T=intersectionpoint(X--Z,circle(O,1)); pair M=(S+T)/2; draw(circle(O,1)); draw(B--A--P--B--Q--A--S--T--X); draw(P--Q); dot("$A$",A,dir(A)); dot("$B$",B,dir(B)); dot("$P$",P,dir(P)); dot("$Q$",Q,dir(Q)); dot("$X$", X, SE); dot("$S$",S,dir(S)); dot("$T$",T,dir(T)); dot("$M$",M,dir(M)); dot((0,0)); [/asy]$

We will use coordinate geometry.

Without loss of generality, let the circle be the unit circle centered at the origin, $[A=(1,0) P=(1-a,b), Q=(1-a,-b)]$ , where $(1-a)^2+b^2=1$ .

Let angle $angle XAB=A$ , which is an acute angle, $tan{A}=t$ , then $X=(1-a,at)$ .

Angle $angle BOS=2A$ , $S=(-cos(2A),sin(2A))$ . Let $M=(u,v)$ , then $T=(2u+cos(2A), 2v-sin(2A))$ .

The condition $TX perp AX$ yields: $(2v-sin(2A)-at)/(2u+cos(2A)+a-1)=cot A.$ (E1)

Use identities $(cos A)^2=1/(1+t^2)$ , $cos(2A)=2(cos A)^2-1= 2/(1+t^2) -1$ , $sin(2A)=2sin Acos A=2t^2/(1+t^2)$ , we obtain $2vt-at^2=2u+a$ . (E1')

The condition that $T$ is on the circle yields $(2u+cos(2A))^2+ (2v-sin(2A))^2=1$ , namely $vsin(2A)-ucos(2A)=u^2+v^2$ . (E2)

$M$ is the mid-point on the hypotenuse of triangle $STX$ , hence $MS=MX$ , yielding $(u+cos(2A))^2+(v-sin(2A))^2=(u+a-1)^2+(v-at)^2$ . (E3)

Expand (E3), using (E2) to replace $2(vsin(2A)-ucos(2A))$ with $2(u^2+v^2)$ , and using (E1') to replace $a(-2vt+at^2)$ with $-a(2u+a)$ , and we obtain $u^2-u-a+v^2=0$ , namely $(u-frac{1}{2})^2+v^2=a+frac{1}{4}$ , which is a circle centered at $(frac{1}{2},0)$ with radius $r=sqrt{a+frac{1}{4}}$ .

Solution 2

Let the midpoint of $AO$ be $K$ . We claim that $M$ moves along a circle with radius $KP$ .

We will show that $KM^2 = KP^2$ , which implies that $KM = KP$ , and as $KP$ is fixed, this implies the claim.

$KM^2 = frac{AM^2+OM^2}{2}-frac{AO^2}{4}$ by the median formula on $triangle AMO$ .

$KP^2 = frac{AP^2+OP^2}{2}-frac{AO^2}{4}$ by the median formula on $triangle APO$ .

$KM^2-KP^2 = frac{1}{2}(AM^2+OM^2-AP^2-OP^2)$ .

As $OP = OT$ , $OP^2-OM^2 = MT^2$ from right triangle $OMT$ . $(1)$

By $(1)$ , $KM^2-KP^2 = frac{1}{2}(AM^2-MT^2-AP^2)$ .

Since $M$ is the circumcenter of $triangle XTS$ , and $MT$ is the circumradius, the expression $AM^2-MT^2$ is the power of point $A$ with respect to $(XTS)$ . However, as $AX*AS$ is also the power of point $A$ with respect to $(XTS)$ , this implies that $AM^2-MT^2=AX*AS$ . $(2)$

By $(2)$ , $KM^2-KP^2 = frac{1}{2}(AX*AS-AP^2)$

Finally, $triangle APX sim triangle ASP$ by AA similarity ( $angle XAP = angle SAP$ and $angle APX = angle AQP = angle ASP$ ), so $AX*AS = AP^2$ . $(3)$

By $(3)$ , $KM^2-KP^2=0$ , so $KM^2=KP^2$ , as desired. $QED$

Problem 4

Solution

According to the given, $f(x-a)+f(x+0.5a)=f(x-0.5a)+f(x)$ , where x and a are rational. Likewise $f(x-0.5a)+f(x+a)=f(x+0.5a)+f(x)$ . Hence $f(x+a)-f(x)= f(x)-f(x-a)$ , namely $2f(x)=f(x-a)+f(x+a)$ . Let $f(0)=C$ , then consider $F(x)=f(x)-C$ , where $F(0)=0,$ $2F(x)=F(x-a)+F(x+a)$ .

$F(2x)=F(x)+[F(x)-F(0)]=2F(x)$ , $F(3x)=F(2x)+[F(2x)-F(x)]=3F(x)$ . Easily, by induction, $F(nx)=nF(x)$ for all integers $n$ . Therefore, for nonzero integer m, $(1/m)F(mx)=F(x)$ , namely $F(x/m)=(1/m)F(x)$ Hence $F(n/m)=(n/m)F(1)$ . Let $F(1)=k$ , we obtain $F(x)=kx$ , where $k$ is the slope of the linear functions, and $f(x)=kx+C$ .

Problem 5

Solution 1

Note that lines $AC, AX$ are isogonal in $triangle ABD$ , so an inversion centered at $A$ with power $r^2=ABcdot AD$ composed with a reflection about the angle bisector of $angle DAB$ swaps the pairs $(D,B)$ and $(C,X)$ . Thus, $[frac{AD}{XD}cdot frac{XD}{CD}=frac{AC}{BC}cdot frac{AB}{CA}Longrightarrow (A,C;B,D)=-1]$ so that $ACBD$ is a harmonic quadrilateral. By symmetry, if $Y$ exists, then $(B,D;A,C)=-1$ . We have shown the two conditions are equivalent, whence both directions follow $.:blacksquare:$

Solution 2

All angles are directed. Note that lines $AC, AX$ are isogonal in $triangle ABD$ and $CD, CE$ are isogonal in $triangle CDB$ . From the law of sines it follows that

$[frac{DX}{XB}cdot frac{DE}{ED}=left(frac{AD}{DB}right)^2=left(frac{DC}{BC}right)^2.]$

Therefore, the ratio equals $frac{ADcdot DC}{DBcdot BC}.$

Now let $Y$ be a point of $AC$ such that $angle{ABE}=angle{CBY}$ . We apply the above identities for $Y$ to get that $frac{CY}{YA}cdot frac{CE}{EA}=left(frac{CD}{DA}right)^2$ . So $angle{CDY}=angle{EDA}$ , the converse follows since all our steps are reversible.

Beware that directed angles, or angles $mod$ $180$ , are not standard olympiad material. If you use them, provide a definition.

Problem 6

Solution

Let the number of stones in row $i$ be $r_i$ and let the number of stones in column $i$ be $c_i$ . Since there are $m$ stones, we must have $sum_{i=1}^n r_i=sum_{i=1}^n c_i=m$

Lemma 1: If any $2$ pilings are equivalent, then $r_i$ and $c_i$ are the same in both pilings $forall i$ .

Proof: We suppose the contrary. Note that $r_i$ and $c_i$ remain invariant after each move, therefore, if any of the $r_i$ or $c_i$ are different, they will remain different.

Lemma 2: Any $2$ pilings with the same $r_i$ and $c_i$ $forall i$ are equivalent.

Proof: Suppose piling 1 and piling 2 not the same piling. Call a stone in piling 1 wrong if the stone occupies a position such that there are more stones in that position in piling 1 than piling 2. Similarly define a wrong stone in piling 2. Let a wrong stone be at $(a, b)$ in piling 1. Since $c_b$ is the same for both pilings, we must have a wrong stone in piling 2 at column b, say at $(c, b)$ , such that $cnot = a$ . Similarly, we must have a wrong stone in piling 1 at row c, say at $(c, d)$ where $d not = b$ . Clearly, making the move $(a,b);(c,d) implies (c,b);(a,d)$ in piling 1 decreases the number of wrong stones in piling 1. Therefore, the number of wrong stones in piling 1 must eventually be $0$ after a sequence of moves, so piling 1 and piling 2 are equivalent.

Lemma 3: Given the sequences $g_i$ and $h_i$ such that $sum_{i=1}^n g_i=sum_{i=1}^n h_i=m$ and $g_i, h_igeq 0 forall i$ , there is always a piling that satisfies $r_i=g_i$ and $c_i=h_i$ $forall i$ .

Proof: We take the lowest $i$ , $j$ , such that $g_i, h_j >0$ and place a stone at $(i, j)$ , then we subtract $g_i$ and $h_j$ by $1$ each, until $g_i$ and $h_i$ become $0$ $forall i$ , which will happen when $m$ stones are placed, because $sum_{i=1}^n g_i$ and $sum_{i=1}^n h_i$ are both initially $m$ and decrease by $1$ after each stone is placed. Note that in this process $r_i+g_i$ and $c_i+h_i$ remains invariant, thus, the final piling satisfies the conditions above.

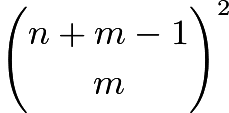By the above lemmas, the number of ways to pile is simply the number of ways to choose the sequences $r_i$ and $c_i$ such that $sum_{i=1}^n r_i=sum_{i=1}^n c_i=m$ and $r_i, c_i geq 0 forall i$ . By stars and bars, the number of ways is $binom{n+m-1}{m}^{2}$ .