从特例入手讨论AMC12试题

并不是所有学术活动试题的解答都要炫技

有时解题就像生活，要从特殊窥见一般

如何提高数学水平，有时需要小题大做

The 2006 American Mathematics Competition-12 (AMC-12) B exam included the following question：

An object in the plane moves from one lattice point to another. At each step, the object may move one unit up, down, left, or right. If the object starts at the origin and takes a 10-step path, how many different points can be the final point?

平面中的对象从一个格点移动到另一个格点。在每个步骤中，物体可以向上、向下、向左或向右移动一个单元。如果物体从原点开始，走10步的路径，那么最后一个点可以是多少个不同的点？

这是一个有趣的问题，通过研究它，你会对这里提出的解决方案产生兴趣。通过计算1、2和3步之后可以达到多少个点，然后会发现一个规律，从而找到答案。

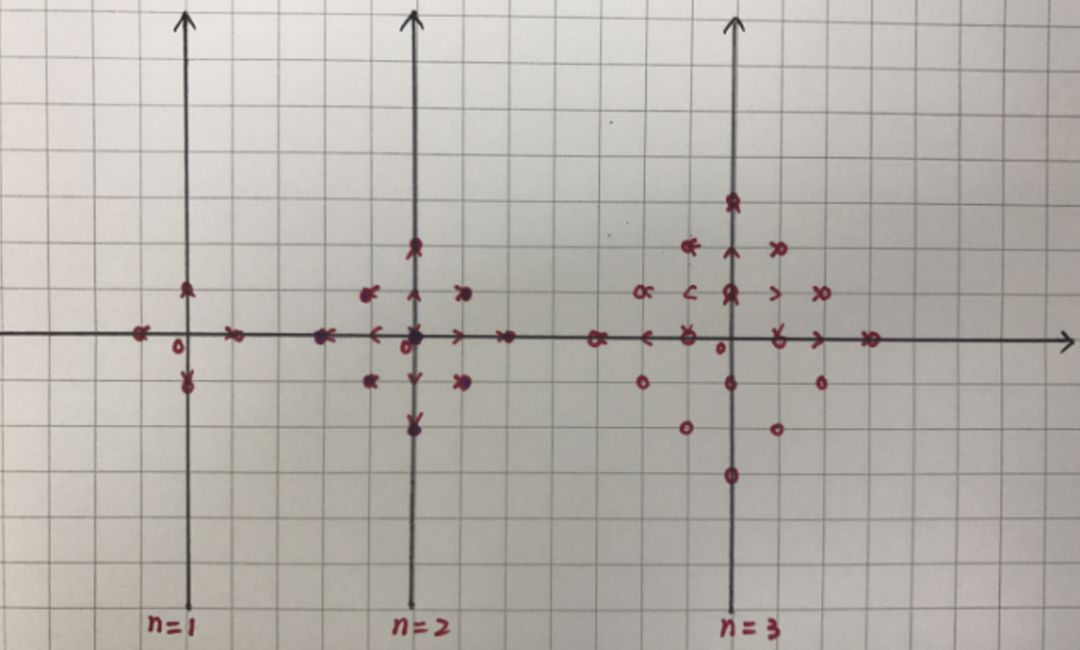
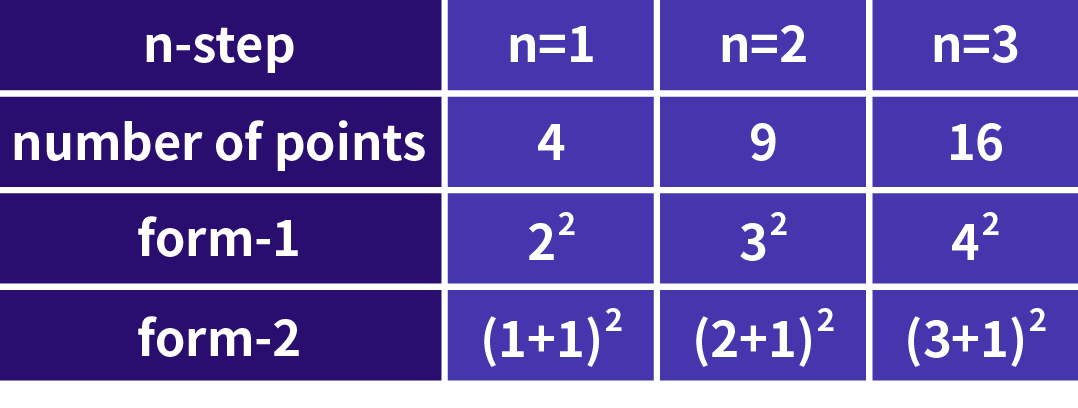
如果你的数字感觉强，你也会用上面这个表格给出的过程进行思考的找到规律的。经过n步，物体可以在(n+1)2个不同的格点，所以问题中要求10步，那么答案就是121。为了比赛的目的，从特例入手解决问题是一个常见的办法。

可以有人会说这不就是猜吗，太牵强了吧。那好，我们可以继续从特例入手，是否可以用到课本教材中常用的分析方法呢。点数的变化，从4开始，依次是9, 16, 25, 36...考虑点数之间的相互关系,用递推的方法也是可以得出最终的规律。这个方法，我们在学习数列，等差数列时经常用到。

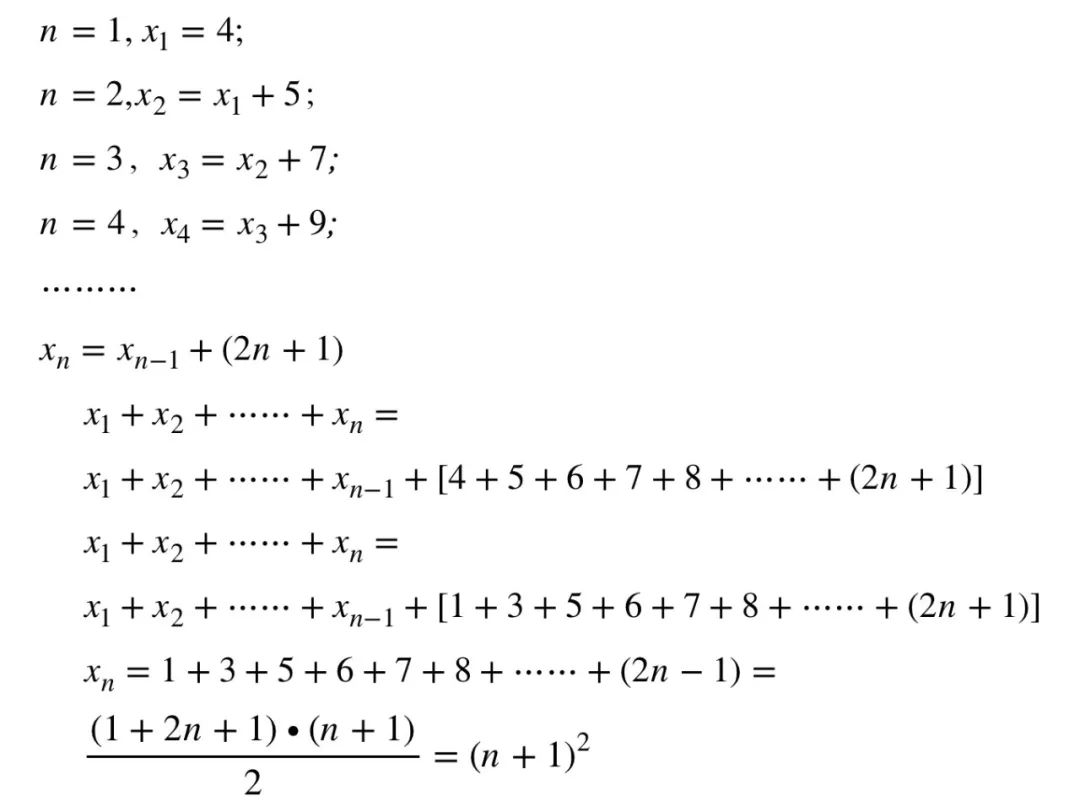
但是上述两个方法都没有讨论问题中的点是怎么找到的。第一种方法从两三个简单的特例入手，发现了规律，在数学上，先看出了规律，在证明的话，我们可以使用课本中讲的Mathematical induction，数学归纳法来证明下。

我们还是继续从特例入手分析，从（0,0）到（1,0）需要的最小步数是1，如果去了又回，出现往返，那步数就多了。因此原点到（x, y）所需的最小步数为（|x|+|y|），因此我们可以找到一个步数n的下边界，这个下边界和终点的坐标有一定的关系。这个式子就是通过n步路径可到达的任何点必须满足L2(n)的第一个条件。

|x|+|y|<n

因为毕竟是一个在格点上移动的问题，我们来看下每动一次，对点或是位置有什么样的影响。每次我们从一个格点移动到相邻格点时，（x+y）的奇偶性要么从偶数变为奇数要么从奇数变为偶数。举个例子解释下：从（0,0）到（-2,1）点，最短的步骤就是3步，如果你想2不到达，那真是做梦了。4步不可以，6步不可以，偶数步都不可以。5步，7步，9步，奇数都可以，说明你可以来回走，往返走，兜圈走。上边的分析，从初等数论的角度出发，我们可以理解为：（x+y）这个坐标的和和步数n（可以的步数）是同模2的，也就是（x+y）和n分别除以2，余数都是相同的。这意味着每个点都可以通过n步路径实现也满足下式:

x+y≡n(mod2)

Let L2(n) be the set of lattice points (x, y) in the plane that satisfy |x|+|y|<n and x+y=n(mod2).

The original problem, then, asks us to compute how many points are in the set L2(10). We wish to prove that L2(n) contains (n+l)2 points. Clearly, |L2(1)|=4(where |L2(1)| represents the number of elements in L2(l)), since the points are {(1, 0),(-1, 0), (0, 1), and (0, -1)}. We can likewise verify

that |L2(2)|=9 by listing all 9 points:

L2(2) = {(0, 0), (2, 0), (-2, 0), (0, 2), (0, -2),(1,1),(1,-1),(-1,1),(-1,-1)}

Assume that for k<n, |L2(n)|=(n+l)2.

Now, L2(k+1) is the set of integer solutions to |x|+|y|<k+1 and x+y=k+1(mod2). Note that the points included in L2(k) will not be solutions for the (k+1) case, because they have the wrong parity (even or odd). For instance, the point (k, 0) is in the set L2(k) but not in the set L2(k+1). To proceed by induction, we will need to find a relationship between the (k+l)st case and previous cases. We observe that L2(K-1)⊆L2(K+1).

The points in L2(k+1) that were not already in L2(k-1) are the points whose minimum distance from the origin is exactly k+1, that is

L2(k+1)= L2(k-1)∪{(x,y)||x|+|y|=k+1}

We will count how many points are in the set {(x,y)||x|+|y|=k+1} and call this set G2(k+1). First, let us consider the points in quadrant I satisfying the given conditions. These are {(1, k),(2, k-1), (3, k-2),...,(k,1)}. Since there are k points in quadrant I, by the symmetry of the absolute value function, we conclude that there are 4k points not lying on the axes that satisfy the condition. There are 4 points on the axes that we also need to include: (0, k+1), (0, -k-1), (k+1, 0), and (-k-1, 0). This gives us a total of 4k+4 points in the set.

Now, by the inductive hypothesis, |L2(k-1)|=k2. We have

|L2(k+1)|=k2+4k+4=(k+2)2

翰林AMC12课程体系流程图