- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
一道AMC8真题的解法分析和对比
当前盛行的“刷题”模式,是病态的数学教育的一种具体形式。它在加强学生的应试解题能力的同时,极大地削弱了数学研究的能力。长此以往,将危及数学教育的根基。
在前两篇文章《一道AMC8真题的解法分析和对比》和《一道AMC8真题的解法分析和对比(续)》里,我对一道AMC8真题给出了几个解法并做了一些对比和分析。使用这几个解法中的任意一个,都可以完成这道题的作答。然而,以解决一个数学问题的标准,仅仅做到这一步还远远不够。
本文将讨论两个问题。
第一,这几个解法给出的答案,实际上只是“某个(跟“胖十字形”有8个交点的)正方形”的面积。但是,我们并没有确定,这个正方形就是所有正方形中面积最大的那个。
第二,如果在任意形状的“十字形”内部作正方形,最大面积都是唯一确定的,那么其数值跟“十字形”的形状数据之间是否有确定的关联性?换句话说,是否有计算最大面积值的计算公式(公式中只包含跟“十字形”的形状有关的数量)?
为叙述方便,下面称这个“十字形”为M。
先不考虑“面积最大”的要求,只是在M中作正方形,可以作出很多不同的正方形。这些正方形有的是“正着”摆的,有的是“斜着”摆的。对于后者,我们可以认为是把前者旋转一个角度得到的。
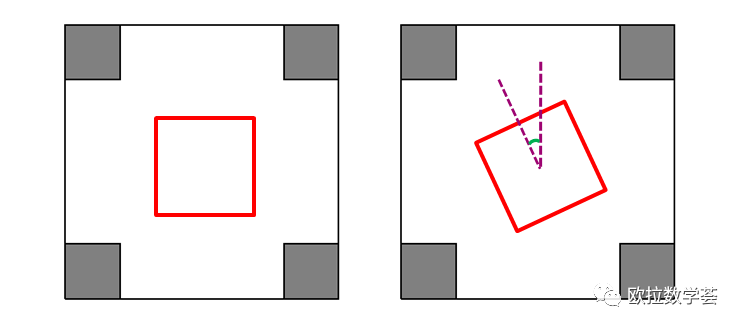
结论一:每个正方形都由三个要素唯一确定:中心点O,旋转角的大小s,边长L。
要根据这“三要素”作出唯一确定的正方形,我们可以先标出中心点,再根据旋转角过这个中心点作一条轴线,最后根据边长大小把正方形画出来。
为了探索正方形的面积最大可以达到多大,在选定中心点以及旋转的角度后,我们再逐渐增加边长,直到触碰到边界为止。
显然,在选定中心点位置O和旋转角度s后,按上述方法确定的“最大面积”的正方形是唯一的。我们记这个正方形为Q(O,s)。
现在我们调整一下顺序,先取定旋转角度s。然后,每选择一个中心点位置O,就得到相应的唯一“最大面积”正方形Q(O,s)。
结论二:对于给定的旋转角度s,在所有正方形Q(O,s)中,O位于M的中心点的那个正方形Q(O,s)是面积最大的。
从直观上不难理解这个结论。证明思路如下:如果选定的O不是位于M的中心点,那么在作出Q(O,s)后,把Q(O,s)平移,使得它的中心点移动到M的中心点位置。这个新的正方形仍然在M内,而且在保持中心点和旋转角度不变的情况下,边长还有可能再增大。
根据结论二,我们要寻找的面积最大的正方形,其中心点必定位于M的中心点。因此,只需要再比较不同旋转角度下的“最大面积”正方形的面积。
尽管旋转角度的取值范围是从0度到360度,但根据对称性,我们只需考虑s在0度到45度之间的情形。下面具体计算Q(O,s)的边长。
记初始的大正方形边长为a,四个角上切去的正方形边长为b。注意到每个Q(O,s)都不能再继续“扩张”了,所以它们要么是边触碰到了M的凹顶点(如下图中的四个紫色点),要么是角触碰到了M的边,也可能两种触碰同时发生。
下面先考虑第一种触碰的情形。
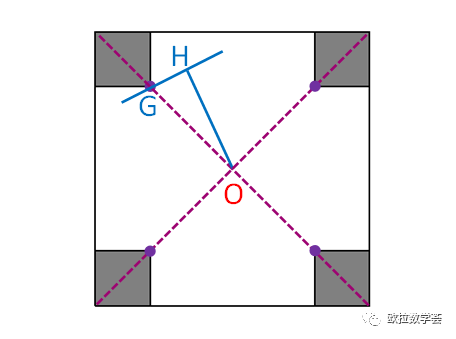
设GH是Q(O,s)的一条边,其中OH垂直于GH。
可知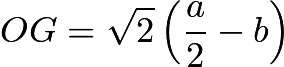 ,
,![]() 。
。
因为![]() ,
,
所以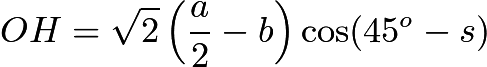 。
。
注意到OH是Q(O,s)边长的一半,所以Q(O,s)的边长不大于OH的两倍,即![]() 。
。
接下来考虑第二种触碰的情形。
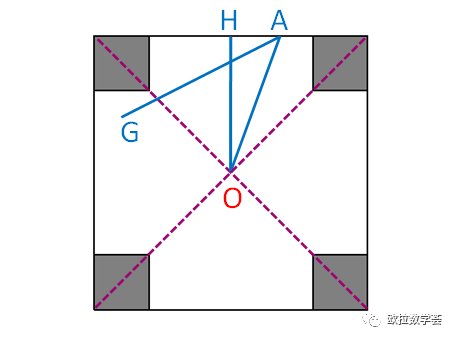
设A是Q(O,s)的其中一个顶点,且位于M的一条边上。作OH垂直于M的这条边,垂足为H。
则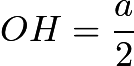 ,
,![]() 。
。
所以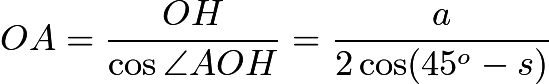 。
。
注意到Q(O,s)的边长是OA的![]() 倍,
倍,
所以Q(O,s)的边长不大于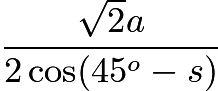 。
。
综合以上两种情形的分析,可知Q(O,s)的边长不大于![]() ,
,
其中,
![]() ,
,
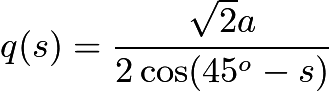 。
。
(1) 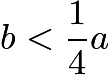 ,即
,即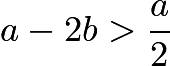 。
。
当![]() 时,
时,![]() 的边长不大于
的边长不大于
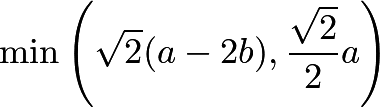
因为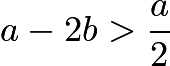 ,所以上式中应取第二项作为最小值。
,所以上式中应取第二项作为最小值。
当s逐步减小时,因为余弦函数的值从0度到45度逐渐减小,所以p(s)的值递减,而q(s)的值递增。
取s的值使得p(s)=q(s),且记s的这个特殊值为![]() 。我们来证明
。我们来证明![]() 就是面积最大的正方形。
就是面积最大的正方形。
当![]() 时,
时,![]() ,Q(O,s)的边长应取q(s),所以比
,Q(O,s)的边长应取q(s),所以比![]() 的边长
的边长![]() 小。
小。
当![]() 时,
时,![]() ,Q(O,s)的边长应取p(s),也比
,Q(O,s)的边长应取p(s),也比![]() 的边长
的边长![]() 小。
小。
最后,我们来计算![]() (也是
(也是![]() )的值。由
)的值。由![]() 推出
推出
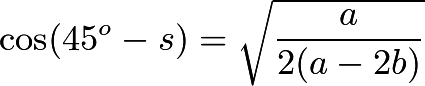
所以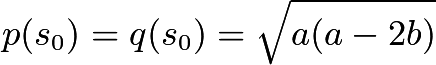 ,因而最大面积为
,因而最大面积为![]() 。
。
在AMC真题中,a=5,b=1,所以最大面积为![]() 。
。
(2) 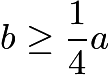 ,即
,即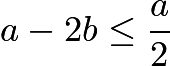 。
。
当![]() 时,
时,![]() 的边长不大于
的边长不大于
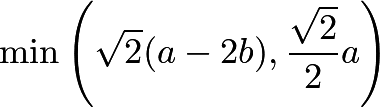
因为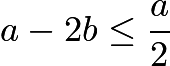 ,所以上式中应取第一项作为最小值。
,所以上式中应取第一项作为最小值。
接下来让s逐步减小到0度,在这个过程中p(s)的值递减,而q(s)的值递增。因此对任意s,p(s)都不大于q(s),所以Q(O,s)的边长始终取p(s)的值。
因为p(s)的值在45度时达到最大值![]() ,所以面积最大的Q(0,s),旋转角度必定是45度,且其面积为
,所以面积最大的Q(0,s),旋转角度必定是45度,且其面积为![]() 。见下图。
。见下图。
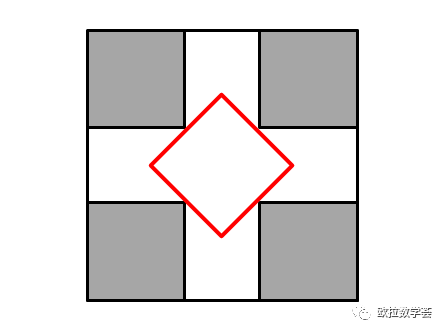
总结一下我们上面得到的结论。
当四个角上被切掉的小正方形边长小于原大正方形的四分之一时(b<a/4),所得的十字形比较“胖”。此时,十字形内可作的正方形的最大面积为a(a-2b),且它与十字形有8个交点。
当四个角上被切掉的小正方形边长大于等于原大正方形的四分之一时,所得的十字形比较“瘦”。此时,十字形内可作的正方形的面积为![]() ,且其旋转角都是45度。
,且其旋转角都是45度。
就推理过程而言,上面的推理省略了一些步骤。在补齐这些步骤后,这就是对问题的一个很完整的数学分析,同时也回答了文章开头所提的两个问题。
本文的分析推理过程,也提供了一个简明的做数学研究的演示范例。如果抱着“做题”的心态,只要根据当前的题目条件找到一个解题路径,最终得到“正确的答案”,就算是大功告成了。大多数人所理解的“解题能力”,就是这样的能力。
而数学研究强调的是思考所寻求的答案和题目的条件之间有什么样的关联性,讲究的是对答案有更全面和深入的了解。并且,还要追问所揭示的关联性中,有哪些是反映了本质关系的,哪些是特殊情形下的“巧合”。换句话说,就是考虑更一般的情形。
正常的数学教育,以培养解题能力为肇始,进而带动数学研究能力的提高;从而,数学学习表现优秀的学生,能够自然地进入数学研究的阶段。病态的数学教育,只关注学生在考试中的解题表现,甚至为了更高效地实现这个目标而禁止学生把时间浪费在“与解题无关”的思考上,这实质上是在削弱学生的数学研究能力。
当前盛行的“海量刷题”的数学学习模式,就是病态的数学教育的一种具体形式。一方面,学生们在日趋白热化的升学竞争中拼尽全力,力求挖尽自己的解题能力;另一方面,他们根本没有精力提升自己的数学研究能力。结果就是,高分学生的数学研究能力不断下降。
数学解题能力和研究能力的“剪刀差”现象,是需要非常警惕的问题,其危害性将危及数学教育的根基。

最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1









