丘成桐中学数学奖中的魔方问题

2018年丘成桐中学科学数学金奖论文是“群论和五魔方”，作者用群论知识解出了五魔方的群结构，给出了求解五魔方的算法。

五魔方（megaminx）是一个正十二面体，每个面是一个正五边形，原始状态下每个面各有一个颜色，一共有12个不同的颜色（还有一种五魔方有6个不同的颜色）。五魔方玩法和三阶魔方一样，通过旋转各面恢复原始状态，只是难度更大。

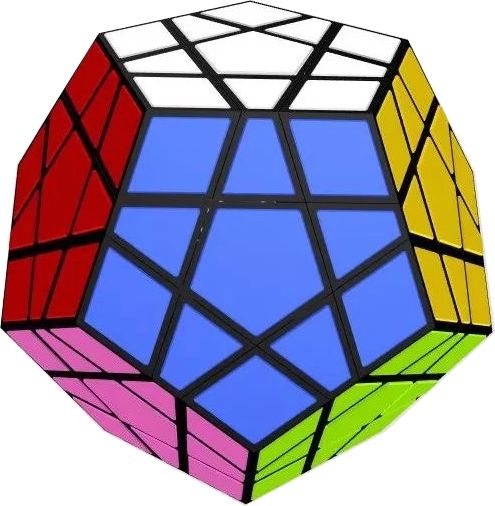
图片来自获奖者论文[1]

五魔方的群结构与三阶魔方有所不同，不过研究方法相同，如果掌握了三阶魔方群的研究方法，不难导出五魔方的群结构，因此适合中学生研究。

三阶魔方（以下简称魔方）是一款世界流行的玩具，由26个可见的小立方块组成一个立方体，原始状态下立方体六个面各有一个颜色，通常是红、橙、蓝、绿、黄和白（见下图）。旋转魔方的任意一个面或中间层，会改变魔方的颜色分布，经过一系列随机旋转后原始状态被打乱，玩家需要旋转魔方恢复原始状态。

图片来自纽约现代艺术博物馆https://www.moma.org/collection/works/2908?artist_id=5069&locale=zh&page=1&sov_referrer=artis

匈牙利建筑学教授厄尔诺·鲁比克（Ernö Rubik）在1974年发明了魔方，起初只是为了寻找一种由很多可动部件组成且任意活动都不会散架的结构，后来他发现魔方可以当玩具玩，于是在1975年申请了专利。1980年初在Ideal Toy公司的推广下成为风靡全球的玩具，并且有了新名字叫鲁比克立方体（Rubik's Cube）。

1981年Douglas Hofstadter在《科学美国人》杂志上撰文详细介绍了魔方，促进了魔方的流行，他本人用了7个月累计花费50个小时复原了魔方。从1980年到1983年全球卖出了约2亿个魔方，是魔方历史上最疯狂的时刻。 

为什么魔方令大众着迷？一个原因是魔方能够产生数量巨大的不同状态，大约有4.3×1019个。这么多状态如果一秒钟数100万个也要140万年才能数完，因此每个人拿到的魔方状态可能都不一样，看似简单然变化无穷，容易上手却琢磨不透。

图片来自文献[4]

魔方也吸引了数学家的注意，John Conway 很早就有了一个魔方，David Singmaster 在1978年8月的国际数学家大会上见到了魔方，迫不及待地用一本书换来一个，然后花了两周时间找到了复原魔方的通用方法。Singmaster在复原中设计了一套标记，并且运用了数学中的群论，他总结成书，在1980和1981年多次出版[2]。根据Singmaster的算法，只需要几分钟就可以复原魔方。

Singmaster的书在1981年卖出了5到6万本，不过跟另一本书比起来就是小巫见大巫了。James G. Nourse是斯坦福大学化学系员工，在1980年圣诞节前买了一个魔方，本打算作为圣诞节礼物送人，没想到自己竟然在节日期间复原了魔方，于是写了本书讲解他的复原方法[3]。Nourse更没想到的是这本书在1981年卖出了668万本，成为当年最畅销的书籍。

Christoph Bandelow 随后也出版了一本书，介绍了魔方群的数学结构[4]。Bandelow 还讨论了魔方的变体，除了立方体形状外还有正四面体，正八面体，正十二面体（五魔方）和正二十面体，这五个正多面体统称柏拉图立体(Platonic solids)，是全部的正多面体。

正多面体魔方有很多变化，比如二阶魔方、四阶魔方（Rubik’sRevenge）、五阶魔方（Professor’s Cube）,金字塔魔方（Meffert's Pyraminx）等等。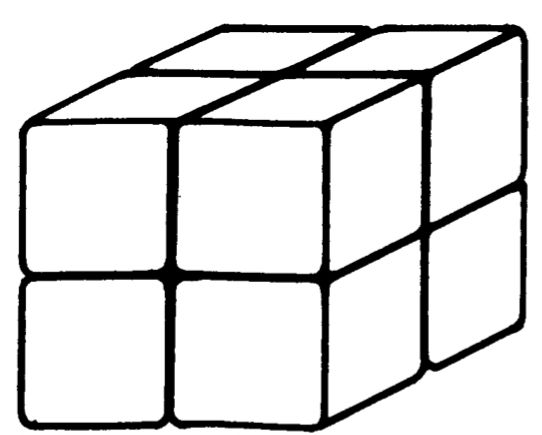 

二阶魔方  Meffert's Pyraminx图片来自文献[4]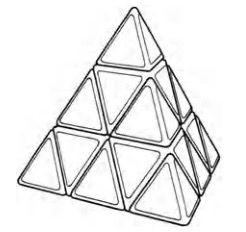 

 

1982年魔方无论是复原方法，还是数学理论，都有了很大进展，除了一个重要问题还没有解决，即Singmaster提出的上帝之数，也就是复原任意状态的魔方所需最小步数的上界。Morwen B. Thistlethwaite给出了一个不超过52步的算法，将这个上界限制在52步以下。

大众的狂热没有坚持多久，到1982年底开始渐渐退去。对数学家来说，魔方把抽象的群论可视化，是非常好的教学和科研工具[5]。普林斯顿数学系教授曼纽尔·巴尔加瓦(Manjul Bhargava)在读研究生的时候，经常坐在宿舍里摆弄着一个特殊的二阶魔方，魔方的8个角块有八个字母a,b,c,d,e,f,g,h，代表8个整数，他觉得这个2×2×2结构的魔方中隐藏着高斯复合问题(gauss composition)的秘密，努力地寻找答案。

无论是玩魔方，还是研究魔方，都离不开对魔方的标记。Singmaster根据魔方每个面所处的位置用字母L(左面)、R(右面)、F(前面)、B(后面)、U(上面)、D(底面)表示，然后根据人们的操作习惯定义任意面顺时针旋转90度为基本操作，用各面字母的黑体L,R,F,B,U,D表示，逆时针旋转90度则表示为L',R',F',B',U',D'。

有了标记后，描述魔方的旋转就非常方便。比如L表示L面顺时针旋转90度，(L')2表示L面逆时针旋转180度，DFD'F'表示从左至右依次执行D、F、D'、F'操作。

魔方每个面有9个小正方形，六个面一共有54个小正方形，原始状态下54个小正方形处在各自的位置上，对应一个排列，不妨记作1，2，3，……，54。一个操作是一个置换，变换魔方上小正方形的位置，得到一个新的排列。理论上这样的排列有54！（54！=1×2×3···×53×54）个，对应54！个状态。

实际上操作魔方得到的状态远没有这么多。54个小正方形分布在6个中心块，8个角块和12个棱块上，如下图阴影部分所示，每个中心块分到一个小正方形，每个角块有3个、棱块有2个。

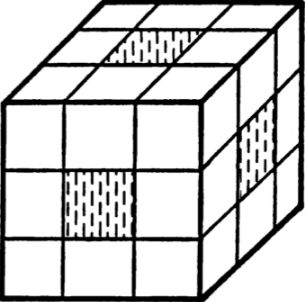
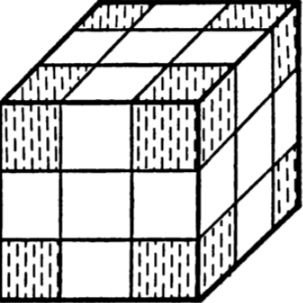
旋转魔方的任意面，角块和棱块的位置发生改变，而中心块位置不变。如果旋转中心块所在的中间层，等价于逆向旋转相邻的两个面，因此理论上只需要考虑面的旋转就行了。

6个位置不变的中心块的颜色代表魔方各个面的颜色，从而魔方的状态只由角块和棱块决定。由于角块变到角块，棱块变到棱块，因此8个角块所有可能的位置有8！个，12个棱块所有可能的位置有12个。

每个角块的三个小正方形在角块转动中可能产生顺时针或逆时针旋转，导致3个不同的定向，同样每个棱块会产生2个不同的定向(两个小正方形的对换)，因此所有可能的状态有8！×12！×38×212个，其中能够由原始状态通过操作魔方得到的状态只有十二分之一，也就是8！×12！×37×210个，约 4.3×1019个。这些状态称为原始状态的轨道，也就是全部的有效状态。
五魔方有20个角块，30个棱块，有效状态有20！×30！×319×227，约1068个，远远多于魔方。

群是一个常用的汉字，表示聚集在一起的人或物，数学上群被抽象成一个非空集合，集合中的元素可以是数，也可以是矩阵、置换等，并且还有一个单位元、每个元素有逆元，任意两个元素之间服从一种运算，满足结合律且运算结果仍然在集合中。全部整数的集合对于加法运算就是一个群，0是单位元。

魔方中的很多操作都可以构成群。比如由操作R得到的集合{R,R2,R3,I} 就是一个群，其中单位元是I，满足R4=I。可以证明，魔方所有操作的集合构成一个群，称为魔方群。魔方群中的运算是复合运算，假设M1，M2是魔方群中的两个操作，它们的复合M1M2表示对魔方先进行M1操作，再进行M2操作，有时复合运算用符号表示为M1·M2。类似的，五魔方有五魔方群。

在2014年魔方诞生40周年之际，一篇发表的学术文章宣告了上帝之数的解决[6]，这个数是20，也就是从魔方的任意一个有效状态恢复到原始状态最多不超过20步（这里的一步使用half turn metric度量，指面旋转90度或180度都算一步）。在这一年召开的国际数学家大会上，曼纽尔·巴尔加瓦获得了菲尔兹奖，委员会在介绍他的工作时写到，“巴尔加瓦相信有更好的方法解高斯复合问题。然后有一天，他在玩魔方时，找到了答案。

参考文献
[1]http://www.yau-awards.science/wp-content/uploads/2018/11/Gerald-Jiarong-Xupaper_1402.pdf
[2]David Singmaster， Notes on Rubik's Magic Cube, 1981.
[3]James G. Nourse，The Simple Solutions to Cubic Puzzles，1981.
[4]Christoph Bandelow, Inside Rubik's Cube and Beyond, 1982.
[5]J. Chen, Group theory and the rubik's cube, Lecture Notes.
[6]Tomas Rokicki,et al.,The Diameter of the Rubik’s Cube Group is Twenty. SIAM J. DISCRETE MATH. Mathematics Vol. 27, No. 2, pp. 1082–1105.