数学Pure Mathematics Numerical Methods总结

Numerical Methods中涉及到的画图问题。考纲中对这个知识点的描述如下：

 

我们不但要会用这个知识点中涉及到的公式求方程的近似解，还要会画出图像来演示能否求出近似解。下面我们通过知识点复习和例题讲解来具体说明。

Part 1知识点复习

Numerical methods 这一章介绍了两种求方程近似解的方法。第一种是Iteration formula, 即递推公式。第二种是Newton-Raphson method, 一种特殊的递推公式。

01Iteration formula

这个方法的整体思路如下：

我们不用考虑g(x)的形式，因为考试时都会给出来x=g(x)的表达式，我们只需由f(x)=0变形到x=g(x)即可。然后我们可以根据题中给出的起始值x0,反复带入计算器来求出后续的值，从而得到精确到一定位数的近似解。

这种方法能否得到方程f(x)=0的近似解（root)取决于x=g(x)的形式。有些变形后的递推公式能得到近似解，我们称：The iteration will converge (收敛）to a root. 有两种图形可以展示这个过程，这两种图形的画法需要掌握，很有可能在考试中出现。

第一种是Staircase diagram 即阶梯图。

 

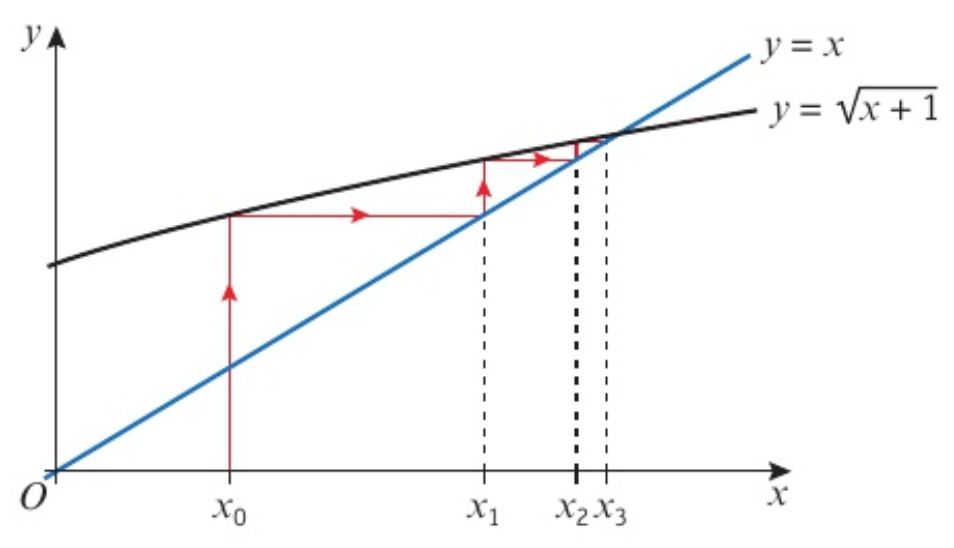
第二种是cobweb diagram 即蛛网图

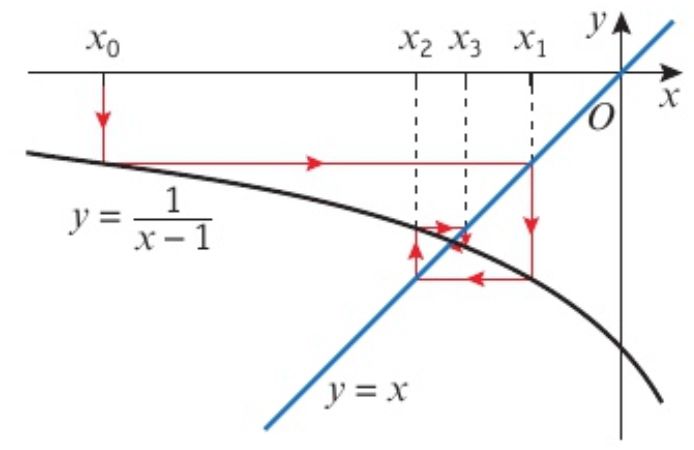
但是有些变形后的公式会使得求出的值越来越远离真实根，我们称：The iteration will diverge (发散）.

02Newton-Raphson method

这个方法有一个具体的公式，考试的公式表中也会给出来。

这个方法是反复利用f(x)在某一点的切线与x轴的交点来逐渐逼近方程分f(x)=0的根。如下图所示：

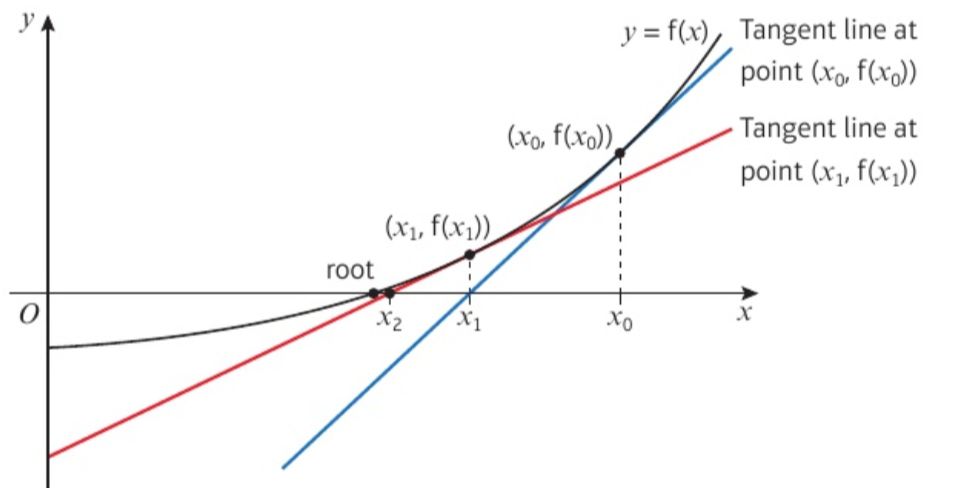
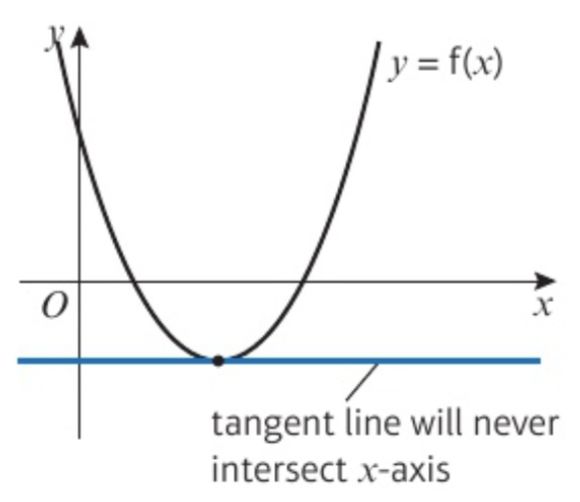
但这个方法也可能得不到近似解。当选取的x0的值在turning point 时，公式中的分母等于0，方法就失效了。如图所示：

这些细节在考试中都可能会考得到。下面我们通过三个例题来具体说明这一块儿知识点的考法。

Part 2例题讲解

1

分析：

(a)问考查一个知识点：

我们只需计算f(1）和f(2)的值即可证明。

(b)问考查用计算器带入递推公式求值。

(c)问考查画图。

解答：

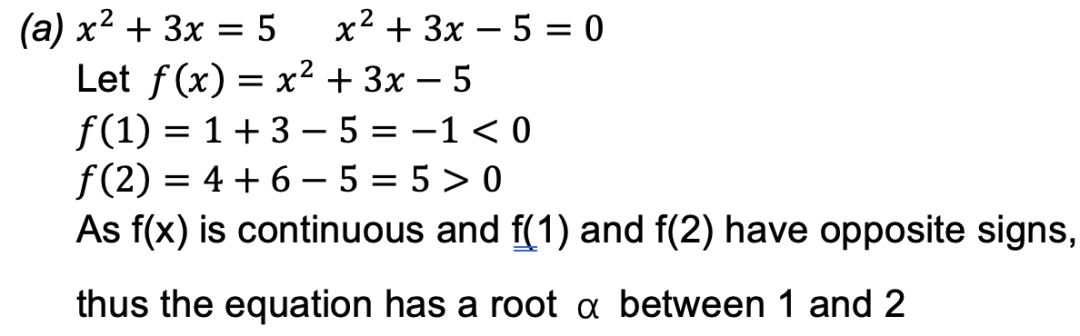
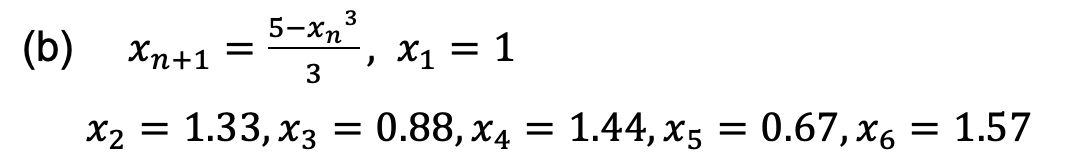
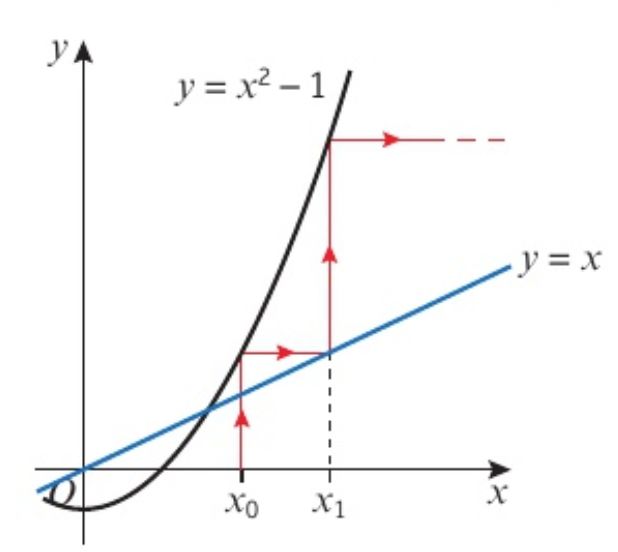
(c)

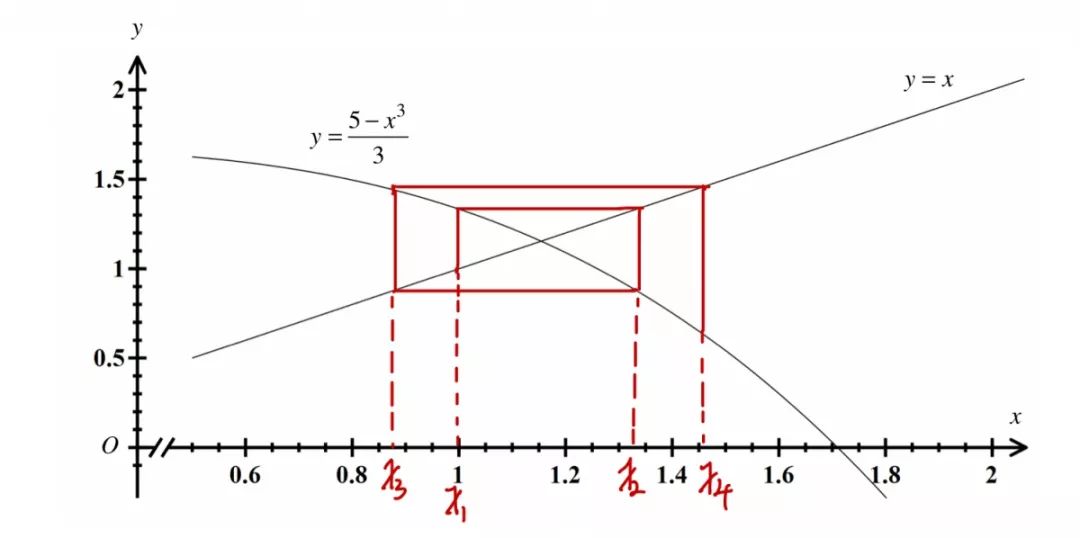
This iteration will diverge away from the root.

2

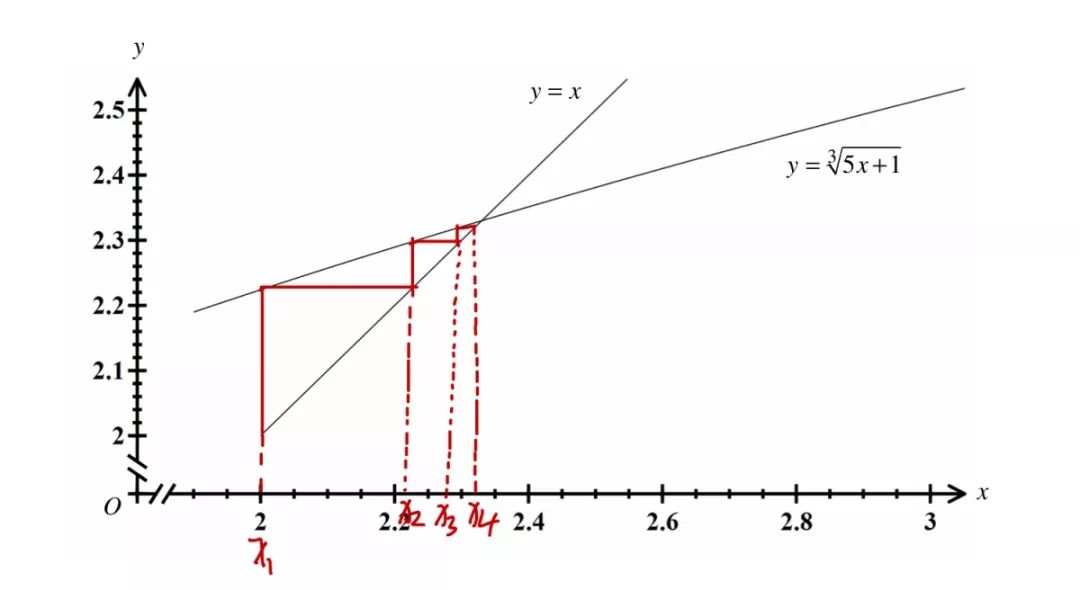
(a) (b)两问同上面例题做法相同，留给同学们自己做。

(c)问的画法如下图所示：

3

分析：

(a)问解释在turning point处的x值为何不能作为递推公式的起始值。(b)问考查递推公式的计算。(c)问还是考查区间两端的函数值变号时，在区间内有根。但这个题需要我们选择合适的区间。比如：

解答：