AMC10/12试题分析之2008AMC12A25数列与矩阵

2008AMC12A25数列与矩阵

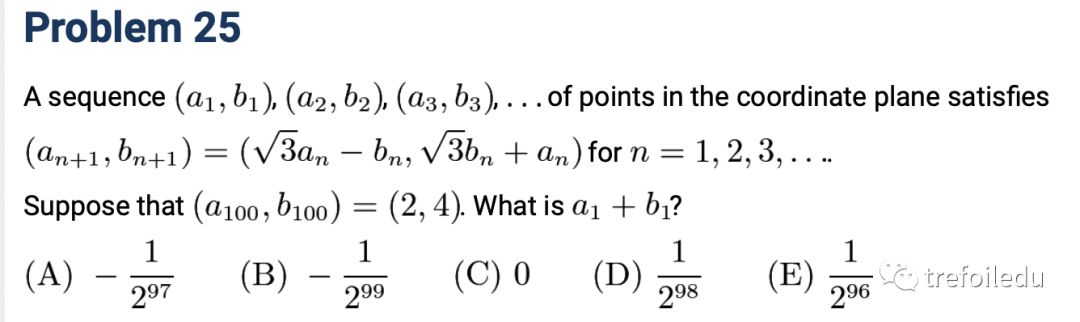
题目用递推关系定义了一个序列，我们先来理解这个递推关系：

由(1)易知：

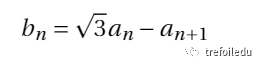
将(2)代入(1)，得：

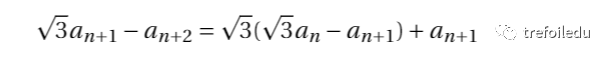
化简得到：

由(2)得：

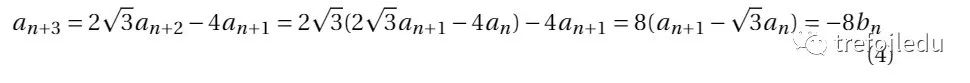
同理，

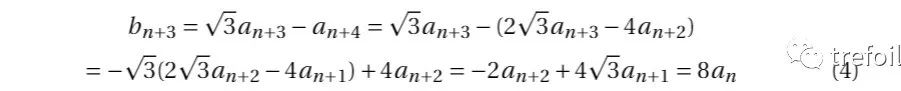
因此，

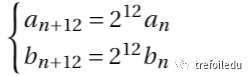
所以：

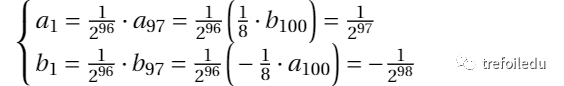
所以：

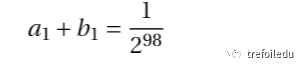
故选D.

我们都知道，很多AMC的学术活动题有这样的特点：如果仅借助现阶段的知识体系，往往解法很繁琐。这是因为这类题目往往来自高等数学知识点的前置，如果掌握了该前置的知识点，就能得到出人意料的简洁解法。以这道题目为基础，我们希望一起感受矩阵的妙用。

首先，请大家观察递推关系：

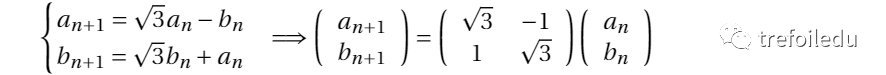
我们发现，该递推关系可以用一个2*2矩阵来表示，而且每个2*2矩阵与  到  的线性变换一一对应。由于逆时针旋转 角对应的矩阵为：

因此，顺时针旋转 角对应的矩阵为：

因此，逆时针旋转度角对应的矩阵为：

在这种观点下，我们发现题目中给出的递推关系的矩阵可表示为：

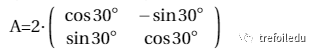
因此，

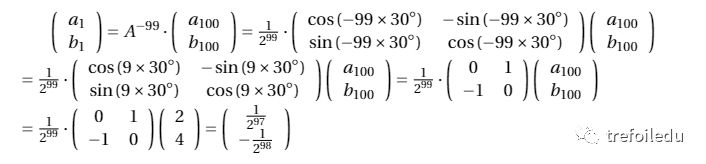
至此，我们把一个看似很复杂的数列问题转化成线性变换的问题，然后用矩阵的工具加以解决，避免了繁杂的运算。经过这个例子，我们得以一窥矩阵的作用。本题中，我们用到了线性变换与矩阵的一一对应关系，实际上，对这一问题，数学家们有更深入的认识，例如，可逆线性变换与可逆矩阵的一一对应关系，进一步的，可逆线性变换的全体构成一个群，我们称之为一般线性变换群。而一般线性变换群是群论表示理论以及代数学中至关重要的一个工具，数学家们用它去刻画各种群变换的表示，以及给各种重要的代数做分类。