USACO 2019 US Open Contest, Silver Problem 3 Fence Planning

Farmer John's NN cows, conveniently numbered 1…N1…N (2≤N≤1052≤N≤105), have a complex social structure revolving around "moo networks" --- smaller groups of cows that communicate within their group but not with other groups.

Each cow is situated at a distinct (x,y)(x,y) location on the 2D map of the farm, and we know that MM pairs of cows (1≤M<105)(1≤M<105)moo at each-other. Two cows that moo at each-other belong to the same moo network.

In an effort to update his farm, Farmer John wants to build a rectangular fence, with its edges parallel to the xx and yy axes. Farmer John wants to make sure that at least one moo network is completely enclosed by the fence (cows on the boundary of the rectangle count as being enclosed). Please help Farmer John determine the smallest possible perimeter of a fence that satisfies this requirement. It is possible for this fence to have zero width or zero height.

INPUT FORMAT (file fenceplan.in):

The first line of input contains NN and MM. The next NN lines each contain the xx and yy coordinates of a cow (nonnegative integers of size at most 108108). The next MM lines each contain two integers aa and bb describing a moo connection between cows aa and bb. Every cow has at least one moo connection, and no connection is repeated in the input.

OUTPUT FORMAT (file fenceplan.out):

Please print the smallest perimeter of a fence satisfying Farmer John's requirements.

SAMPLE INPUT:
7 5
0 5
10 5
5 0
5 10
6 7
8 6
8 4
1 2
2 3
3 4
5 6
7 6

SAMPLE OUTPUT:
10

Problem credits: Brian Dean

---

中文版

Farmer John的NN头奶牛，编号为1…N1…N（2≤N≤1052≤N≤105），拥有一种围绕“哞网”，一些仅在组内互相交流却不与其他组进行交流的奶牛小组，组成的复杂的社交网络。

每头奶牛位于农场的二维地图上的不同位置(x,y)(x,y)，并且我们知道有MM对奶牛(1≤M<105)(1≤M<105)会相互哞叫。两头相互哞叫的奶牛属于同一哞网。

为了升级他的农场，Farmer John想要建造一个四边与xx轴和yy轴平行的长方形围栏。Farmer John想要使得至少一个哞网完全被围栏所包围（在长方形边界上的奶牛计为被包围的）。请帮助Farmer John求出满足他的要求的围栏的最小可能周长。有可能出现这一围栏宽为0或高为0的情况。

输入样例：

7 5
0 5
10 5
5 0
5 10
6 7
8 6
8 4
1 2
2 3
3 4
5 6
7 6

输出样例：

10

供题：Brian Dean

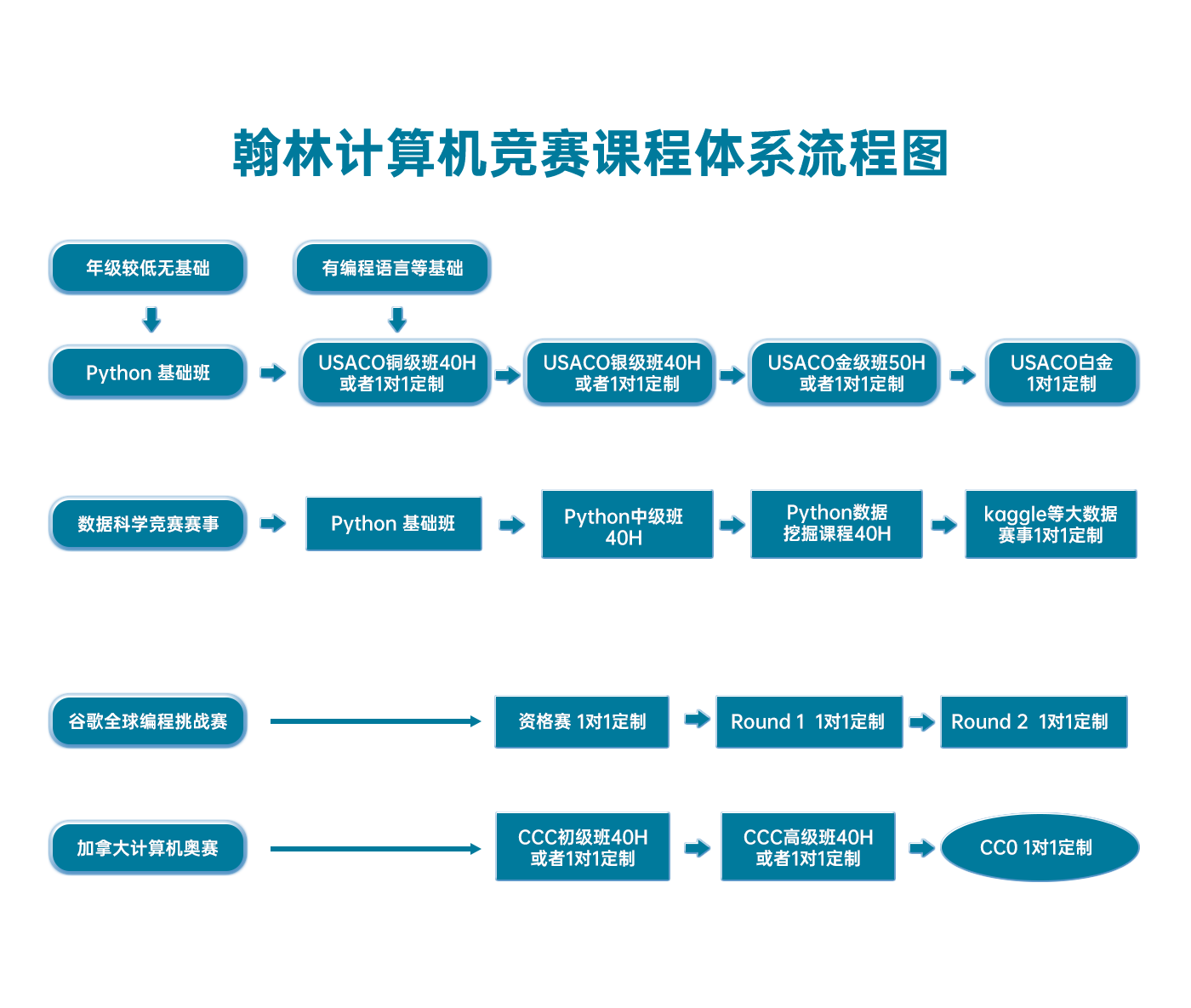
翰林USACO课程体系流程图