Problem 1

The arithmetic mean of the nine numbers in the set  is a -digit number , all of whose digits are distinct. The number  does not contain the digit

Problem 2

What is the value of

when ?

Problem 3

For how many positive integers  is  a prime number?

Problem 4

Let  be a positive integer such that 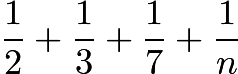 is an integer. Which of the following statements is not true:

Problem 5

Let  and  be the degree measures of the five angles of a pentagon. Suppose that  and  and  form an arithmetic sequence. Find the value of .

Problem 6

Suppose that  and  are nonzero real numbers, and that the equation  has solutions  and . Then the pair  is

Problem 7

The product of three consecutive positive integers is  times their sum. What is the sum of their squares?

Problem 8

Suppose July of year  has five Mondays. Which of the following must occur five times in August of year ? (Note: Both months have 31 days.)

Problem 9

If  are positive real numbers such that  form an increasing arithmetic sequence and  form a geometric sequence, then is

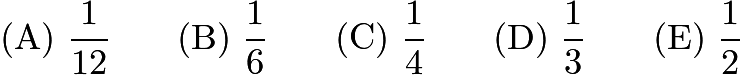
Problem 10

How many different integers can be expressed as the sum of three distinct members of the set ?

Problem 11

The positive integers  and  are all prime numbers. The sum of these four primes is

Problem 12

For how many integers  is 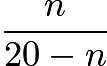 the square of an integer?

Problem 13

The sum of  consecutive positive integers is a perfect square. The smallest possible value of this sum is

Problem 14

Four distinct circles are drawn in a plane. What is the maximum number of points where at least two of the circles intersect?

Problem 15

How many four-digit numbers  have the property that the three-digit number obtained by removing the leftmost digit is one ninth of ?

Problem 16

Juan rolls a fair regular octahedral die marked with the numbers  through . Then Amal rolls a fair six-sided die. What is the probability that the product of the two rolls is a multiple of 3?

Problem 17

Andy’s lawn has twice as much area as Beth’s lawn and three times as much area as Carlos’ lawn. Carlos’ lawn mower cuts half as fast as Beth’s mower and one third as fast as Andy’s mower. If they all start to mow their lawns at the same time, who will finish first?

Problem 18

A point  is randomly selected from the rectangular region with vertices . What is the probability that  is closer to the origin than it is to the point ?

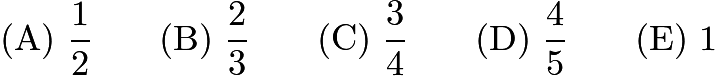
Problem 19

If  and  are positive real numbers such that  and , then  is

Problem 20

Let  be a right-angled triangle with . Let  and  be the midpoints of legs  and , respectively. Given that  and , find .

Problem 21

For all positive integers  less than , let

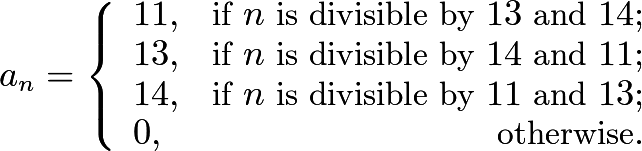
Calculate .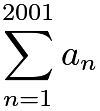

Problem 22

For all integers  greater than , define 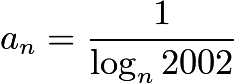. Let  and . Then equals

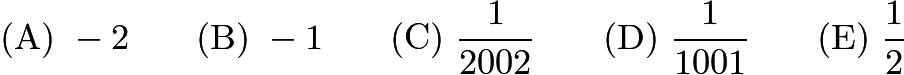
Problem 23

In , we have  and . Side  and the median from  to  have the same length. What is ?

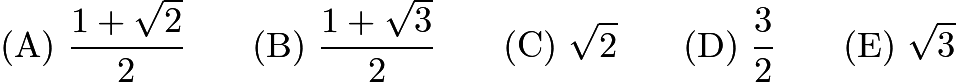
Problem 24

A convex quadrilateral  with area  contains a point  in its interior such that . Find the perimeter of .

Problem 25

Let , and let  denote the set of points  in the coordinate plane such thatThe area of  is closest to