数学最终学什么？

美国的数学学术活动对于大部分的中国孩子而言，除了语言上的障碍外，题目本身的难度并不高，尤其对于中国被称为“学术活动党”的这批孩子而言，更是小菜一碟。但是，我很喜欢解美国数学学术活动题。因为在我看来，判断题目的好坏并不在于题目本身的难度，而在于从题目中我们可以学到多少数学思维。在数学思维的训练方面，我认为美国的数学学术活动是有其过人之处的。

让我先从一道简单的美国数学学术活动题开始。题目大致是这样的：请问下图中至少有一个点接触到外边界的三角形占了所有三角形数量的百分之几？

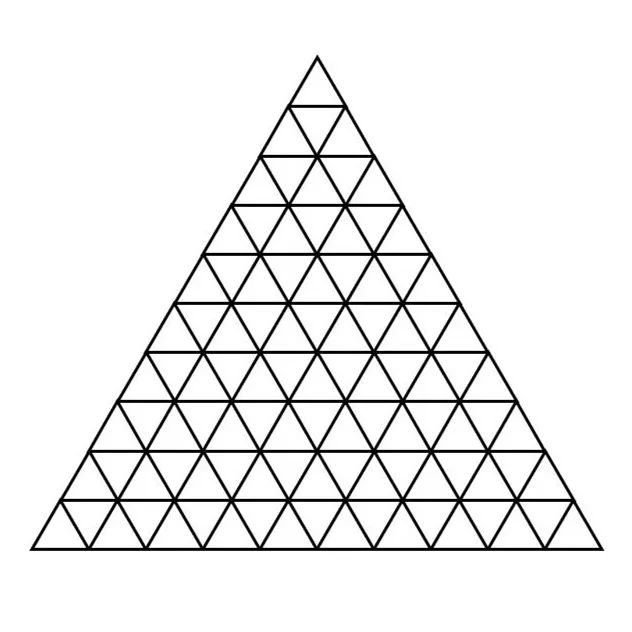
这似乎是个非常简单的题。当然，对于答案而言确实再简单不过了。这里唯一有那么一点难度的，无非就是很多人读不懂题目，无法理解什么叫做“至少有一个点接触到外边界”这句话。当然，还有人理解为要计算各种边长的三角形数量，这个似乎把问题复杂化了。这里我们暂且只考虑最小的那种三角形。

我先来解释这句话。我们知道，三角形由三条直线所构成，三条直线同时产生了三个角，顾名思义叫做“三角形（triangle）”。那么，显而易见的是，下面的三角形是符合题目要求的。

这里很容易忽视的情况是，下面的这些三角形也同样是符合题目要求的：

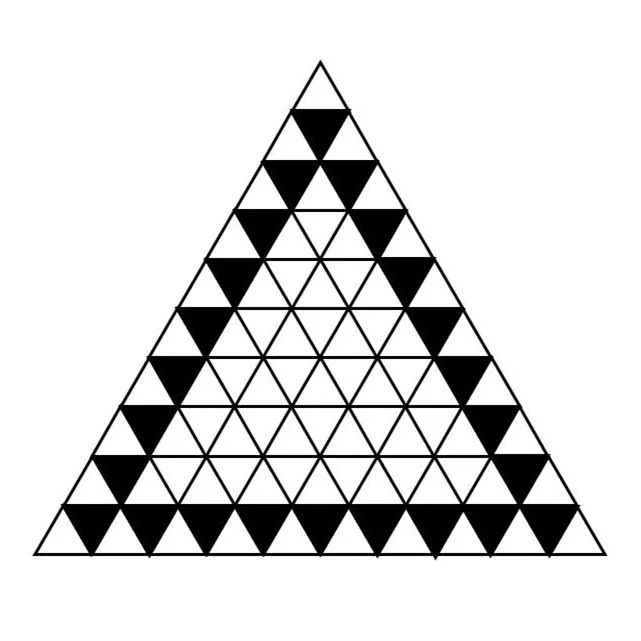
清楚了题目的意思，问题就变成简单的数数了。但往往越是简单的问题，越容易成为真正的问题。这道题我给很多孩子做过，但我发现他们很多人都是一个一个在数，这显然并非出题者的本意。让我从计算全部的小三角形开始说起。

如何计算全部的小三角形数量呢？我们可以从几个不同的角度来思考这个问题。

解法一：最常规的思路，直接每层的三角形数加总求和。我们观察发现，这是一个10层由等边三角形堆积而成的图形。第一层1个三角形，第二层3个三角形，第三层5个三角形，……，第十层19个三角形。于是，问题就变为进行等差数列“1＋3＋5＋…＋17＋19＝”求和了。对于大部分孩子而言，这是很简单的高斯求和问题，答案是：（1＋19）×10÷2＝100个。假如孩子熟悉平均数移多补少的思想，直接用这10个数字中间的两个数9和11的平均数来计算：（9＋11）÷2×10＝100个，也可以得到同样的结果。

解法二：按照三角形的形状分步计算，先计算△形状的三角形，再计算▽形状的三角形，最后两者相加求和。△形状的三角形数为：1＋2＋3＋…＋9＋10＝55个；▽形状的三角形数为：1＋2＋3＋…＋9＝45个；两者相加：55＋44＝100个。

解法三：大胆探索，寻找规律。对于等差数列“1＋3＋5＋…＋17＋19＝”，大部分人的做法无非是解法一中的两种方法，要么高斯求和，要么用平均数的思想。其实，这里还有更加巧妙的计算方法。由于这是一个累加的计算，那么我们来寻找一下累加的过程中可以发现什么有趣的规律呢？我把累加过程做了一个表格。

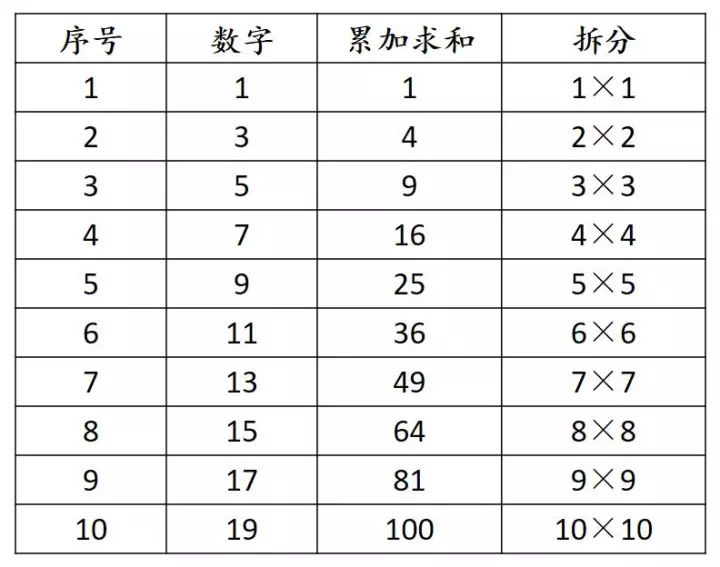
我们经过计算发现，最后的结果居然是一个平方数。这是一个重要的发现，因为这意味着哪怕问题变为20层、50层、100层甚至更多的三角形堆积，我们同样可以快速而又准确地知道全部三角形的数量。这可能是这道题最重要的启发之一。

那么为何“1＋3＋5＋…＋17＋19＝”求和会是一个平方数呢？我们看下面的图形应该马上可以明白其中的原因了，证明过程可谓是“proof without words”。

知道了如何快速计算这个结果，我们再回头看如何计算题目所要求的“至少有一个点接触到外边界的三角形”数量。这里同样有不同的角度可以进行计算。

解法一：因为这个堆积而成的大三角形本身也和小三角形一样，是一个等边三角形，那么我们只要计算其中一条边就可以了。先计算△形状的三角形，数量有10个，因为有10层；▽形状的三角形是穿插在两个△形状的三角形中间，熟悉间隔问题的同学们很快可以报出答案，是9个。于是，每条边上符合题目要求的三角形有：10＋9＝19个。因而，三条边一共有19×3＝57个。这里容易忽略的是边与边之间还有重复计算的三角形数，每个角有两个三角形是重复计算的，故而有3×2＝6个三角形是重复计算的，需要减去。因此，符合“至少有一个点接触到外边界的三角形”数量为57－6＝51个。于是，最终的答案就是：51÷100＝51%。

解法二：通过全部三角形数量减去不符合条件的三角形数量而得到答案。前面已经计算，全部的三角形数一共是100个。那么不符合条件的三角形数量有几个呢？我们观察发现，不符合题目条件的三角形是一个7层小三角形堆积而成的形状，因此根据我们前面发现的规律，一共有：7×7＝49个。两者相减为：100－49＝51个。同样可以得到答案。

通过如此简单的一道题目，我们学到了很多的数学知识和思维方式。这就是为什么我认为从启发数学思维的角度来看，美国的数学学术活动题是我喜欢的类型。

再来解一道题，很常见的问题：将一个圆形纸片用直线划分成若干部分，请问：用5条直线最多可将圆形纸片划分成多少部分？

同样，只要多试几次，我们很容易知道答案为16。但是，其实这不重要，这个答案不是这个问题想要传达给我们的知识，重要的是我们要从简单的数字中去发现规律，哪怕最后问题变为10条线、20条线甚至100条线，我们也可以快速回答出来。

题目要求的是5条直线，我们一开始是很难知道16这个答案的，我们需要从简单的数字中去探索规律。1条和2条因为数字太简单，似乎很难发现一般性的规律，那么我们通常选择一个折中的数字，比如3条线。为了发现如何画可以尽可能多地分割这个圆，我给孩子们进行了示范。如下图所示：

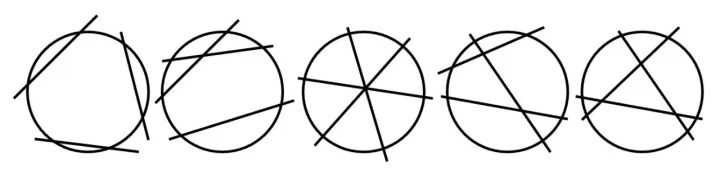
我们经过观察发现，3条线要分割出尽可能多的块数，应该使得新划上去的直线与原有的直线在圆的内部都相交，而且交点要不出现重合。为了让规律来得更加显而易见，我列了一个表格，其中一列为直线数，第二列为分割的快数，第三列为新增的快数，最后一列为我们可以发现的规律。如图所示：

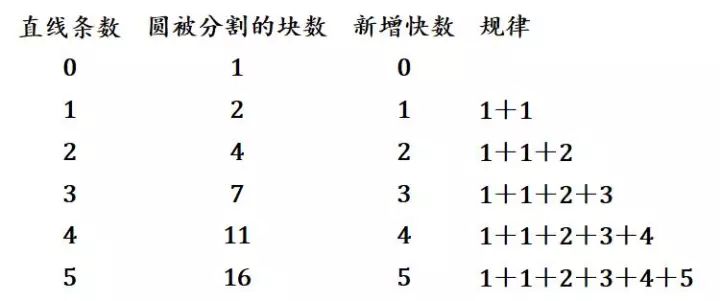
这是一个非常美妙的结果，也意味着哪怕题目要求50条直线甚至100条直线，我们都能马上得到准确的答案。

这两道题之所以拿出来说，是因为我发现，很多孩子学数学只关心答案而不注重思考的过程。我多次说过：答案对很多时候只是巧合，不代表真正理解；思维方式和思考过程对了，答案只是水到渠成的事情。

我们从小学到大学，大部分的数学知识在我们走上社会之后都是用不到的，只有少部分人会用到复杂的数学知识。学习数学，最重要的不是追求那个答案，而是从数学解题过程中我们能得到不断训练的思维能力、推理能力、创造能力，等等。这些才是伴随我们终生的能力，也是学习数学可以给予我们的最重要的东西。

很可惜，现在的教育在这方面做得很糟糕，出现了很多的问题。教孩子机械地背公式、记答案、学解题套路，而忽略了学数学要掌握的最重要的方面。我遇到过一些孩子，看到问题先是告诉我这是“某某问题”，然后背一下这个问题可能会用到的公式。然后，遗憾的是，背完公式之后就没有然后了……还有一些孩子告诉我，他们的老师都是这么教他们的，叫他们必须背公式，从来不问为什么。如果我认同这样的方法，我就不做现在的事情了。

然而，这究竟是为什么呢？我想，很多方面都是值得我们反思的！