怎样学习数学效率会更高？

小学、中学甚至到大学，都得学数学。为什么要学这么多数学呢? 伽利略说：“大自然，这部伟大的书，是用数学语言写成的。”前美国总统科学顾问艾德华·大卫说：“很少人认识到当今如此被广泛称颂的高技术在本质上是一种数学技术。”数学是科学之母，是物理学、力学、天文学、化学、生物学的基础，为其提供了描述规律的语言和探索未知世界的工具。

数学如此重要，怎样才能更高效地学习数学？像数学家那样学习数学才是更高效的学习思维和方法。

一、数学家究竟是如何思考的？

菲尔兹奖得主Atiyah：“我们欣赏数学之美动用到的大脑部分与欣赏音乐、艺术和诗歌时动用的大脑部分完全一样。这是个大发现”。数学家的思考方法到底是怎样的？他们质疑一切；反过来又如何；利用逆否；考虑极端情形；构造自己的例子；假设用在哪里；从复杂的一边开始；如果有……，那么会怎样；交流等。

在学校教育中，老师是如何引导孩子学习数学呢？老师受教育进度和教学计划约束，往往忽略数学中最美的知识。数学中最美的往往是最基本的，最基本的往往不会在考试中出现。为了实施教学计划，老师们往往会对这些最美的知识一笔带过，很少能认真领着孩子欣赏这些美的知识。天真烂漫的孩子能够在私下的生活中能慢慢琢磨和感受这些美的数学知识的人，是少之又少的。名校往往把这些任务压给孩子们，悟性高的往往勉强应付，悟性低的遗害终生。另外，如今的孩子们，都是忙碌的孩子，家长早已把孩子们的时间安排的满满的，哪有时间琢磨、欣赏和感受这些美的数学知识。

培训机构模式：例题讲解—习题套。这种模式在降低数学题目难度的同时，剥夺了孩子自己思考和探索的机会。聪明孩子在此教育模式之下，很快能获得理想成绩；普通孩子将会消耗掉自己的兴趣和动力。一旦孩子没有兴趣和动力是非常危险的事情，像现实生活中，有些孩子虽然获得奥数奖牌并成功保送到理想大学，但最终甚至没能顺利拿到学位进而被劝退。

坚持学数学的孩子，靠其内心的标准，也靠他们在数学直觉上的微小收获所带来的巨大喜悦。

培育和激发孩子的探索精神，是教育中的重要任务。探索精神是数学家以及其他科学家所具备的重要精神。美国和俄罗斯在探索性教学方面积累了丰富的成功经验，培育了大量的著名数学家和科学家。探索性教学有两种道路：一是之字形，爬起来不累，适合游客和大部队；二是攀岩，爬行者会觉得累而快。下面举靖学习数学过程中的一个例子：

如图，O为三角形ABC中的一个点。O到三角形三边的垂线分别交三条边于D、E、F。设线段OA、OB、OC的长度分别是x、y、z，线段OD、OE、OF的长度分别是p、q、r，那么埃尔德什-莫德尔不等式为：

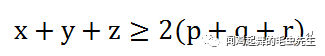
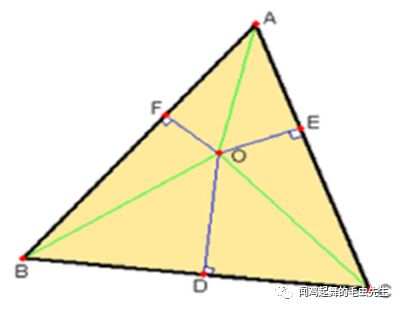
这个题目是高中学术活动数学课本《数学（高中上册）》（华东师范大学第二附属中学（实验班用））第五章的内容。靖第一次拿起这本书时，前面的内容都没学习过，随意翻到这一页，就被这道题目给迷住了。

第一次看这道题目时，靖很平静地告诉我，他看不懂解题过程。我说：“看不懂就看不懂，没关系，前面铺垫的很多知识你都没学，怎么可能能看懂呢？很多符号你都不认识。”

过了几天，靖第二次禁不住又找到这本书，又翻到这道题目，又看了一遍，很平静地告诉我，他没看懂解题过程。我答：“看不懂，没关系，以后再想办法。”放下书出去玩玩吧！我以为靖早已忘了这道题目。

又过了几天，靖第三次翻到这个题目，他看懂了，而且很激动很热情地告诉我：“这道题目我看懂了。”我一脸笑容地说：“给我讲讲。”结果，靖就给我先做了知识铺垫，把所有可能用到的定理和知识先给我讲了一遍，然后才讲这道题目的证明过程。

又过了几天，靖第四次告诉我：“他已经会用至少五种方法证明这道题目。”

靖这个题目的学习过程，就是典型的探索性学习过程。他走的路径是攀岩式路径。

像数学家那样学习数学：学习教材时，自己先思考例题，如果不会再看例题讲解；如果题目的结论变成条件，条件变成结论，会怎样；改编题目，自己出题，也是一种很好的思路。这种学习数学的思路会让孩子有更强大的动力和兴趣去探索，持续维护孩子的兴趣，提升学习效率。

以靖为例，靖在幼升小那个暑假，花了大约10天的时间，完全像个小数学家那样，无论是出去玩还是洗脚或洗脸，一直在思考数学问题。在这个过程中，他是不是平跑过来向我确认他思考的结果的正确性，然后满意地离开。

例1：2+2+2+2+2+2=？这也是6个2相乘呀！说明12里有6个2。在此，我明白了整数的加减乘除运算规则。

例2：4x25=100，8x12.5=100，16x6.25=100，这三个算式就是一个乘数除以2，一个乘数乘以2，结果应该不变。在此，我明白了小数如何进行乘除运算。

 

二、如何刷题效率会更高

刷题的目的是用最短的时间读懂题目和问题，并理清思路，短时间接触大量题型的各种方法。具体方法：将答案放在一边，读题圈数字单位和要点，在第一直觉中给出解题思路。然后对照答案，如果完全一样，直接跳过。如果不一样，对比答案，寻找差异，思考答案的方法好在哪里。最后合上答案在脑子里解一遍题。

第一种刷题：计时练习，常年坚持。把积攒下来的经典题目凑成一张卷子做，这种方法的要义在于常年坚持，不在于某次刷题的多少。

第二种刷题：刷错题本，重视数学难题的消化。针对那些不会做的题，看了答案，没有很好掌握的题。这种题目，需要刷好几遍，才能真正搞会。此种方法的要义在于：坚持，坚持，再坚持。

第三种刷题：小组训练法，提升悟性。两三个人一伙，互相给对方当教练，将大家不会的题，分为三组，每组题由一个人负责看答案，来当其他两人的教练，允许提问，教练给予提示，靠这个过程把题做出来。

刷题的导出效果：学生可以将难题放在脑子里翻来覆去地想，突然有了灵感，也算是内在的随机性的自我奖励。难题相对个人能力不同而不同。通过第一遍刷题，找出难题，再集中精力二刷或三刷难题，悟性和能力必将会有大幅度提升。

 

三、怎样刷题才能刷出“数觉”？

日本菲尔兹奖得主小平邦彦，创造了数觉（NumberSense）这个名词。他提出：了解数学是看出数学的现象来，这种“看”是凭某种感觉来意会的，有数觉的人念起数学来就得心应手得多。“数觉”已被写入西方国家的中小学数学教材中，开始被心理学家研究。

数觉不能简单地理解为对数学的感觉，是人们在实践经验和已有知识的基础上，形成和发展起来的一种认识能力，是持久探索和思考的结果，而不是凭空想象的结果。数觉是人脑对数学对象、结构及其关系的某种直接领悟或洞察。数觉具有突发性、直接性、创造性和或然性特征。

突发性：数觉往往受视觉触发，突然地领悟道理，做出判断，得出结论。直接性：在直觉思维中，数学是一种逻辑的跳跃，通常不作详尽的分析和推理，直接接触结果，因而具有直接性。创造性：数觉思维的结果通常会表现出新的突破，得到新的结论，因此带有极强的创造性。或然性：数觉是一种逻辑的跳跃，没有经过严格的逻辑思考与推理，因此其所得的结论未必正确，具有或然性。

数觉涉及更多非理性因素，即理性之外的认识、意识、心理因素。数觉的培养应重在基于孩子已有的知识经验和生活经验，鼓励孩子经常做实验性数学作业，给孩子创造探索与思考的机会，加强孩子合情推理等能力的培养。

1. 在平时生活中，创设生活数学情境，激发孩子研究数学的兴趣，诱发孩子的直觉思维，促进自觉探究。例如，靖大概5岁时，爸爸随便编了一个题目。

我们一家去饭店吃饺子，要了两盘总计48个，花费同样的时间，爸爸吃3个饺子，妈妈吃2个饺子，靖靖吃1个饺子，问最后，爸爸、妈妈和靖靖分别吃了多少个饺子？

靖靖很快答说：靖靖吃了8个，妈妈吃了16个，爸爸吃了24个饺子。

2. 在平时生活中，适当加大数学知识难度和渗透科学认识的引导，重视孩子对科学方法、科学价值的掌握和理解，加强孩子整理知识和重组知识能力。

例如，如图，半径为5厘米的圆内和圆外各有一个正方形，圆内正方形的四个顶点都在圆周上，圆外正方形的四条边和圆都只有一个接触点。问大正方形的面积比小正方形的面积大多少？

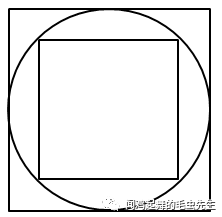
孩子如果受到知识的限制，无法用分别求出大小正方形的边长，在求出面积，最后求出它们的差这种思路。由于圆、正方形都是中心对称图形，圆内接小正方形可以旋转，旋转到特殊位置就能发现图形间的大小关系（如图）。显然，小正方形的面积是大正方形面积的一半。

 

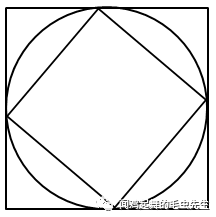
这种引导，有利于孩子探索、发现和解决数学问题，顺利抓住数学知识的本质，提升孩子的数觉水平。

3. 基于孩子已有的知识和经验，重视数学学习材料的选取，营造真是的数学活动教学情境，鼓励孩子做实验性探索。例如，引导孩子学习“统计与概率”知识时，尝试从生活中收集数据，进行整理、统计和分析，从中寻找数学知识与规律。

下表是一次我和孩子玩脉搏测量的实验结果。经过与孩子共同讨论、交流之后发现，测量一个人的脉搏用20~30秒比较适宜。通过做实验，可以激发孩子的数学学习兴趣和好奇心，提升孩子“数觉”能力。

4. 引导合情推理，训练创造性思维。合情推理的基本格式是，首先给出一个猜想，然后通过多种方式找出理由去证实，以增强或否定其猜想的合理性。

给孩子一组不同类型、不同大小的平行四边形，与孩子一起探讨平行四边形的相关性质。用量角器测量四个角，通过对折比较对角大小和对边的大小，通过平移观察对边的平行性质等。这种实践性测量和观察，提升了孩子的感知认识。