2019AIME I 完整真题及答案

2019AIME I真题

考试时间：北美3.13日，2019

Problem 1

Consider the integer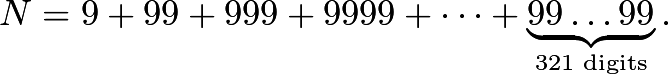Find the sum of the digits of .

Problem 2

Jenn randomly chooses a number  from . Bela then randomly chooses a number  from  distinct from . The value of  is at least  with a probability that can be expressed in the form  where  and  are relatively prime positive integers. Find .

Problem 3

In , , , and . Points  and  lie on , points  and  lie on , and points  and  lie on , with . Find the area of hexagon .

Problem 4

A soccer team has 22 available players. A fixed set of 11 players starts the game, while the other 11 are available as substitutes. During the game, the coach may make as many as 3 substitutions, where any one of the 11 players in the game is replaced by one of the substitutes. No player removed from the game may reenter the game, although a substitute entering the game may be replaced later. No two substitutions can happen at the same time. The players involved and the order of the substitutions matter. Let  be the number of ways the coach can make substitutions during the game (including the possibility of making no substitutions). Find the remainder when  is divided by 1000.

Problem 5

A moving particle starts at the point  and moves until it hits one of the coordinate axes for the first time. When the particle is at the point , it moves at random to one of the points , , or , each with probability , independently of its previous moves. The probability that it will hit the coordinate axes at  is , where  and  are positive integers. Find .

Problem 6

In convex quadrilateral  side  is perpendicular to diagonal , side  is perpendicular to diagonal , , and . The line through  perpendicular to side  intersects diagonal  at  with . Find .

Problem 7

There are positive integers  and  that satisfy the system of equationsLet  be the number of (not necessarily distinct) prime factors in the prime factorization of , and let  be the number of (not necessarily distinct) prime factors in the prime factorization of . Find .

Problem 8

Let  be a real number such that . Then  where  and  are relatively prime positive integers. Find .

Problem 9

Let  denote the number of positive integer divisors of . Find the sum of the six least positive integers  that are solutions to .

Problem 10

For distinct complex numbers , the polynomialcan be expressed as , where  is a polynomial with complex coefficients and with degree at most . The value of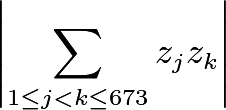can be expressed in the form , where  and  are relatively prime positive integers. Find .

Problem 11

In , the sides have integers lengths and . Circle  has its center at the incenter of . An [i]excircle[/i] of  is a circle in the exterior of  that is tangent to one side of the triangle and tangent to the extensions of the other two sides. Suppose that the excircle tangent to  is internally tangent to , and the other two excircles are both externally tangent to . Find the minimum possible value of the perimeter of .

Problem 12

Given , there are complex numbers  with the property that , , and  are the vertices of a right triangle in the complex plane with a right angle at . There are positive integers  and  such that one such value of  is . Find .

Problem 13

Triangle  has side lengths , , and . Points  and  are on ray  with . The point is a point of intersection of the circumcircles of  and  satisfying  and . Then  can be expressed as , where , , , and  are positive integers such that  and  are relatively prime, and  is not divisible by the square of any prime. Find .

Problem 14

Find the least odd prime factor of .

Problem 15

Let  be a chord of a circle , and let  be a point on the chord . Circle  passes through  and  and is internally tangent to . Circle  passes through  and  and is internally tangent to . Circles  and  intersect at points  and . Line  intersects  at  and . Assume that , , , and , where  and  are relatively prime positive integers. Find .

参考答案(部分)，请登录或注册查看