利用几何变换解一类平几最值问题

处理三角最值问题，在课堂教学中一般多利用基本不等式或建立函数结构来求，但往往运算量较大或设参数不明确,若能从几何角度来思考问题，有时会有意想不到的收获.下面我们从两个问题出发来说明几何变换在求平面几何最值中的应用.

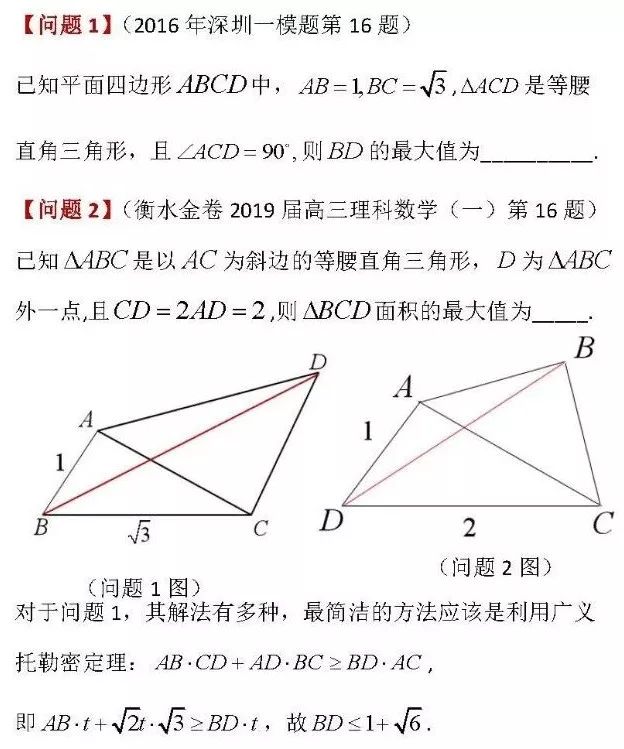
‍但上述方法对于没有学术活动经历的学生而言显得过于高端，仅有结论而缺乏推导过程并没有完整揭示这类问题的本质，比如我们要探究问题2中三角形BCD面积的取范围时，托勒密定理的结论似乎就用不上，问题1和问题2“似乎”变成了两个相对独立的问题.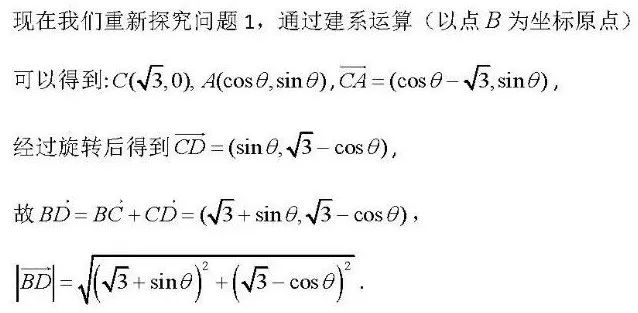

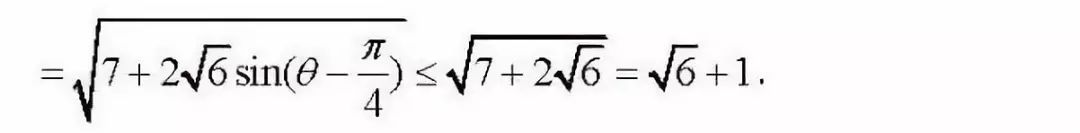
‍从上述代数推导过程中可以发现点D的轨迹应该是一个圆，但该推导过程中运算量会比较大，对学生要求较高，事实上，我们可以通过一个简单的几何图形旋转来说明为什么点D的轨迹是一个圆.

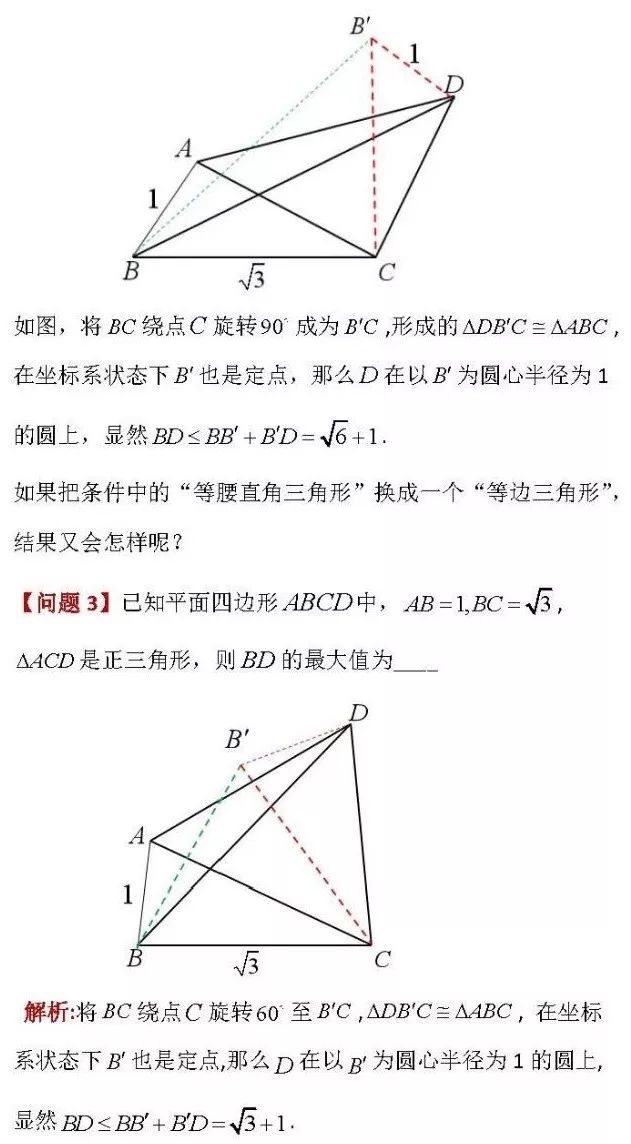
‍相比而言，纯几何途径解决这个问题，明显简洁许多，当然该解法过程实际上也解决了例1中新增的那个问题，即本质上只需要搞清楚动点的轨迹是一个圆，那么长度和面积的最值解法本质是一样的.

以上结果似乎表明，若ACD是一个相对特殊的三角形，用旋转的方法（旋转角度和特殊三角形相关）可以轻松得到BD的最大值和三角形面积的最大值，然而事实并非这么简单，我们再回到问题2.

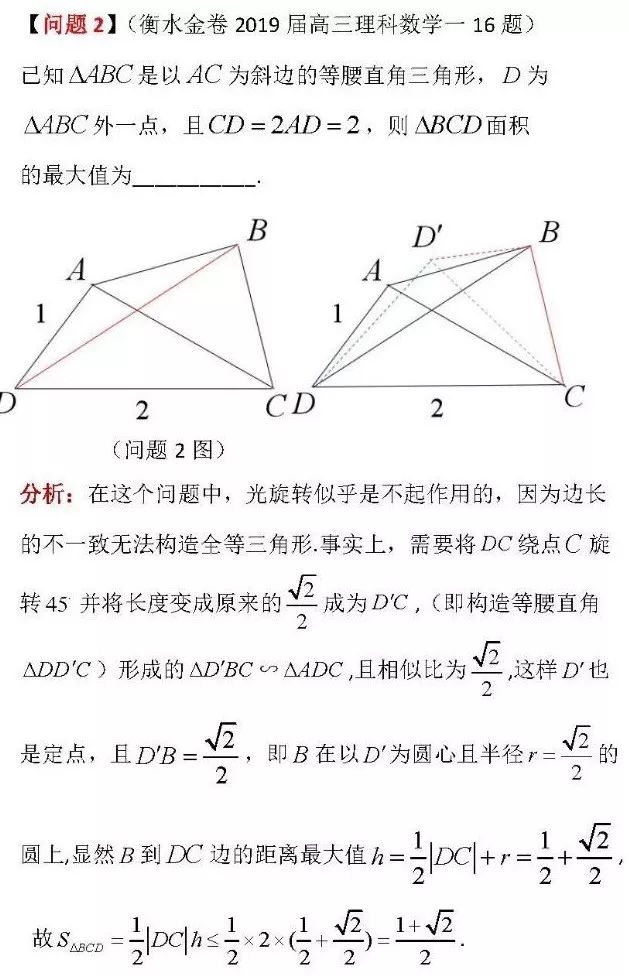
‍这样我们就找到了解决这类问题的一般方法：利用构造局部相似三角形来解决问题，之前的全等构造实际上是此类问题中的一种特殊情况.

在更一般的情况下,利用上述构造相似三角形的思想可以相应得到：

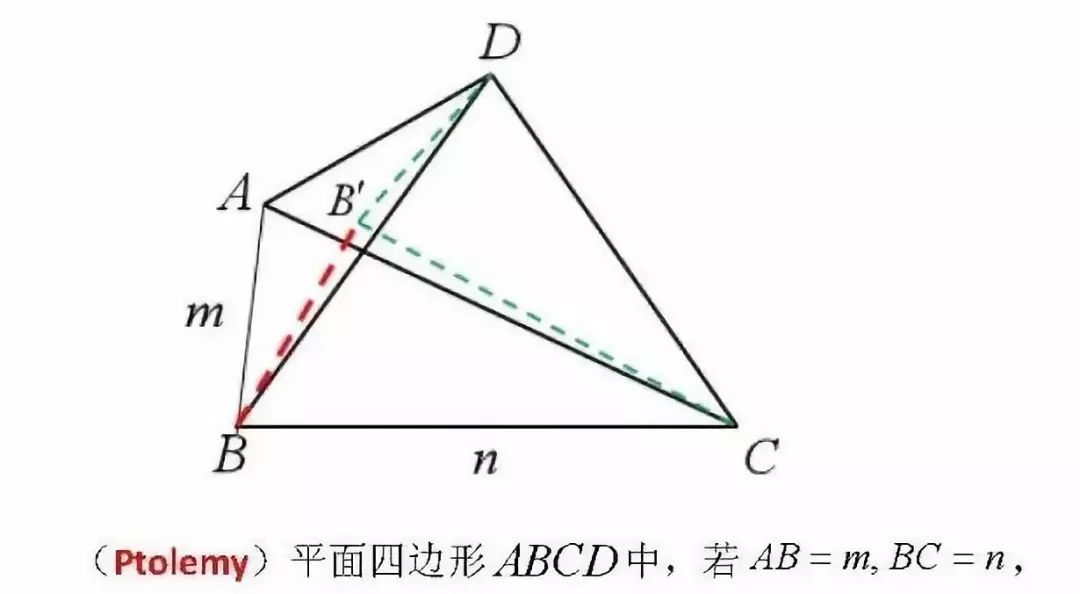
‍此结论即为广义托勒密定理的基本结论，上述几个例题的思考再现了这个经典的平面几何定理的由特殊到一般的生成过程，显然其中的思考过程比最终结论更有利于理解这类问题的本质，如伴生出来的面积最大问题，实际上考虑到三角形BCD的面积最大时，可能会造成A,B,C三点共线从而不能形成四边形，故三角形BCD面积不一定有最大值（事实上，例题1中则三角形BCD的面积就没有最大值），只能有一个取值范围.

在这类三角最值问题的解决过程中，代数方向的思考会出现参数选择的合理性、运算的要求高等诸多问题，而几何方向的思考能体现一种解题的轻巧美，但是往往不容易想到，产生这一问题的原因在于初中教材对平面几何能力的要求过低，而高中现在因为取消了几何证明选讲这个考点导致教师在教学上重视不够，个人觉得很可惜，在建立几何思维的道路上，平时的积累和总结很重要。另外，从代数推断出的结论中多问自己为什么会是这样，能否有几何的解释方法，保持对几何的一颗好奇心，也是研究几何问题的一个良好方法.