2018年黔南州中考数学压轴题分析

【题目】

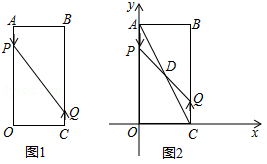
（2018•黔南州）如图1，已知矩形AOCB，AB=6cm，BC=16cm，动点P从点A出发，以3cm/s的速度向点O运动，直到点O为止；动点Q同时从点C出发，以2cm/s的速度向点B运动，与点P同时结束运动．

（1）点P到达终点O的运动时间是　　s，此时点Q的运动距离是　　cm；

（2）当运动时间为2s时，P、Q两点的距离为　  cm；

（3）请你计算出发多久时，点P和点Q之间的距离是10cm；

（4）如图2，以点O为坐标原点，OC所在直线为x轴，OA所在直线为y轴，1cm长为单位长度建立平面直角坐标系，连结AC，与PQ相交于点D，若双曲线y=k/x过点D，问k的值是否会变化？若会变化，说明理由；若不会变化，请求出k的值．

【答案】

 

解：（1）∵四边形AOCB是矩形，

∴OA=BC=16，

∵动点P从点A出发，以3cm/s的速度向点O运动，

∴t=16/3，此时，点Q的运动距离是16/3×2=32/3cm，

故答案为16/3，32/3；

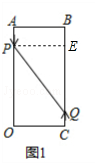
（2）如图1，由运动知，=3×2=6cm，CQ=2×2=4cm，

过点P作PE⊥BC于E，过点Q作QF⊥OA于F，

∴四边形APEB是矩形，

∴PE=AB=6，BE=6，

∴EQ=BC﹣BE﹣CQ=16﹣6﹣4=6，

根据勾股定理得，PQ=6√2，

故答案为6√2；

（3）【方法一】相似法

设运动时间为t秒时，

由运动知，AP=3t，CQ=2t，

同（2）的方法得，PE=6，EQ=16﹣3t﹣2t=16﹣5t，

∵点P和点Q之间的距离是10cm，

∴62+（16﹣5t）2=100，

∴t=8/5或t=24/5；

（4）K的值不会变化，理由：

∵点P、点Q运动时间想到，速度比是3:2，

∴AP/CQ=3/2，

∵AO//BC，∴∠PAD=∠QCD，∠APD=∠CQD，

∴△APD∽△CQD，

∴AD/AC=3/5，

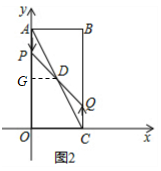
过点D作DG⊥y轴垂足为G，

∴∠AGD=∠AOC=90°且∠GAD=∠OAC，

∴△ADG∽△ACO，

∴GD/OC=AG/AO=AD/AC=3/5，

即GD/6=AG/16=3/5，

∴GD=18/5，AG=18/5，

∴OG=AO-AG=16-48/5=32/5，

∴点D坐标为（18/5，32/5），

∵点D在双曲线y=k/x上，

∴k=18/5×32/5=576/25．

【方法二】函数法

k的值是不会变化，

理由：∵四边形AOCB是矩形，

∴OC=AB=6，OA=16，

∴C（6，0），A（0，16），

∴直线AC的解析式为y=﹣8/3x+16①，

设运动时间为t，

∴AP=3t，CQ=2t，

∴OP=16﹣3t，

∴P（0，16﹣3t），Q（6，2t），

∴PQ解析式为y=(5t-16)/6x+16﹣3t②，

联立①②解得，x=18/5，y=32/5，

∴D（18/5，32/5），

∴k=18/5×32/5=576/25是定值．

【总结】

本题最后一问不难，但是也不容易．题目问及反比例函数k的值是否会发生变化时，我们想到的肯定是不变．

那么根据这个不变，我们可以得出什么呢？

有两种情况，一种就是它们的交点为定点，则k必然不变，另一种则是交点的横纵坐标满足某个等量关系，例如相乘等于一个定值k，也可以得到k是不变的．

所以这时候大家就感觉有点不值所措了．

比较容易想到的方法是“方法二”，假设知道PQ的直线解析式，求出交点坐标即可，但是明显此种方式比较难算．

如果大家通过选取几个特殊时间t，代入求出交点之后就知道是第1钟还是第2种情况了．了解是过定点的时候，那就容易想到方法一了．

因为AO和BC是平行的，所以容易想到相似，利用相似，求出AD的长，再求出点D的坐标即可．