【A-level】进阶数学，分布近似必考知识点讲解！

Statistics作为进阶数学学习中重要的一门科目，一直以来都受到了大部分同学的青睐。由于进阶数学中另一重要的科目Mechanics会涉及到物理学的部分知识内容，而有些同学也是由于不善于物理科目的学习才选择的进阶数学科目，这时候Statistics就会成为这部分同学的首选。

本次和大家一起分享一下统计学里面一个较为重要的知识点：Appropriate approximation between three distributions。这里指的就是Binomial distribution，Poisson distribution ，Normal distribution，即二项分布，泊松分布与正态分布之间的分布近似。

首先：我们对这三个分布要极其熟悉。整体来说可以将这三个分布分为两大类，属于离散数据分布的二项分布与泊松分布以及属于连续数据分布的正态分布。

对于二项分布和泊松分布来说，我们需清楚地知道符合两个分布的各个条件，这不仅关系到我们对一道题目属于那种分布的初步判断，还会在文字简答题中结合题目背景来说明为什么题目中的数据分布属于某种分布。

第二点：就是熟练运用相应公式以及会通过表格计算相应题目。

最后一点：要清晰地了解每一种分布的期望值与方差。而对于正态分布，需要会通过公式将一般正态分布转成标准正态分布，以及通过表格解决相应计算题目。

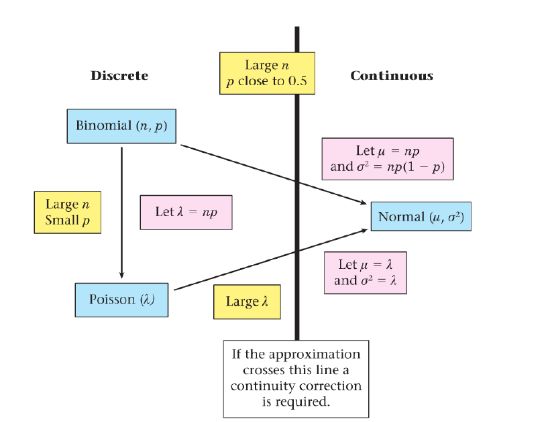
接着我们就可以分析这里存在的3个近似分布了

首先是二项分布近似为泊松分布，这里的两个分布都属于离散数据分布。条件就是较大的n与较小的p，又有一个小窍门就是观察np，也就是二项分布近似为泊松分布之后的期望值亦是方差，由于泊松分布的表格期望值最大为10，所以np会小于等于10.而当我们发现一道题目有着较大的n，p又趋向于1，这时候我们就需要利用二项分布事件的对立事件，通过变换变量的方式来进行泊松分布近似。

二项分布和泊松分布近似为正态分布属于离散数据近似为连续数据，需要进行连续性矫正。这是离散数据近似为连续数据必备的一步，也是大部分同学会遗忘的环节，希望同学们一定要牢记连续性矫正这一步。

二项分布近似为正态分布需要较大的n，且p趋向于0.5，而且我们也通常会发现这时np，也就是二项分布近似为正态分布后的期望值，大于10.再通过公式将一般的正态分布转为标准正态分布，通过表格查得题目的答案。而泊松分布近似为二项分布只需要较大的λ，这时仍需要通过连续性矫正在进行求解。

这类题目既有直接要求通过某种近似求解，也有需要通过对题目的分析来选择合适的近似分布。