- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
USACO 2018 December Contest Platinum Problem 2 Sort It Out
FJ has NN (1≤N≤1051≤N≤105) cows (distinctly identified 1…N1…N) lined up in a row. FJ likes his cows to be sorted in increasing order, but unfortunately they are currently out of order. While in the past FJ has used groundbreaking algorithms such as “bubble sort” to sort his cows, today he is feeling quite lazy. Instead he will yell at a specific cow, one at a time, to “sort it out”. When yelled at, a cow will make sure she is not out of order (from her point of view). While there is a cow immediately to her right with a smaller ID, they will swap places. Then, while there is a cow immediately to her left with a larger ID, they will swap places. Finally, the cow is done “sorting it out”, at which point the cow to her left will have a smaller ID and the cow to its right will have a larger ID.
FJ wants to pick a subset of cows, and then iterate through this subset, yelling at each of them in turn (in increasing order of ID), again and again until all NN cows are sorted. For instance, if he picks the subset of cows with IDs {2,4,5}{2,4,5}, then he will yell at cow 22, and then at cow 44, and then at cow 55. If the NN cows are still not sorted, he will yell at these same cows again, and again, as necessary.
Since FJ is not sure which cows are paying attention, he wants to minimize the size of this subset. Furthermore, FJ thinks that the number KK is very lucky. Help him find the KK-th lexicographically smallest subset of minimal size so that shouting at them repeatedly will eventually result in all cows being sorted.
A subset SS of {1,…,N}{1,…,N} is said to be lexicographically smaller than a subset TT if the list of elements in SS (in increasing order) is lexicographically smaller than the list of elements in TT (in increasing order). For instance, {1,3,6}{1,3,6} is lexicographically smaller than {1,4,5}{1,4,5}.
Scoring: In cases worth 3/163/16 of the points, N≤6N≤6 and K=1K=1. In additional cases worth 5/165/16 of the points, K=1K=1. In additional cases worth 8/168/16 of the points, no further constraints.
INPUT FORMAT (file itout.in):
The first line contains a single integer, NN. The second line contains a single integer KK (1≤K≤10181≤K≤1018). The third line contains NNspace-separated integers, representing the cows’ numbers from left to right.It is guaranteed that there will be at least KK valid subsets.
OUTPUT FORMAT (file itout.out):
The first line of output should contain the size of the minimal subset. The remaining lines should contain the IDs of the cows in the KK-th lexicographically smallest subset of minimal size, with one ID per line, listed in increasing order.
SAMPLE INPUT:
4 1 4 2 1 3
SAMPLE OUTPUT:
2 1 4
We start with the array 4213. After FJ yells at the cow with ID 1, the array will be 1423. When FJ yells at the cow with ID 4, the array will be 1234. At which point, the array is sorted.
Problem credits: Spencer Compton
USACO 2018 December Contest Platinum Problem 2 Sort It Out题解(翰林国际教育提供,仅供参考)
显然剩下的部分相对顺序不会改变。
也就是剩下的部分必须是一个最长上升子序列。
要求操作的字典序第kk小,也就是剩下的部分字典序第kk大。
求字典序第k大的最长上升子序列。
分为两部分来思考。
- 如何求最长上升子序列的个数?
这是一个51nod上的题目,不要用传统的二分,贪心的思路。
换成按值,动态规划,最后用线段树优化的思路。 - 如何找到字典序最大的最长上升子序列?
对于每个数字,如果他能出现在最长上升子序列中,那么他的位置是唯一的。
倒着DP,从第一位向后一位一位的确定即可。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
ll k, inf = 4e18;
int a[262147];
vector<int> b[262147];
pair<int, ll> t[262147];
int v[262147];
pair<int, ll> add(pair<int, ll> a, pair<int, ll> b) {
if (a.first > b.first) {
return a;
} else if (a.first < b.first) {
return b;
} else {
return make_pair(a.first, min(a.second + b.second, inf));
}
}
pair<int, ll> query(int l, int r, int x, int L, int R) {
if (r < L || R < l) {
return make_pair(-1, 0);
}
if (L <= l && r <= R) {
return t[x];
}
int m = (l + r) / 2;
return add(query(l, m, x * 2, L, R), query(m + 1, r, x * 2 + 1, L, R));
}
void change(int l, int r, int x, int p, pair<int, ll> w) {
if (l == r) {
t[x] = w;
return;
}
int m = (l + r) / 2;
if (p <= m) {
change(l, m, x * 2, p, w);
} else {
change(m + 1, r, x * 2 + 1, p, w);
}
t[x] = add(t[x * 2], t[x * 2 + 1]);
}
int main() {
freopen("itout.in", "r", stdin);
freopen("itout.out", "w", stdout);
scanf("%d%lld", &n, &k);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
change(1, n + 1, 1, n + 1, make_pair(0, 1));
for (int i = n; i > 0; i--) {
pair<int, ll> res = query(1, n + 1, 1, a[i], n + 1);
res.first++;
change(1, n + 1, 1, a[i], res);
}
for (int i = 1; i <= n; i++) {
pair<int, ll> res = query(1, n + 1, 1, i, i);
b[res.first].push_back(i);
}
pair<int, ll> ans = query(1, n + 1, 1, 1, n + 1);
int st = 1;
int last = 0;
assert(k <= ans.second);
for (int i = ans.first; i > 0; i--) {
for (int jj = b[i].size() - 1; jj >= 0; jj--) {
int j = b[i][jj];
// if (j < last) {
// continue;
// }
pair<int, ll> res = query(1, n + 1, 1, j, j);
// printf("pre %d %d %d %lldn", i, j, res.first, res.second);
if (k > res.second) {
k -= res.second;
} else {
v[j] = 1;
last = j;
// printf("choose %dn", j);
for (; a[st] != j; st++) {
change(1, n + 1, 1, a[st], make_pair(0, 0));
}
break;
}
}
}
printf("%dn", n - ans.first);
for (int i = 1; i <= n; i++) {
if (!v[i]) {
printf("%dn", i);
}
}
return 0;
}[/hide]
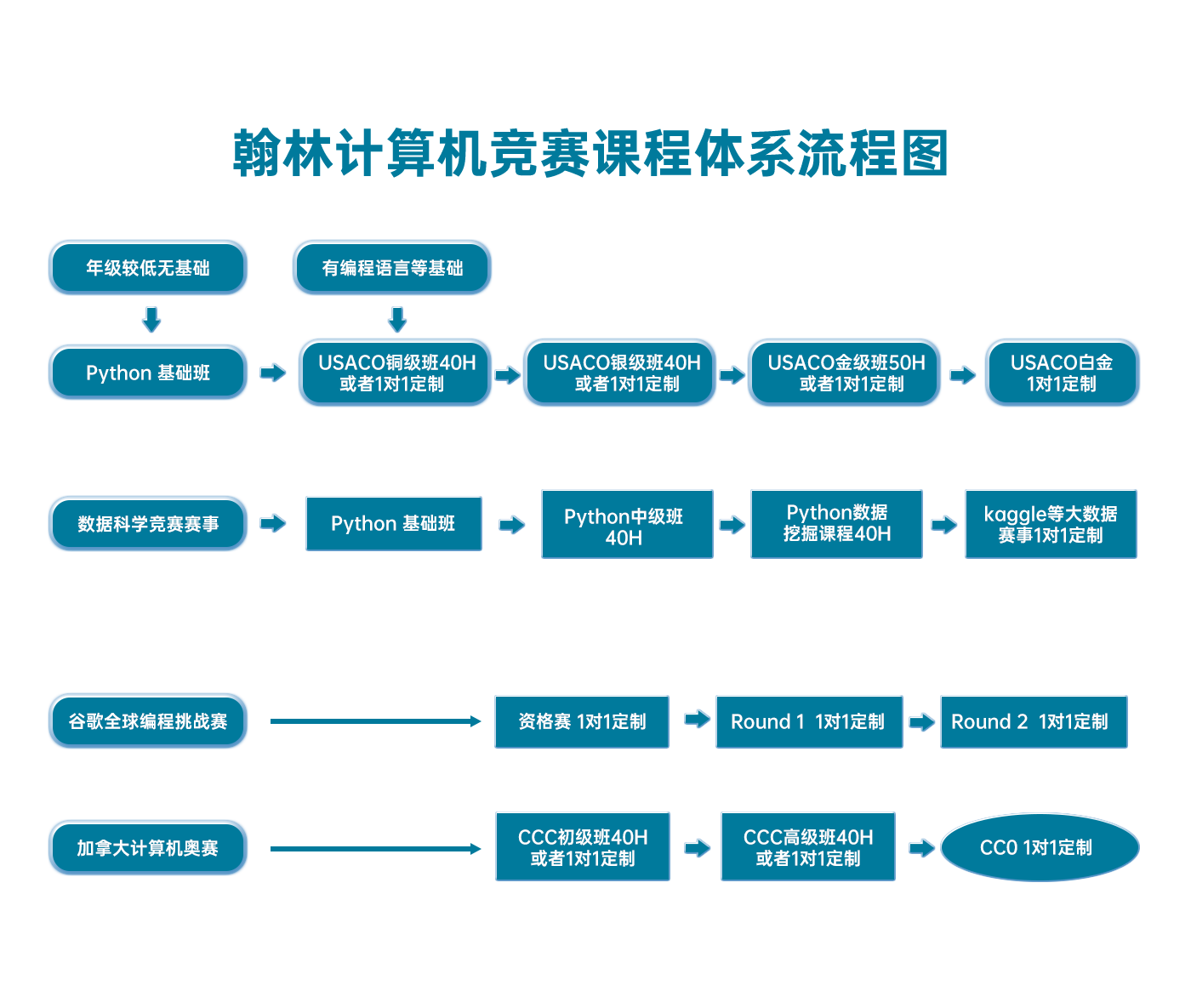
翰林USACO课程体系流程图

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









