- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
USACO 2018 December Contest Silver 3 MOOYO MOOYO
With plenty of free time on their hands (or rather, hooves), the cows on Farmer John's farm often pass the time by playing video games. One of their favorites is based on a popular human video game called Puyo Puyo; the cow version is of course called Mooyo Mooyo.
The game of Mooyo Mooyo is played on a tall narrow grid cells tall ( ) and 10 cells wide. Here is an example with :
0000000000 0000000300 0054000300 1054502230 2211122220 1111111223
Each cell is either empty (indicated by a 0), or a haybale in one of nine different colors (indicated by characters 1..9). Gravity causes haybales to fall downward, so there is never a 0 cell below a haybale.
Two cells belong to the same connected region if they are directly adjacent either horizontally or vertically, and they have the same nonzero color. Any time a connected region exists with at least cells, its haybales all disappear, turning into zeros. If multiple such connected regions exist at the same time, they all disappear simultaneously. Afterwards, gravity might cause haybales to fall downward to fill some of the resulting cells that became zeros. In the resulting configuration, there may again be connected regions of size at least cells. If so, they also disappear (simultaneously, if there are multiple such regions), then gravity pulls the remaining cells downward, and the process repeats until no connected regions of size at least exist.
Given the state of a Mooyo Mooyo board, please output a final picture of the board after these operations have occurred.
INPUT FORMAT (file mooyomooyo.in):
The first line of input contains and ( ). The remaining lines specify the initial state of the board.
OUTPUT FORMAT (file mooyomooyo.out):
Please output lines, describing a picture of the final board state.
SAMPLE INPUT:
6 3
0000000000
0000000300
0054000300
1054502230
2211122220
1111111223
SAMPLE OUTPUT:
0000000000 0000000000 0000000000 0000000000 1054000000 2254500000
In the example above, if , then there is a connected region of size at least with color 1 and also one with color 2. Once these are simultaneously removed, the board temporarily looks like this:
0000000000 0000000300 0054000300 1054500030
2200000000 0000000003
Then, gravity takes effect and the haybales drop to this configuration:
0000000000 0000000000 0000000000 0000000000 1054000300 2254500333
Again, there is a region of size at least (with color 3). Removing it yields the final board configuration:
0000000000 0000000000 0000000000 0000000000 1054000000 2254500000
Problem credits: Brian Dean
USACO 2018 December Contest Silver 3 MOOYO MOOYO题解(翰林国际教育提供,仅供参考)
通过搜索(BFS或DFS)找到连通的区域,然后消去,然后模拟下落。
基本就是 mayan游戏 难度
实现细节:
1. 一般来说DFS比BFS好写,如果可以选的话,建议DFS。
2. 计数和染色部分分开写,如果写在一起,非常麻烦。
3. 下落的部分,有不需要额外数组的写法,建议学习。
#include <bits/stdc++.h>
using namespace std;
int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};
int n, k;
char s[120][12];
bool v[120][12];
bool in(int x, int y) {
return 0 <= x && x < n && 0 <= y && y < 10;
}
int dfs(int x, int y, char c) {
v[x][y] = true;
int re = 1;
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (in(nx, ny) && s[nx][ny] == c && !v[nx][ny]) {
re += dfs(nx, ny, c);
}
}
return re;
}
void color(int x, int y, char c) {
s[x][y] = '0';
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (in(nx, ny) && s[nx][ny] == c) {
color(nx, ny, c);
}
}
}
bool gao() {
bool flag = false;
memset(v, 0, sizeof v);
for (int i = 0; i < n; i++) {
for (int j = 0; j < 10; j++) {
if (!v[i][j] && s[i][j] != '0') {
int sz = dfs(i, j, s[i][j]);
if (sz >= k) {
flag = true;
color(i, j, s[i][j]);
}
}
}
}
return flag;
}
void fall() {
for (int j = 0; j < 10; j++) {
int c = 0;
for (int i = 0; i < n; i++) {
if (s[i][j] != '0') {
s[c++][j] = s[i][j];
}
}
while (c < n) {
s[c++][j] = '0';
}
}
}
int main() {
freopen("mooyomooyo.in", "r", stdin);
freopen("mooyomooyo.out", "w", stdout);
scanf("%d%d", &n, &k);
for (int i = n - 1; i >= 0; i--) {
scanf("%s", s[i]);
}
while (gao()) {
fall();
}
for (int i = n - 1; i >= 0; i--) {
printf("%sn", s[i]);
}
return 0;
}[/hide]
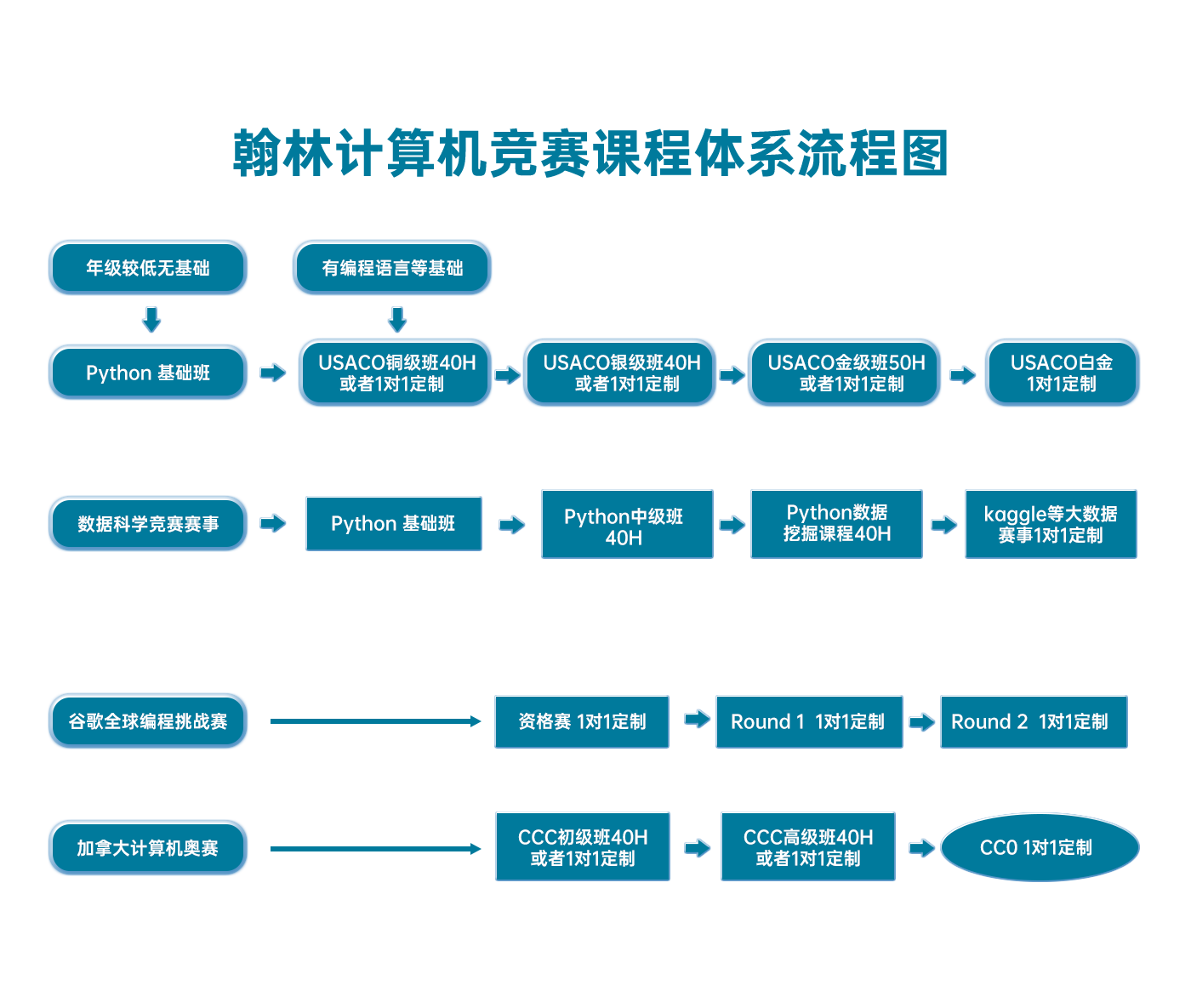
翰林USACO课程体系流程图

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









