- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
USACO 2018 December Contest Gold Problem1 FINE DINING
扫码免费领取学术活动真题及最新消息,获取报名表,咨询最新报名通道
The cows are heading back to the barn at the end of a long day, feeling both tired and hungry.
The farm consists of pastures ( ), conveniently numbered . The cows all want to travel to the barn in pasture . Each of the other pastures contains a cow. Cows can move from pasture to pasture via a set of undirected trails ( ). The th trail connects a pair of pastures and , and requires time to traverse. Every cow can reach the barn through a sequence of trails.
Being hungry, the cows are interested in potentially stopping for food on their way home. Conveniently, of the pastures contain tasty haybales ( ), with the th such haybale having a yumminess value of . Each cow is willing to stop at a single haybale along her trip to the barn, but only if the amount of time this adds to her path is at most the yumminess of the haybale she visits. Note that a cow only "officially" visits at most one haybale for dining purposes, although it is fine if her path takes her through other pastures containing haybales; she simply ignores these.
INPUT FORMAT (file dining.in):
The first line contains three space-separated integers , , and . Each of the next lines contains three integers , , and
, describing a trail between pastures and which takes time to traverse ( and are different from each-other, and is a
positive integer at most )
The next lines each describe a haybale in terms of two integers: the index of its pasture, and its yumminess value (a positive integer at most ). Multiple haybales can reside in the same pasture.
OUTPUT FORMAT (file dining.out):
The output should consist of lines. Line contains the single integer if the cow at pasture can visit and dine on a haybale on the way to the barn, and otherwise.
SAMPLE INPUT:
451 1 4 10 2 1 20 423 235 432 27
SAMPLE OUTPUT:
1 1 1
In this example, the cow in pasture 3 should stop for a meal, since her route would only increase by 6 (from 2 to 8), and this increase is at most the yumminess 7 of the haybale. The cow in pasture 2 should obviously eat the hay in pasture 2, since this causes no change in her optimal route. The cow in pasture 1 is an interesting case, as it may first appear that her optimal route (length 10) would increase too much to justify stopping for the hay. However, she actually does have a route that makes stopping at the hay beneficial: move to pasture 4, then to pasture 2 (eating the hay), then back to pasture 4.
Problem credits: Dhruv Rohatgi
USACO 2018 December Contest Gold Problem1 FINE DINING题解(翰林国际教育提供,仅供参考)
求每个点到终点的距离,显然是从终点反向dijkstra。
第二次把所有haybale的距离初始化为第一次的距离减去收益。
这个值可能是负数,再做一次dijkstra。(边和第一次是一样的)
第二次dijkstra的时候,相当于有多个起点。
如果第一次距离<第二次距离,那么不可能,否则可能。
输入非常给面子,haybale的所有信息都不需要存储,用后即弃。
dijk中,刚开始把所有点入队。
#include <bits/stdc++.h>
using namespace std;
vector<pair<int, int> > a[50020];
int n, m, k;
int d1[50020];
int d2[50020];
set<pair<int, int> > s;
void dijk(int *d) {
for (int i = 1; i <= n; i++) {
s.insert(make_pair(d[i], i));
}
while (s.size()) {
int u = s.begin() -> second;
s.erase(s.begin());
for (int i = 0; i < a[u].size(); i++) {
if (d[a[u][i].first] > d[u] + a[u][i].second) {
s.erase(make_pair(d[a[u][i].first], a[u][i].first));
d[a[u][i].first] = d[u] + a[u][i].second;
s.insert(make_pair(d[a[u][i].first], a[u][i].first));
}
}
}
}
int main() {
freopen("dining.in", "r", stdin);
freopen("dining.out", "w", stdout);
scanf("%d%d%d", &n, &m, &k);
for (int i = 0; i < m; i++) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
a[x].push_back(make_pair(y, z));
a[y].push_back(make_pair(x, z));
}
memset(d1, 0x3f, sizeof d1);
d1[n] = 0;
dijk(d1);
memset(d2, 0x3f, sizeof d2);
for (int i = 0; i < k; i++) {
int x, y;
scanf("%d%d", &x, &y);
d2[x] = d1[x] - y;
}
dijk(d2);
for (int i = 1; i < n; i++) {
printf("%dn", d1[i] >= d2[i]);
}
}[/hide]
[vc_row][vc_column][vc_btn title="USACO学术活动辅导课程推荐" color="primary" size="lg" align="center" button_block="true"][/vc_column][/vc_row][vc_row][vc_column][products columns="2" orderby="title" order="ASC" ids="730, 725"][/vc_column][/vc_row]
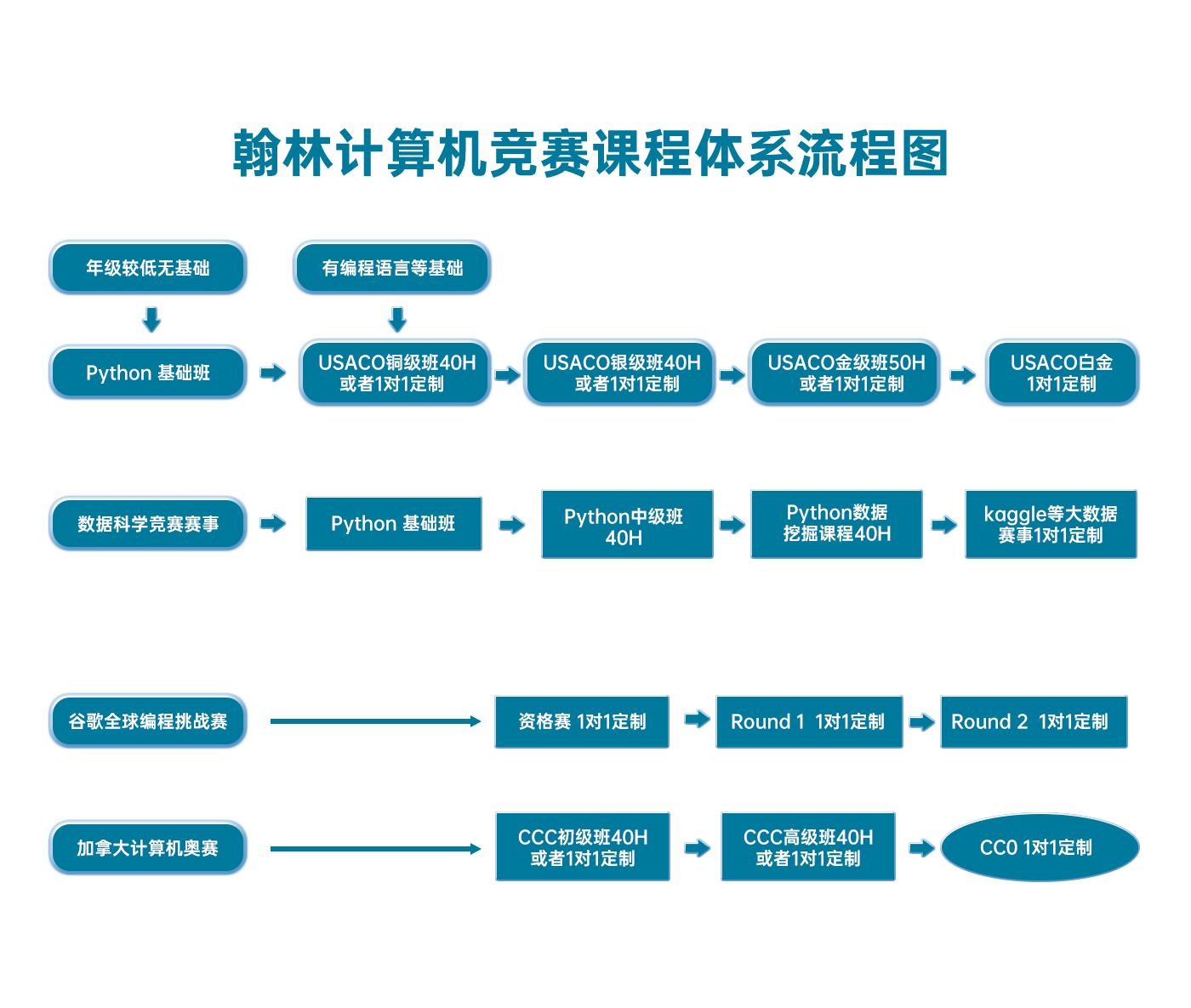
翰林USACO课程体系流程图

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1










