A-Level数学：相关变化率（Related Rates）解题思路

在ALevel数学关于微分的内容中，让很多学生都感到头疼的一类习题就是关于相关变化率（Related Rates）的问题，这一类问题经常会出现很多变量，让学生不知道该如何下手。今天我们来详细分析一下这类习题，找到快速解题的窍门。 

1我们先看一道例题：

Air is being pumped into a spherical balloon (see Figure 3.38) at a rate of 4.5 cubic feet per minute.Find the rate of change of the radius when the radius is 2 feet.

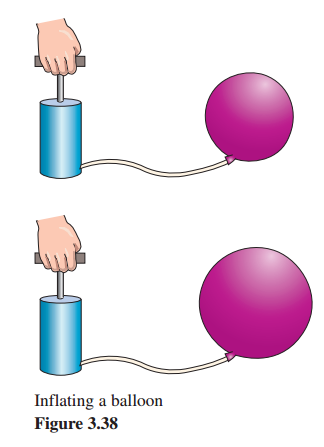
本题的意思是说：每分钟给气球打气的速度是4.5立方英尺每分钟，求当气球的半径正好是2英尺时的那一瞬间，气球半径增加的速率。

有生活常识的人都知道，如果体积增加的速率是恒定的，那么在气球比较小的时候，半径增加的会比较快，而当气球已经很大的时候，半径增加的就会比较缓慢了，所以虽然体积增加的速率恒定，但是半径增加的速率不是定值。那么该如何找到体积增加速率和半径增加速率的关系呢？

本题的关键在于，要找到已知条件和未知量，首先半径是2英尺，而本题中的每分钟充气的体积，实际上就是体积相对于时间的变化率，也就是dV/dt。本题要求的是半径增加的速率，其实也就是半径相对于时间的变化率：dR/dt。

对于本题，我们需要找到不带微分符号时，已知变量和未知变量的恒等关系，也就是体积V和R两个变量的关系，然后对时间t做微分，就能得到dR/dt的表达式。过程如下：

 所以针对related rates一类的问题，不管题目有多复杂，我们只需要找到两个相关变量的恒等关系，这类关系可以是面积或体积的恒等式，也可以是勾股定理，三角函数关系等不管变量如何变化，等式都保持相等的关系。最后再对时间t做微分，就能找到未知量的微分值了。

2那么看看下面这道题，你是否有思路了呢？

Find the rate of change in the angle of elevation of the camera shown in Figure 3.40 at 10 seconds after lift-off.

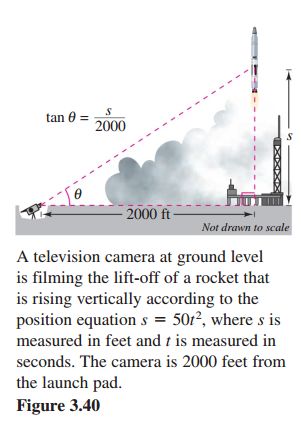
解题过程如下：