AMC12答题技巧及AMC12答题时间分配分享 2023AMC12考前冲刺

AMC12考试即将到来，时间紧迫，任务繁重。为了帮助大家高效备考，我们提供以下备考锦囊，涵盖了大部分考生关心的考前必备知识。不论你是否是AMC12考生，都值得仔细阅读。

考前明确事项

在考试前需要明确以下几个事项：

确定目标：明确自己的考试目标是什么？是进入AIME，争取1%的名次，还是发挥出自己的最佳水平就好？设定一个明确的目标可以帮助你更有动力和方向性地备考。

答题策略：为了实现自己的目标，需要确定一些答题策略。例如，决定要做到第几题，计划要做对多少道题目，是否留空一些题目，以及允许自己错几题等。这样的策略可以帮助你在考试中更有计划地进行答题。

时间分配：在考试中，合理的时间分配非常重要。确定每道题目的目标用时和最多允许用时，并留出一些时间来进行检查。这样可以避免在时间上过度耗费，确保能够完成整个考试。

强弱分析：了解自己的优势和劣势模块非常重要。是否有某些模块特别擅长？考虑是否优先做自己擅长的题目。同时，也要注意是否有一些模块比较薄弱。如果是，是否要先跳过自己薄弱的题目，以充分利用时间和提高得分率。

答题时间分配

确定自己的时间分配

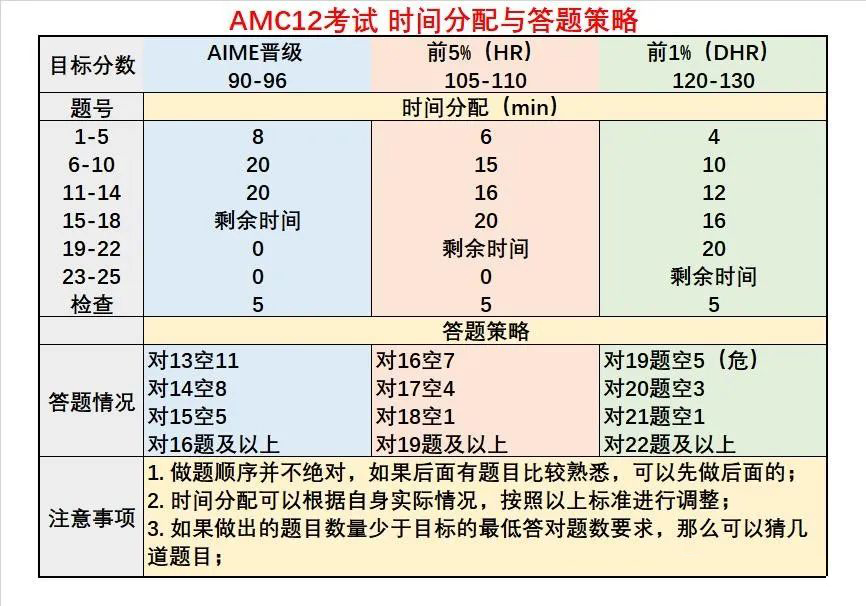
答题策略及顺序

根据自己的强弱情况，可以考虑调整答题顺序。以下是一些建议的答题策略：

均衡型：如果自己在不同模块上的水平相对均衡，可以按照题目顺序进行答题。控制好每道题目的时间，如果卡在一道题上时间过长，及时跳过，继续进行下一题。

模块回避型：如果自己在某一模块上明显薄弱（例如组合），可以先跳过这类题目，完成其他题目。如果还有时间，再回过头来解答这类题目。

模块优先型：如果自己在不同模块上的水平差别明显，可以根据自己的水平从高到低依次解答剩余题目。例如，如果几何是你最擅长的，可以先解答几何题目；如果组合是你最薄弱的，可以将其放在最后解答。

以下是一些重要的公式，需要在备考过程中进行记忆和熟悉：

代数：各函数的图像特征（二次、三角、指数、对数、绝对值、取整函数、复合函数、反函数、平移、伸缩、对称等图像变换），三角恒等变换公式，复数相关公式，对数运算公式，递推数列求解通项方法，均值不等式，高次方程韦达定理，坐标系中距离公式（点-点、点-直线、直线-直线），直线夹角公式，鞋带定理。

几何：常见面积和体积公式，勾股定理，角平分线定理，正余弦定理，圆幂计算公式，三角形center的相关性质，圆内接四边形的相关性质，托勒密定理，Stewart定理。

数论：因式分解公式，因数相关公式（个数、和、乘积），进制转化公式，同余计算法则与同余方程解法，中国剩余定理。

组合：插板法公式，二项式定理，容斥原理公式。

AMC10及AMC12有任何疑问，请咨询【翰林提供报名服务】

扫码免费获取历年真题（备战AMC8请扫码）

请在备考过程中逐渐熟悉和掌握这些公式，并在解题时灵活运用。祝你考试顺利！