- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
USACO十一算法camp小结-Day1
Day1 总结
单独约谈各位学员,了解大家的基础,编程语言学习历史,和比USACO的计划
根据各位同学的语言基础调整课程形式,降低课程难度
快速了解OI赛事的特点
练习2018USACO2月铜题1-3题(首次中文题),熟悉USACO赛事的难度,比赛形式
答题通过情况(AC)
铜1 全员通过
铜2 黄常麟 韩子键 余铁琳 陈晟劢 石博闻 徐常捷
铜3 余铁琳 孔伯铭 石博闻 Daniel
银1 石博闻 Daniel 孔伯铭(部分)
银2 石博闻
6.下午讲解算法:倍增,排序,贪心,欧几里德算法等 算法详细内容及参考资料总结:
7. 晚餐全体人员聚餐
8.聚餐后部分学员继续攻克代码,直到现在(晚上10:00pm)
毕克导师课程讲稿(含大量参考链接内容,信息量大,建议收藏)
1自我介绍
毕克
2010 ∼ 2013,⽯家庄⼆中。
NOI 2012 ⾦牌。
2013 ∼ 2017,清华⼤学。
5 次区域赛/EC-FINAL ⾦牌。
没去过 IOI,也没去过 ACM World Final。现在在⾹港上学(划⽔)。
三⼤爱好:⽐赛,出题,讲课。
QQ:751723392, Email:wwwwodddd@gmail.com
2Competitive programming
算法⽐赛 是⼀种⽐较成熟的⽐赛形式。
简单来说,就是按照题⽬要求,读取指定格式的输⼊,经过⼀些处理,按照指定格式输出。最简单的输出⽐较就是逐字节⽐较,也就是输出必须和答案⼀模⼀样,才算正确;当然也有
的题⽬是 Special Judge,也就是只要满⾜⼀定条件即可。
⼀般情况下,除了反作弊的需要之外,不关注代码如何实现的。
⾮常客观。⽅便⾃⼰调试。
增加⼀个参赛选⼿,额外代价很低。
对于⾼中阶段
中国的⽐赛有 NOIP 和 NOI。美国的⽐赛有 USACO。
2.1 学习的意义
⾼中阶段学习 OI,可以保送⼤学。
⼤学阶段学习 ACM,可以获得部分公司的青睐。(然后也可以⽐赛,出题,讲课,⾛上经济独⽴之路。)
3评测结果
3.1AC (Accepted)
表⽰通过。
3.2WA (Wrong Answer)
表⽰程序成功运⾏,但是输出和标准答案不⼀样,或者是没有通过 Special Judge 的检测。
3.3 CE (Compile Error)
编译失败,需要注意在线的编译器和你使⽤的编译器不⼀定⼀样,有⾮常多的原因会导致本机可以编辑,提交得到 CE。
3.4RE (Runtime Error)
表⽰程序崩溃。
有三种可能,数组越界,爆栈,除以 0。
3.5 TLE (Time Limit Exceeded)
程序使⽤的时间过长,没有顺利运⾏完成。
有两种可能,算法太慢,或者是出现了死循环。
3.6MLE (Memory Limit Exceeded)
程序使⽤的空间过⼤,没有顺利运⾏完成。
3.7OLE (Output Limit Exceeded)
程序不停的输出,于是被结束了。
4 常见错误
4.1不要输出任何多余字符
不要输出任何多余字符,提⽰语句,或者是调试语句。
⽐如不要输出 please input an integer: 或者 the answer is。
4.2程序要顺利结束
在上古时期写程序,如果什么都不加,程序编译运⾏后会⼀闪⽽过。所以常常在结尾加上 system("pause") 或者 while(1);
4.3看清题目数据范围
除了刚开始学编程,绝⼤多数题⽬都需要⼀定优化,⼀定要考虑在最坏的情况下程序能否运⾏。
复杂度 (Complexity)
5.1时间复杂度
我们特别关注运⾏时间与输⼊规模的关系。
对于运⾏时间,我们⼀般考虑基本操作的次数。
⽐如可以认为⼀次运算是基本操作,⼀次赋值或者⽐较也是基本操作。
特别的,⼀般情况下并不关⼼常数问题,⽐如 a += b 可以看做⼀次基本操作,也可以看做两次基本操作。
这就是⼤家常常说的 O(n),O(n2) 的意思。
5.2 空间复杂度
对于算法⽐赛来说,不需要特别关注这个内容。
⼀个 int 是 4 字节,106 个 int 是 4MB,其他的空间⼤⼩以此类推。需要注意的是,即使什么都不写,也会占⽤⼏百 KB 的空间。
USACO 比赛介绍
12 ⽉,1 ⽉,2 ⽉,和⼀场 US Open。
每次分为四个级别:Bronze, Silver, Gold, Platinum。
每次在 72 ⼩时中选择 4 ⼩时参加(不要问我如何防⽌作弊) 刚开始只能参加 Bronze,达到⼀定分数之后可以参加下⼀级。
⽐赛实时返回结果。
不要抄袭,⽐赛中不要进⾏代码上的交流。
不能打表,你不能本机运算出所有输⼊的答案,然后打表提交。(当然我觉得打表主要和出题⽔平有关)
7C++
学会查⽂档。
中⽂⽂档
英⽂⽂档
另⼀份英⽂⽂档
7.1 变量
各个类型的变量是有范围的,具体来说跟⼆进制有关。反码
补码
⼤家注意浮点数 double 的存储⽅式,类似科学计数法
IEEE 754
7.2运算符
注意运算优先级,尤其是位运算部分。注意异或和 power。
注意短路运算 与位运算的区别。
注意单⽬运算符负号,与减法的区别注意运算中类型的强制转换
7.3判断和循环
没什么好讲的,相信⼤家已经掌握了。
STL
我认为 C++ 中⽐较有⽤的东西:
next_permutation sort
set map
priority_queue
7.5 信息学
信息学不需要 C++ 中华丽的特性。信息学写的代码基本是⼀次性的。
C++ 可以提供底层和顶层的书写⽅式。
⽐ Pascal 便于书写。
⽐ Python 效率⾼。
与之类似的还有 Java 语⾔,不过效率稍低。
信息学不关⼼⽤户体验,只需要输出应该输出的即可。时间复杂度是影响程序速度的重要指标。
8Java
Java 是⼀个完全⾯向对象的语⾔基本语法和 C++ ⾮常相似但是要注意以下的不同。
库函数的区别⽐如排序,等函数,Java 的⽤法和 C++ 完全不同。还有⼀些容器,⽐如 Map Set 等也很不相同。
另外 Java 中对于对象(结构体)都是传引⽤,⽽不是传值。这也是值得注意的⼀点。
9Python
9.1交互式
Python 的交互功能⾮常好⽤,推荐每个⼈都学习使⽤。
并且 Python ⽀持计算⾼精度,可以⽤来当进阶版的计算器。
9.2 变量
变量不需要声明,不需要明确类型。
9.3 运行速度
Python 的运⾏速度⾮常慢,并且不容易被估计。并不建议在需要优化效率的情况下使⽤。
Python 2 和 Python 3
Linux 计算机⼀般默认安装 Python 2,所以建议学习 Python 2。当然如果你已经会了 Python 3,也不⽤换,了解 Python2 和 3 的差别即可。
10USACO 2017
⼀共有四场⽐赛。难度逐渐增加。
从 2018 February 开始,题⽬描述开始有了简体中⽂版。
11USACO 2017 December Contest, Bronze, Problem 1. Blocked Billboard
11.1题目背景
Blocked Billboard
11.2题目大意
求矩形⾯积交
11.3 题目解法
求矩形⾯积交
12USACO 2017 December Contest, Bronze, Problem 2. The Bovine Shuffle
12.1题目背景
The Bovine Shuffle
12.2题目大意
数组的嵌套使⽤。
12.3题目解法
数组的嵌套使⽤ s[a[a[a[i]]]]。
13USACO 2017 December Contest, Bronze, Problem 3. Milk Measurement
13.1题目背景
Milk Measurement
13.2题目大意
模拟,三个数字求最⼤值。
13.3题目解法
模拟,三个数字求最⼤值。
14USACO 2018 January Contest, Bronze, Problem 1. Blocked Billboard II
14.1题目背景
Blocked Billboard II
14.2题目大意
分类讨论,矩形⾯积交。
14.3 题目解法
分类讨论,矩形⾯积交。
15USACO 2018 January Contest, Bronze, Problem 2. Life- guards
15.1 题目背景
Lifeguards
15.2题目大意
枚举,模拟。
15.3 题目解法
枚举,模拟。
16 USACO 2018 January Contest, Bronze, Problem 3. Out of Place
16.1题目背景
Out of Place
16.2题目大意
⼀个有序的数列中,插⼊了⼀个数字。
问⾄少多少次交换,可以使得这个序列再次变得有序。初始的序列中可能有相同的数字。
16.3题目解法
排序之后,检查有多少个数字发⽣了变化。如果没有,答案是 0。
如果有 k 个,那么需要 k − 1 次交换。
17USACO 2018 February Contest, Bronze, Problem 1. Teleportation
17.1题目背景
Teleportation
17.2题目大意
数轴上两点之间的距离。
17.3 题目解法
数轴上两点之间的距离。
18 USACO 2018 February Contest, Bronze, Problem 2. Hoofball
18.1题目背景
Hoofball
18.2 题目大意
英语题
”the cow farthest to the left among these” 是指最左边的,⽽不是指距离左边最远的。
18.3 题目解法
对于⼀头⽜来说,如果没⼈给他球,那么 John 必须给他。
特别的,如果对于孤⽴的 2 头⽜,他们互相传,那么 John 也必须给其中⼀个⼈。
19 USACO 2018 February Contest, Bronze, Problem 3. Taming the Herd
19.1 题目背景
Taming the Herd
19.2 题目大意
题目解法
如果⼀天是 x(x > 0),那么前⼀天必须是 x − 1。如果⼀天需要是不同的数值,那么⽆解。
第⼀天必须是 0。
在满⾜以上条件的情况下,所有 −1 都可以变为 0 或变为之前的数字加⼀。
20USACO 2018 US Open Contest, Bronze, Problem 1. Team Tic Tac Toe
20.1 题目背景
Team Tic Tac Toe
20.2 题目大意
阅读理解题
20.3 题目解法
选出来的 2 个字母⽆序。
必须是存在⼀⾏,两个都有才可以。
21USACO 2018 US Open Contest, Bronze, Problem 2. Milking Order
21.1 题目背景
Milking Order
21.2题目大意
题目解法
考虑如何判断⽆解,如果可以判断⽆解,枚举 1 ⽜的位置,然后判断是否有解即可。
22 USACO 2018 US Open Contest, Bronze, Problem 3. Family Tree
22.1 题目背景
Family Tree
22.2 题目大意
题目解法
模拟
倍增
⽤处最⼴的就是快速幂
快速幂可以处理所有满⾜结合律的东西。
24 Luogu P1226
24.1 题目背景
24.2 题目大意
快速幂
24.3 题目解法
快速幂
见多识⼴的同学可能觉得这个题可以⽤欧拉定理抢救⼀下。并没有必要。
排序 (sort)
3 个 O(n2) 排序。
3 个 O(n log n) 排序。
快速排序,最常⽤。
归并排序,可以算逆序对。
堆排序,只需要 O(1) 的额外空间。
贪心算法 (Greedy algorithm)
有很多⾮常好的贪⼼题⽬。
但是因为需要的知识过于艰深,所以只好先挑⼀些简单的。
27 Luogu P1007
27.1 题目背景
27.2 题目大意
题目解法
假设相遇之后不是同时调头,⽽是互相穿过。
28 Luogu P1208
28.1 题目背景
P1208 [USACO1.3] 混合⽜奶 Mixing Milk
28.2 题目大意
题目解法
按价格排序,然后贪⼼。
29 Luogu P1223
29.1 题目背景
29.2 题目大意
题目解法
对于第 i 个⼈,如果他倒数第 j 个接⽔,那么对全局的贡献是 jti。所以接⽔快的,应该先接⽔。
30 bzoj 2563
30.1 题目背景
30.2 题目大意
题目分析
贪⼼!
递归
递归本质上并不需要存在,只是为了程序容易实现。
⼀些例⼦:阶乘,Fibonacci 数。递推式,终⽌条件。
32 欧几里得算法
计算最⼤公约数:欧⼏⾥得算法
33 搜索
枚举所有的状态。
33.1 枚举所有子集
枚举⼤⼩为 n 的集合的所有⼦集。
⽤位运算。
枚举⼦集的⼦集。
33.2 枚举固定大小的子集
枚举⼤⼩为 n 的集合的所有⼤⼩为 m 的⼦集。
next permutation
似乎有⼀种⽤位运算的⽅法,但是我记不得了。
33.3 枚举所有排列
枚举 1 到 n 的所有排列。深搜。
next permutation。
值得注意的是。next permutation 处理有重复元素的时候,不会把相同的排列⽣成 2 次。
33.4 其他
但是在很多情况下,还是需要⽤深搜的
34 深度优先搜索(搜索)
⽤栈。
但是因为有递归,这个栈,并不需要你来实现。
⼀般适⽤于:找到任意⼀个解,或者找到所有解。或者是状态⾮常⼤,不适合深度优先搜索。
34.1 细节
核⼼在于状态更新与复原。
有的时候还需要标记 visited 数组,表⽰这个状态被搜过了。
35 剪枝
遇到⼀些不合法的状态,可以直接剪枝,⽽不是等到枚举到最后再剪枝。
36 广度优先搜索(搜索)
⽤队列。
需要⾃⼰实现队列。
⼀般适⽤于:找到步数最⼩的解。 注意随着步数增加,状态指数增长。
36.1 细节
核⼼在于把状态压缩,要能存下。
有的时候还需要标记 visited 数组,表⽰这个状态被搜过了。
37 双向广度优先搜索
从最开始的状态和最后的状态⼀起搜索。
这样只需要最⼩步数的⼀半,就可以搜出答案了。
随着步数增加,状态指数增长,步数减少⼀半,状态减少明显!
38 IDA*
每个状态很⼤,并不能⼴搜? 要求最⼩步数?
枚举最⼩步数,然后深搜判断有没有解。
每多⼀层,多花费的时间是上⼀层的数倍,上⼀层的时间可以忽略。
39 Luogu P1219
39.1 题目背景
39.2 题目大意
经典问题⼋皇后。
39.3 题目解法
直接深搜即可。
40 Luogu P1312
40.1 题目背景
40.2 题目大意
NOIP 2011 的⼀个搜索模拟题。
40.3 题目解法
41 bzoj 1501
41.1 题目背景
41.2 题目大意
暴⼒搜索。
41.3 题目分析
需要努⼒写代码。
翰林USACO课程体系流程图
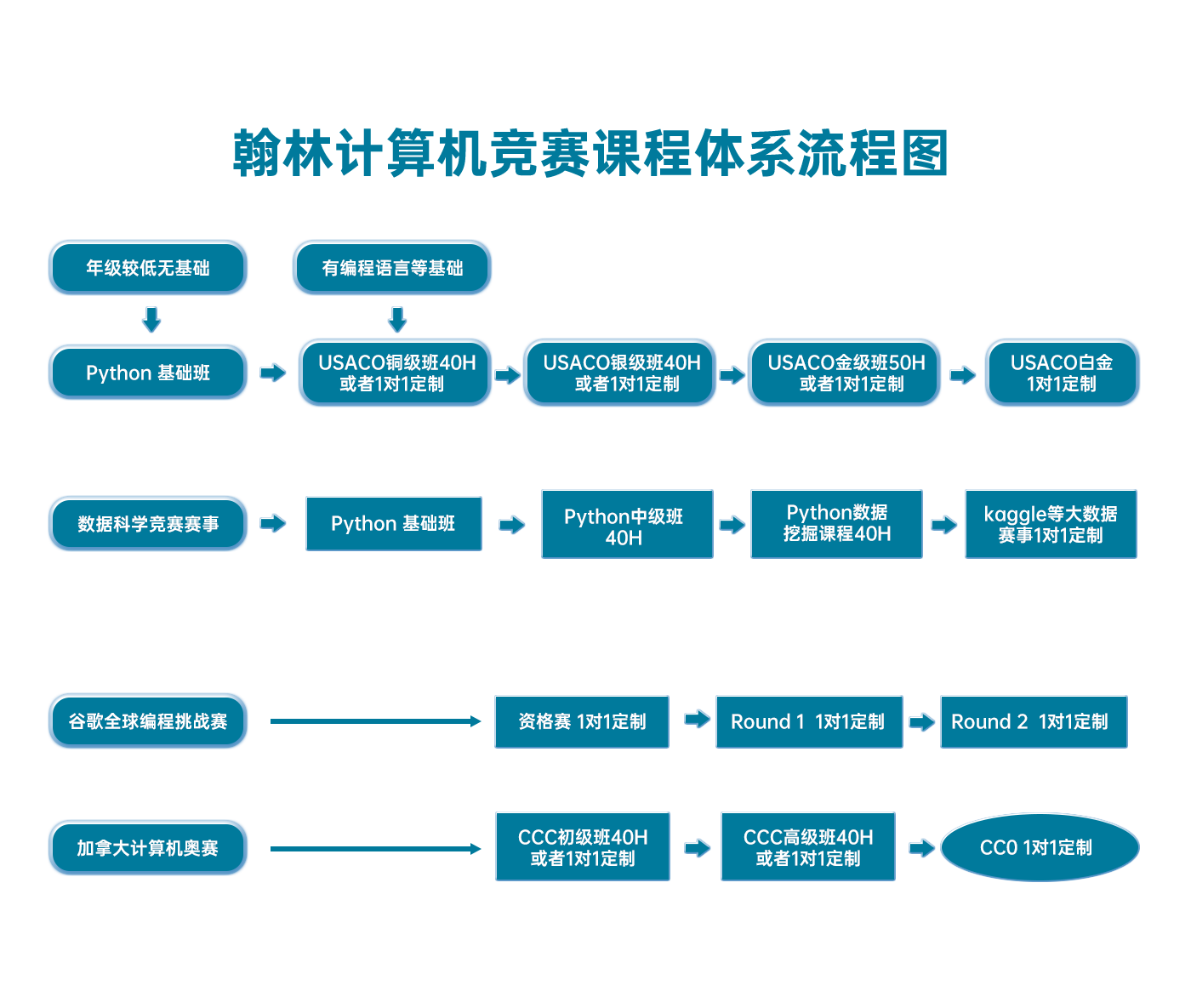

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









