2023HiMCM新赛季报名正式开启！附HiMCM数模竞赛流程解析

当提到广受影响力的数学学术活动时，许多人会立刻想到AMC、AIME、PUMaC等学术活动，但这些学术活动有一个共同点——都是笔试答题。那么，是否存在一种形式新颖、更具挑战性的数学学术活动呢？

事实上，确实存在这样一种学术活动！

HiMCM是一项独特的数学学术活动，它涉及团队赛、建模和提交论文。不仅需要选手具备编程技巧，更注重数学、逻辑思维和论文写作能力。

同时，该学术活动借鉴了美国大学生数学建模学术活动的模式，并结合了中学生的特点进行设计。它是由美国数学及其应用联合会（COMAP）主办的一项国际性数学学术活动活动。

2023HiMCM赛事基本信息

适合人群

对应用数学感兴趣、并有一定的数学基础，未来专业为数学、工程、计算机、商科的学生。适合在初三到高三，希望挑战自我，冲击世界知名大学的学生。

队伍人数

由1-4名在校高中生组成，所有队员必须来自同一所学校，配备一位指导老师。

开放报名

2023年9月29日

注册截止日期

美国东部时间2023年11月1日星期三下午2:00

比赛窗口打开

美国东部时间2023年11月1日星期三下午3:01

比赛窗口关闭

美国东部标准时间2023年11月14日星期二晚上8:00

解决方案报告截止日期

美国东部标准时间2023年11月14日星期二晚上9:00

比赛结果公布时间

2024年2月1日或之前公布

快来翰林寻找志同道合的伙伴吧！组队信息可咨询顾问老师~

数学建模的主要过程

在A First Course in Mathematical Modeling这本教材中出现的数学建模五步法，应该是大家耳熟能详的，这里给大家分享一下：

Part.1第一步

提出问题

Part.2第二步

选择建模方法

Part.3第三步

推导模型的公式：

1、 将第一步中得到的问题重新表达成第二步选定的建模方法所需要的形式.

2、 你可能需要将第一步中的-些变量名改成与第二步所用的记号一致.

3、 记下任何补充假设，这些假设是为了使在第一步中描述的问题与第二步中选定的数学结构相适应而做出的。

Part.4第四步

求解模型：

1、 将第二步中所选方法应用于第三步得到的表达式.

2、 注意你的数学推导，检查是否有错误，你的答案是否有意义．

3、 采用适当的技术．计算机代数系统，图形，数值计算的软件等都能扩大你能解决问题的范围，并能减少计算错误．

Part.5第五步

回答问题用非技术性的语言将第四步的结果重新表述。

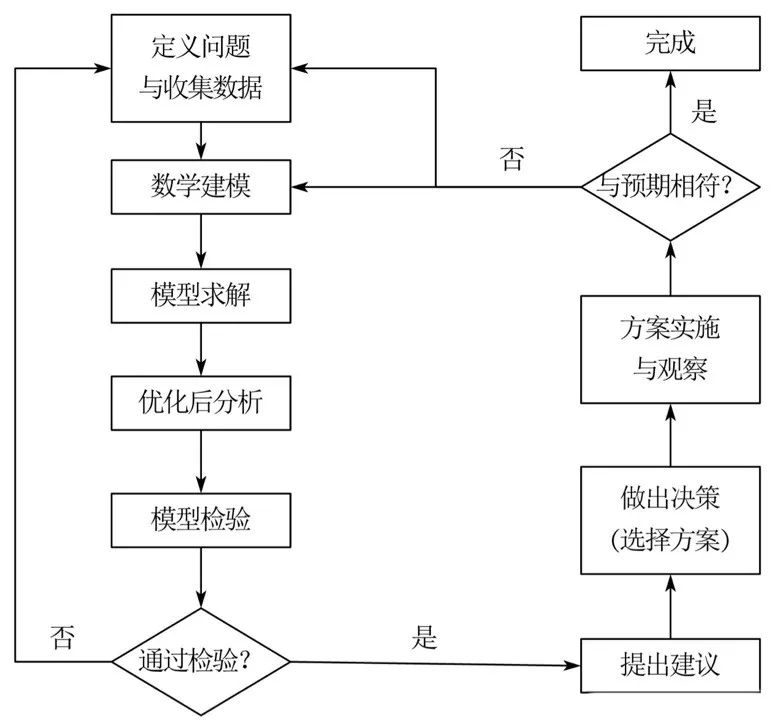
这个流程图便是基于模型解决问题的一般流程，数学建模五步法与其相比更加精简，更适合在数学建模学术活动中应用，而该流程在实际生活中也更具指导意义！