2006COMC加拿大数学公开赛真题答案免费下载

历年 Canadian Open Mathematics Challenge加拿大数学公开赛

真题与答案下载

翰林国际教育全网首发

力争超快速发布最全资料

助你在升学路上一帆风顺

为你

千千万万遍

2006 COMC真题答案免费下载

共计2.5小时考试时间

此套试卷由两部分题目组成

Part A共8题，每题5分

Part B共4题，每题10分

共计12题，满分80分

不可使用任何计算器

完整版下载链接见文末

部分真题预览：

Part A Solutions:

A6)Two Solutions:

Solution 1: Since 0 < n < 10⁷, then n is a positive integer with fewer than 8 digits.
Since n is divisible by 6, then n is even. Since each digit of n is either 1 or 0, then n must end with a 0.
Since n is divisible by 6, then n is divisible by 3, so n has the sum of its digits divisible by 3.
Since each digit of n is 0 or 1 and n has at most 6 non-zero digits, then the sum of the digits of n must be 3 or 6 (that is, n contains either 3 or 6 digits equal to 1).
Since n has at most 7 digits, we can write n in terms of its digits as abcdef0, where each of a, b, c, d, e, f can be 0 or 1. (We allow n to begin with a 0 in this representation.)
If n contains 6 digits equal to 1, then there is no choice in where the 1’s are placed so n = 1111110.
If n contains 3 digits equal to 1, then 3 of the 6 digits a through f are 1 (and the other 3 are 0). The number of such possibilities is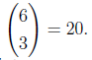
Therefore, there are 20 + 1 = 21 such integers n.

Part B Solutions:

B1)

1. Since the average of 3 and 19 is 1/2(3 + 19) = 11, then 11 goes between the 3 and 19. The number which goes below 8 is the number whose average with 3 is 8, so 13 goes below 8.
   The average of 13 and 19, or 16, goes in the middle square.
   The number which goes to the right of the 16 is the number whose average with 8 is 16, or 24.
   The number which goes below 24 is the number whose average with 19 is 24, or 29.
   The number which goes between 13 and 29 is their average, which is 21.
   Therefore, the completed grid is .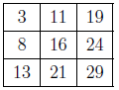
   (We can check that each line obeys Piotr’s Principle.)
   Note:There are other orders in which the squares can be filled.
2. Note: When we have the three numbers a, X, b on a line, then X is the average of a and b, so X = 1/2 (a + b).
   When we have the three numbers a, b, X on a line, then b is the average of a and X, so b = 1/2 (a + X) or 2b = a + X or X = 2b − a.
   These facts will be useful as we solve (b) and (c).
   Two Solutions:
   1. Solution 1:The average of 5 and 23 is 1/2(5+23) = 14, which goes in the square between the 5 and 23. Since the average of the numbers above and below the 5 equals 5, then their sum is 2(5) = 10. (Note that we do not need to know the actual numbers, only their sum.)
      Similarly, the sum of the numbers above and below the 14 is 2(14) = 28 and the sum of the numbers above and below the 23 is 2(23) = 46.
      Therefore, the sum of the numbers in the whole grid is 5 + 10 + 14 + 28 + 23 + 46 = 126.
3. The centre square is the average of 9 and y and is also the average of x and 20.
   Comparing these facts, 1/2(9 + y) = 1/2 (x + 20) or 9 + y = x + 20 or x − y = −11.
   The number in the top right corner gives an average of 7 when combined with x (so equals 2(7) − x = 14 − x) and gives an average of y when combined with 20 (so equals 2y − 20).
   Therefore, 14 − x = 2y − 20 or x + 2y = 34.
   Subtracting the first equation from the second, we obtain 3y = 45 or y = 15.
   Substituting back into the first equation, we obtain x = 4.
   We check by completing the grid. Starting with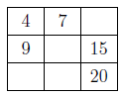 gives, after some work, 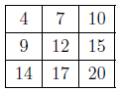, which does obey Piotr’s Principle. Therefore, x = 4 and y = 15.

完整版真题资料可以底部二维码免费领取↓↓↓